Tag Archives: Wall-E3

St Micro VL53L5CX Study – Single Module Parallel Detection?

Posted 15 January 2023

I currently use two 3-element arrays of ST Micro’s VL53L0X ‘time of flight’ distance sensors to determine my robot’s orientation with respect to a nearby wall. In a reply to a recent post of mine on the ST Micro Forum, St Micro guru John Kvam suggested that a single VL53L5CX sensor might take the place of all three VL53L0X’s – wow!

So, I’m currently at a stopping place on my mainline robot work (managed to kill a Teensy 3.5, and new ones are a few days out), I decided to take some time to study how the VL53L5CX module performs in detecting the parallel orientation condition.

John was kind enough to send me some experimental code – albeit with the warning that ‘some study would be required’ to see how it all works, so I’ll be working my way through the example code while also looking through the VL53L5CX datasheet.

I started this adventure by downloading the Sparkfun VL53L5CX library and looking at some of the examples. I was going to buy a couple of the SparkFun breakout boards as I like supporting their library development, but then I saw that I was going to have to pay about $11 (about 1/3 the cost of a single module) just for shipping! Now I know I’ve lost a mental step or two over the last few decades, but even I know that shipping a postage-stamp sized module can be accomplished via USPS for a dollar or two at the most, so I have some issues with a 10X profit margin just for shipping. Talk about ‘hidden fees’! So instead I purchased ST Micro’s eval kit (which contains 2ea modules) from DigiKey for about the price of one Sparkfun module, and shipping was about 1/4 the Sparkfun price.

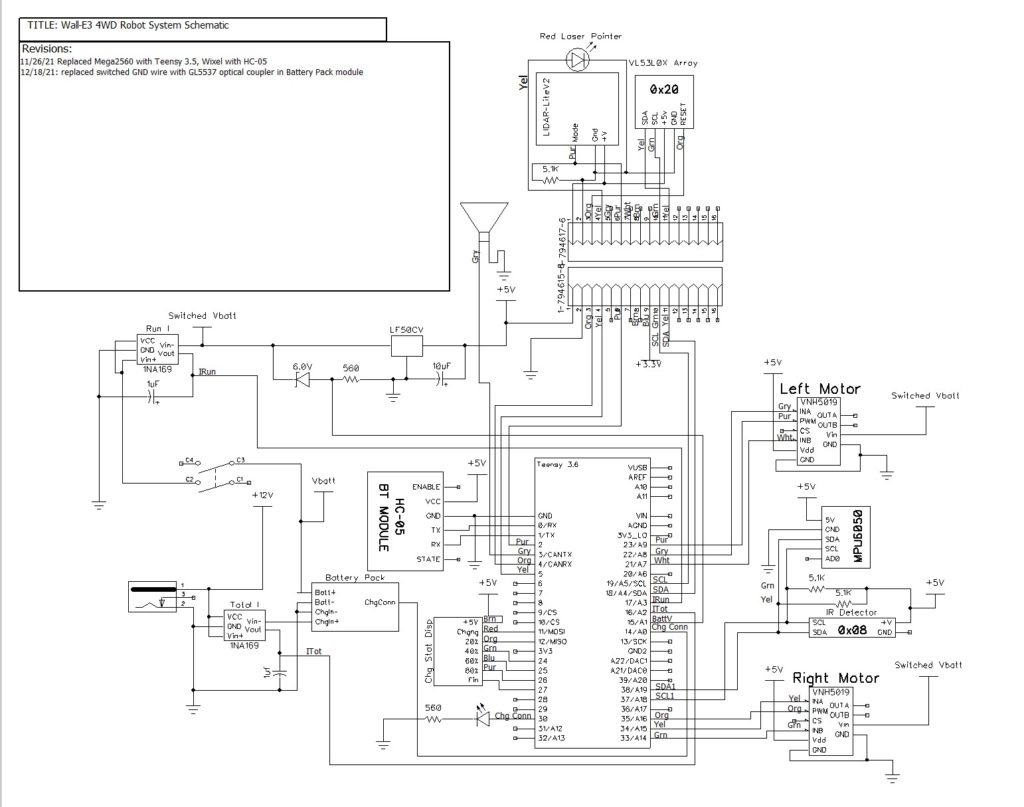
After receiving the modules, I hooked it up to a Teensy 3.5 as shown below. I wasn’t able to find any information about how to wire this unit to an Arduino (ST’s information assumes you have a NUCLEO board), so I had to kind of piece information together from multiple sources. I used Sparkfun’s schematic (I used 51K instead of 47K resistors) and connected PWREN (power enable) to 3.3V via a 51K.

ST Micro eval board for VL53L5CX ToF distance sensor

Then I loaded Sparkfun’s Example1 code, which simply prints out the values from all 64 zones in a timed loop. Here is some representative output:

	222	215	207	198	196	192	189	186
	204	197	190	184	183	177	175	171
	190	184	179	175	171	169	167	163
	175	171	168	163	163	159	157	150
	167	165	160	158	156	152	149	144
	155	155	151	148	145	145	140	133
	147	144	143	141	139	136	132	129
	140	135	135	131	130	126	125	123

	706	214	203	201	195	190	189	188
	206	194	191	184	184	177	174	172
	190	182	179	173	170	169	165	162
	179	171	168	163	162	158	157	151
	167	162	160	155	155	151	147	145
	157	154	153	145	145	143	140	134
	146	145	143	142	137	136	129	128
	141	136	134	132	129	124	125	121

	511	217	207	201	193	193	189	187
	205	197	192	183	183	179	175	172
	187	184	180	176	171	167	168	164
	176	172	169	163	161	158	155	150
	167	164	162	157	153	153	147	144
	157	153	152	146	146	139	140	134
	148	143	143	142	138	135	131	128
	142	137	135	131	130	126	124	123

	584	215	206	201	198	193	189	189
	206	193	189	182	182	179	174	170
	189	183	177	175	171	168	166	163
	177	172	167	165	163	159	155	150
	167	164	160	155	154	151	148	145
	156	155	150	146	146	142	140	132
	148	144	144	140	136	133	131	128
	142	136	134	134	129	125	126	122

222 215 207 198 196 192 189 186

204 197 190 184 183 177 175 171

190 184 179 175 171 169 167 163

175 171 168 163 163 159 157 150

167 165 160 158 156 152 149 144

155 155 151 148 145 145 140 133

147 144 143 141 139 136 132 129

140 135 135 131 130 126 125 123

706 214 203 201 195 190 189 188

206 194 191 184 184 177 174 172

190 182 179 173 170 169 165 162

179 171 168 163 162 158 157 151

167 162 160 155 155 151 147 145

157 154 153 145 145 143 140 134

146 145 143 142 137 136 129 128

141 136 134 132 129 124 125 121

511 217 207 201 193 193 189 187

205 197 192 183 183 179 175 172

187 184 180 176 171 167 168 164

176 172 169 163 161 158 155 150

167 164 162 157 153 153 147 144

157 153 152 146 146 139 140 134

148 143 143 142 138 135 131 128

142 137 135 131 130 126 124 123

584 215 206 201 198 193 189 189

206 193 189 182 182 179 174 170

189 183 177 175 171 168 166 163

177 172 167 165 163 159 155 150

167 164 160 155 154 151 148 145

156 155 150 146 146 142 140 132

148 144 144 140 136 133 131 128

142 136 134 134 129 125 126 122

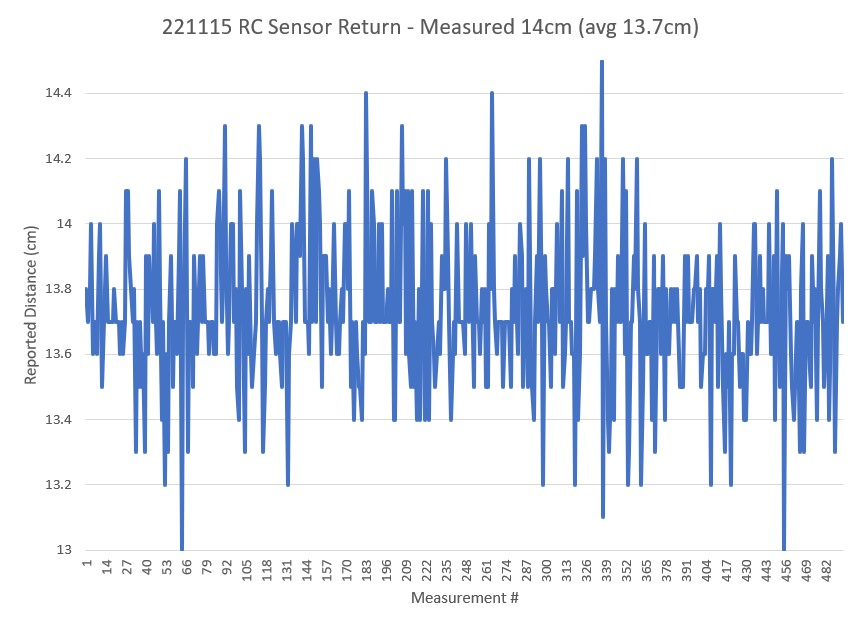
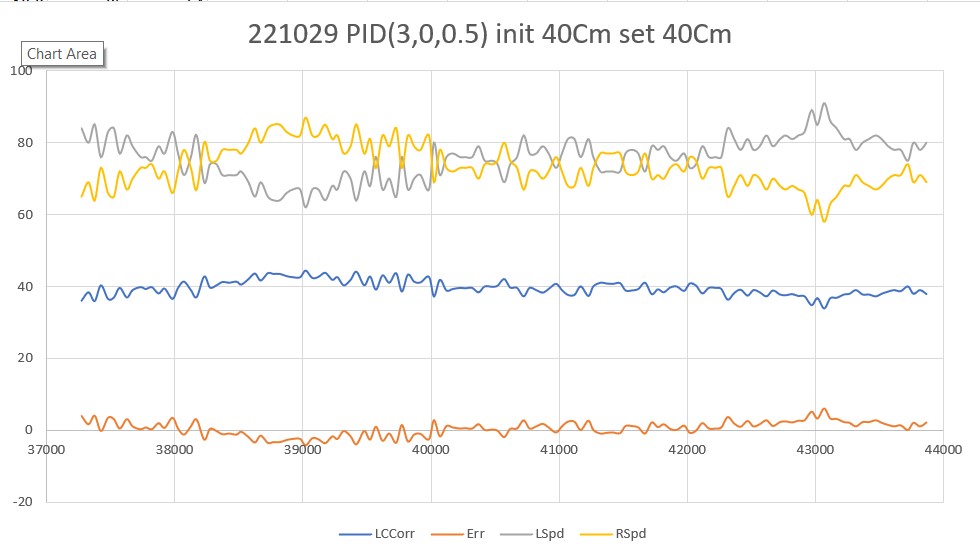
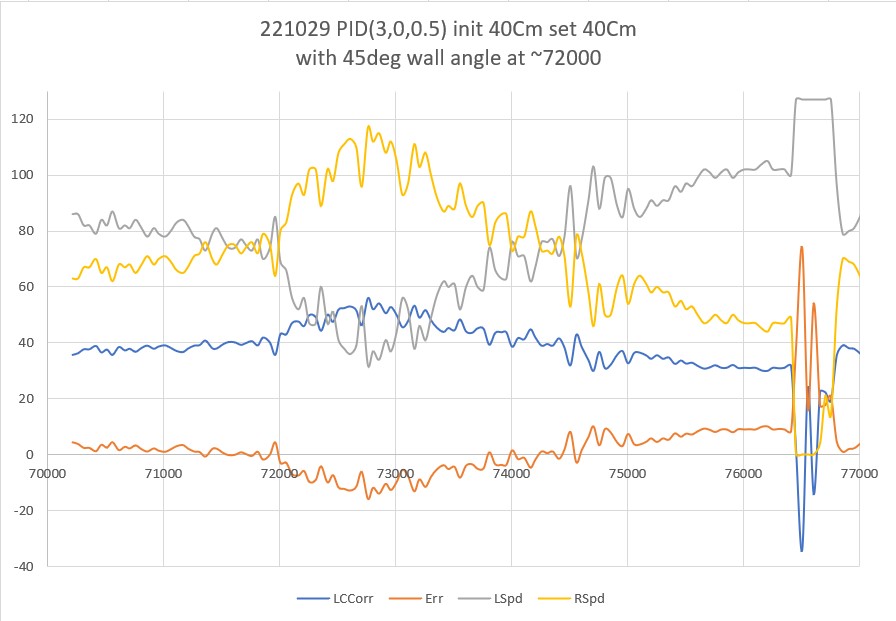
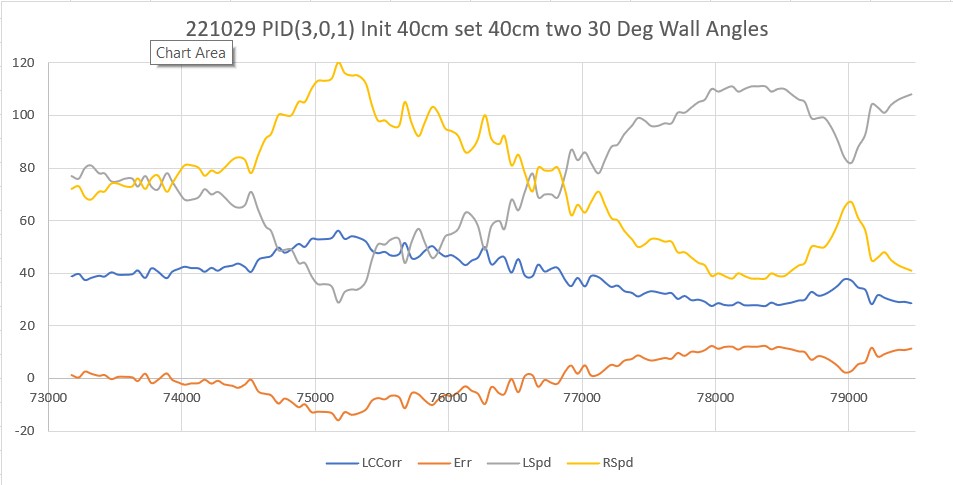
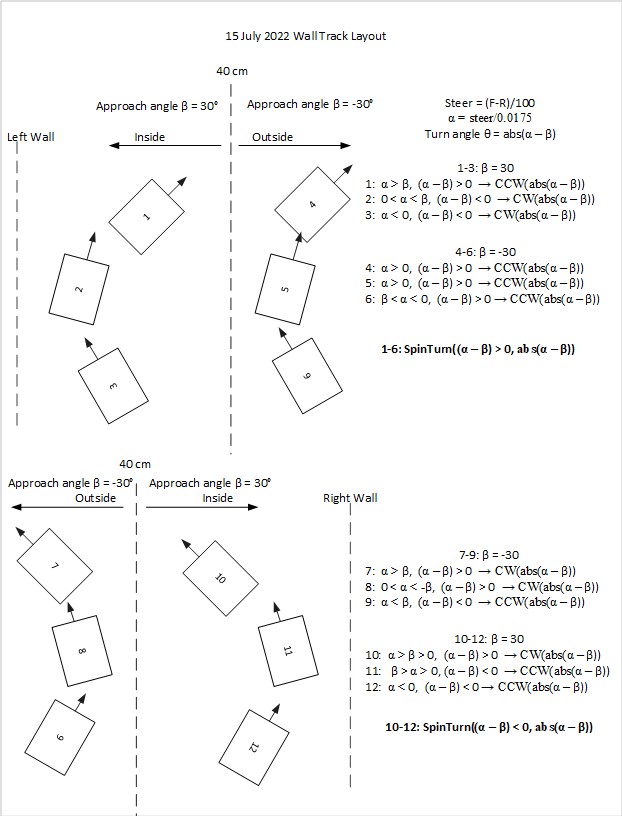
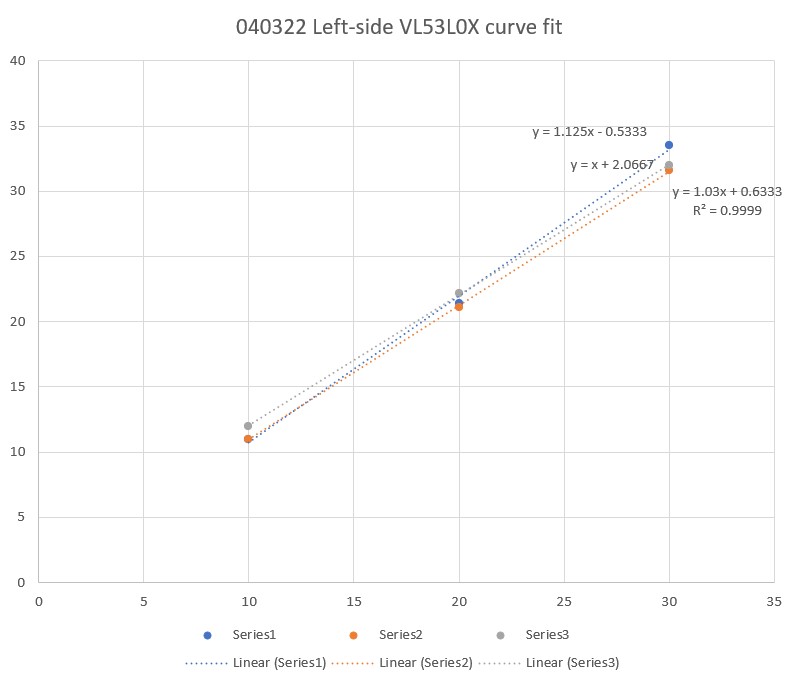
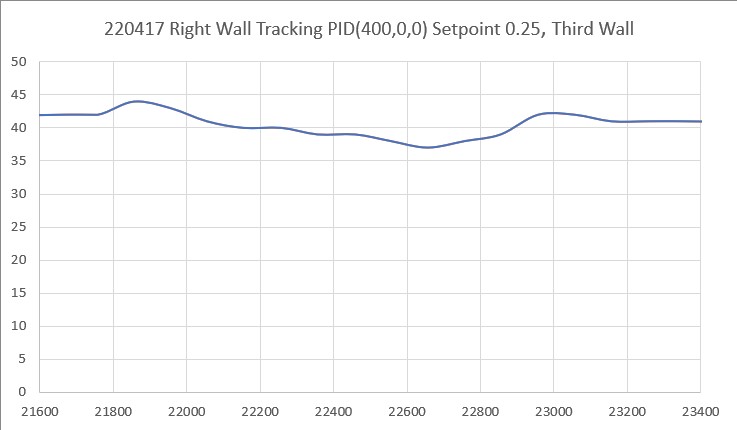
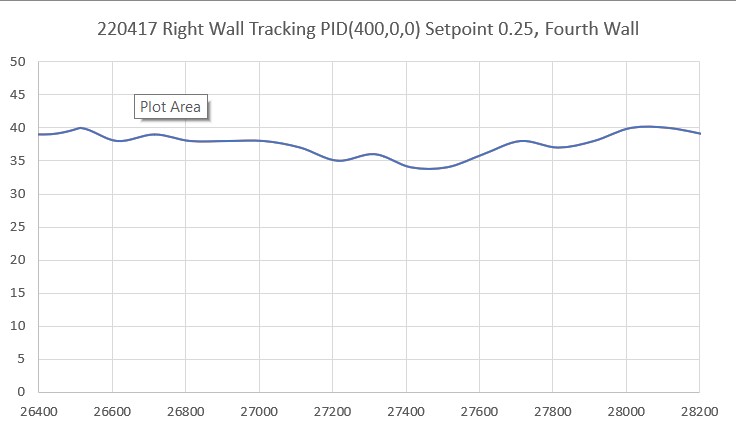
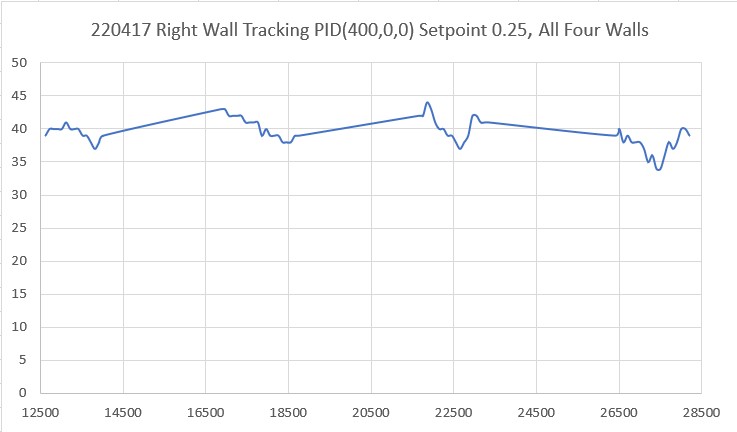
Then I set up an experiment with a nice white planar surface (the shoebox my recent B-ball shoes came in) at a distance of about 16cm, and observed the output for +30º, 0º (parallel), and -30º orientation conditions, as shown in the plots and photos below:

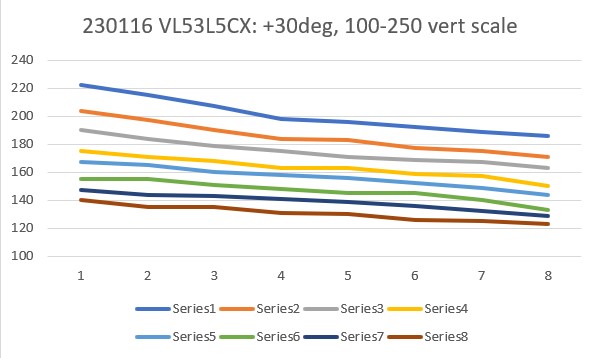
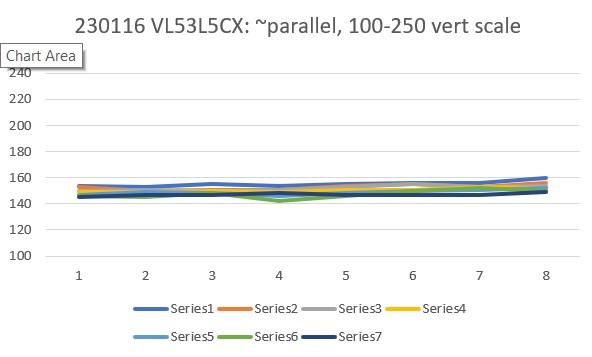
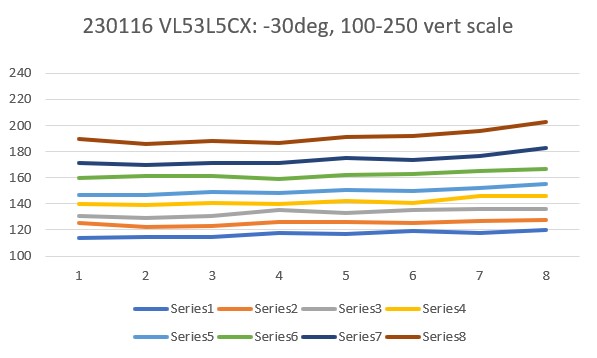
For comparison purposes, all three plots above were plotted on the same scale (100-250). Looking at the blue (Series1) and brown (Series8) lines in each of these plots, it appears that in the +30º orientation, all Series1 points are well above all Series8 plots, and in the -30º orientation the opposite is true – all Series8 points are well above all Series1 points. In the parallel case, all eight series points are crammed together between 140 & 160mm. The physical distance between the sensor and my ‘plane’ (shoebox) was measured at about 165mm, pretty close to the sensor values in the parallel case. So, it looks like it should be pretty easy to discern parallel, +30º, and -30º conditions, and probably reasonable to estimate the +/-10º and +/-20º cases as well.

18 January 2023 Update:

Today it occurred to me that I didn’t really know how the VL53L5CX sensor would respond to ‘wall’ angle changes when oriented in the ‘other’ direction (with the sensor oriented vertical to the floor instead of horizontally as it was above). So, I re-oriented the plugboard in my vise with the sensor mounted vertically, and redid the above experiments, with the results as shown below:

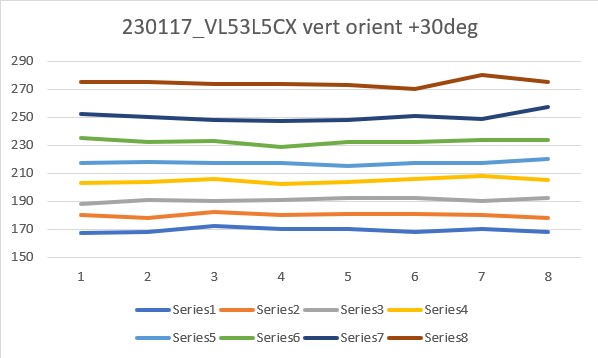
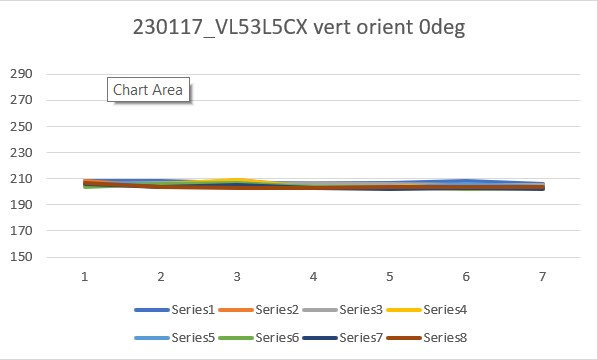
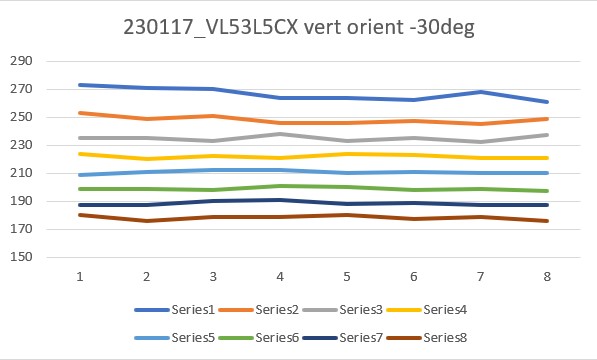
From the above results, it appears that the ‘sensor vertical’ case is more suited to plane orientation measurement than the ‘sensor horizontal’ one. Not sure why this is, but the data is pretty clear.

19 January 2023 Update:

In another email exchange with John Kvam, he wasn’t happy with the fact that the ‘sensor horizontal’ and ‘sensor vertical’ results were different, as the beam transmit/receive geometry is a square pyramid. He thinks some of the beam might be missing the top of the ‘wall’ or hitting the floor, distorting the results (presumably of the ‘horizontal sensor’ results, as the ‘vertical sensor’ results look pretty clean.

So, to address this question, I did another set of runs with the ‘resolution’ parameter set to “4×4” rather than the default “8×8”, and redid the experiments with both ‘horizontal’ and ‘vertical’ sensor orientation, with the following results:

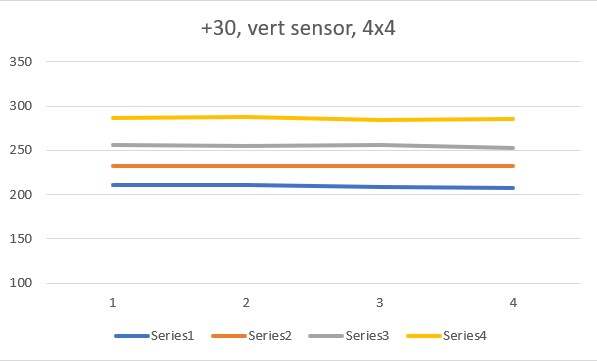
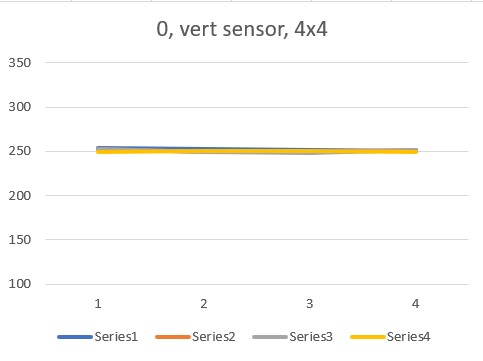
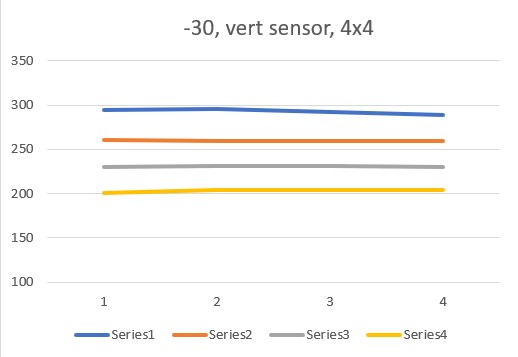
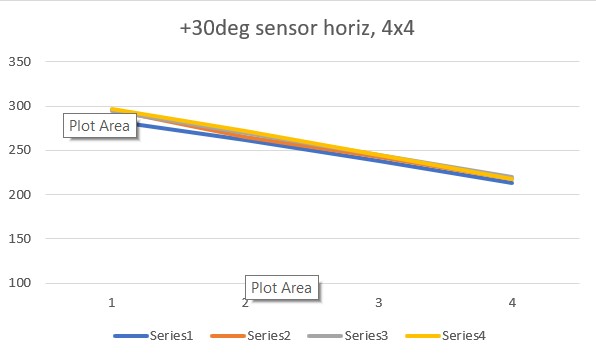
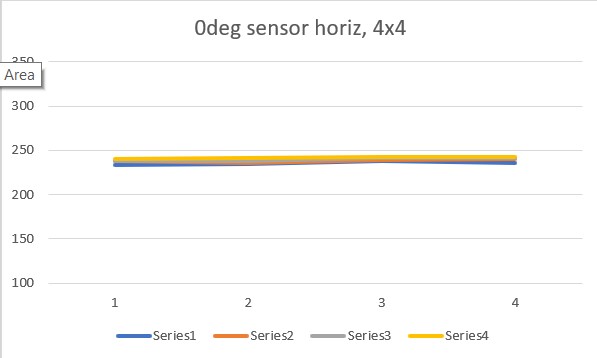
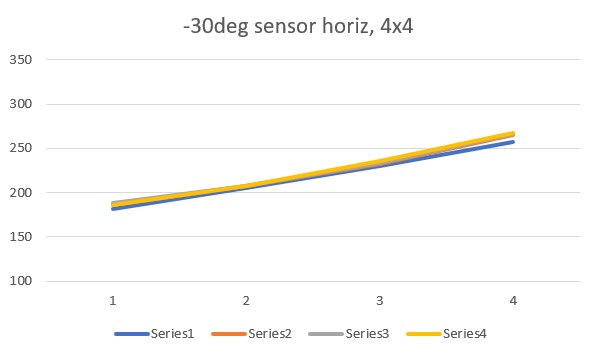
The ‘4×4’ plots above agree quite well with the original set of ‘8×8’ plots, in both shape and magnitude. However, they still show differences between the ‘horizontal’ and ‘vertical’ sensor orientations, which is not what John was expecting.

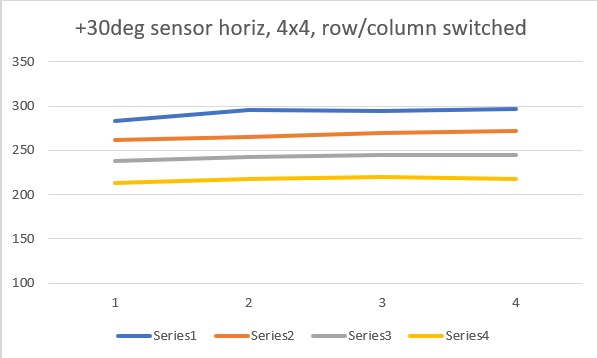
It occurred to me that the output from my little Sparkfun example is either a 4×4 or 8×8 array of sensor values, so I wasn’t sure what the ‘proper’ way of plotting this data was – I had just accepted Excel’s default which was to plot row by row. As an experiment, I tried switching the rows and columns, whereupon I got the following plots:

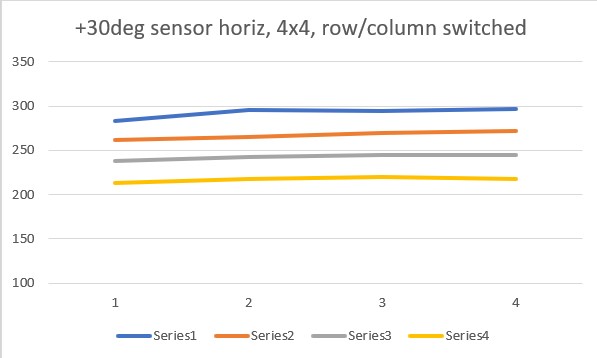
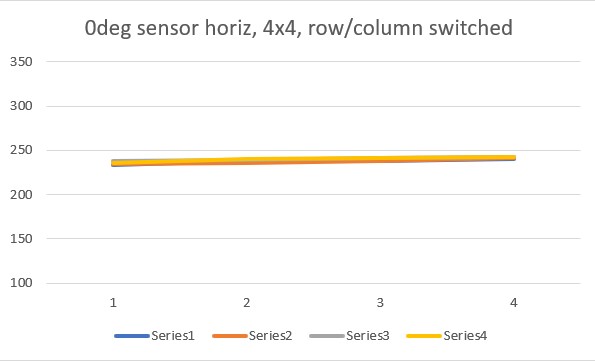
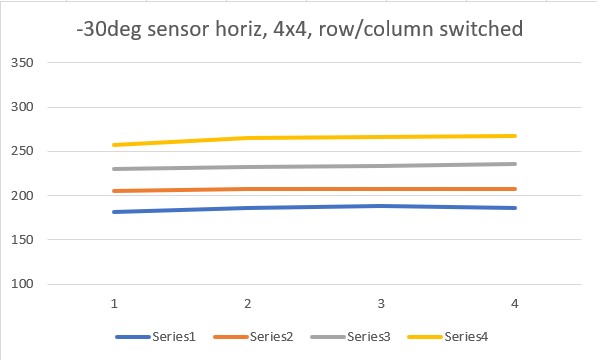
So it appears you can get the same result from both horizontal and vertical orientations, but you have to switch the row/column plotting order to get it. Another way to put it would be that you can select which plot behavior you want by selecting the row/column plotting order – interesting!

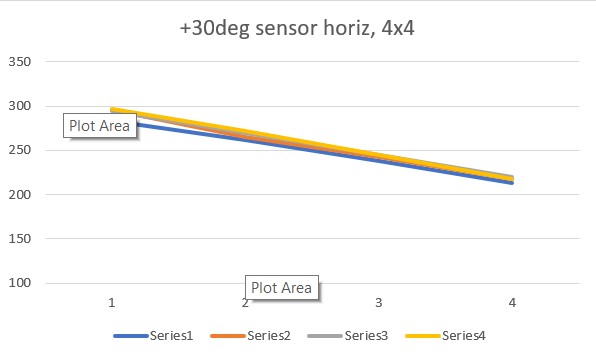
To recap this point, here’s a typical 4×4 output:

283	262	238	213
296	265	243	218
295	270	245	220
297	272	245	218

283 262 238 213

296 265 243 218

295 270 245 220

297 272 245 218

If this is plotted in normal row by row order, you get this plot:

But the same data, plotted in column by column order produces this plot:

Here’s the actual code that produces the output data:

#include <Wire.h>

#include <SparkFun_VL53L5CX_Library.h> //http://librarymanager/All#SparkFun_VL53L5CX

SparkFun_VL53L5CX myImager;
VL53L5CX_ResultsData measurementData; // Result data class structure, 1356 byes of RAM

int imageResolution = 0; //Used to pretty print output
int imageWidth = 0; //Used to pretty print output

void setup()
{
  Serial.begin(115200);
  delay(1000);
  Serial.println("SparkFun VL53L5CX Imager Example");

  Wire.begin(); //This resets to 100kHz I2C

  Serial.println("Initializing sensor board. This can take up to 10s. Please wait.");
  if (myImager.begin() == false)
  {
    Serial.println(F("Sensor not found - check your wiring. Freezing"));
    while (1);
  }

  //myImager.setResolution(8 * 8); //Enable all 64 pads
  myImager.setResolution(4 * 4); //01/18/23 rev to use 4x4 array

  imageResolution = myImager.getResolution(); //Query sensor for current resolution - either 4x4 or 8x8
  imageWidth = sqrt(imageResolution); //Calculate printing width

  myImager.startRanging();
}

void loop()
{
  //Poll sensor for new data
  if (myImager.isDataReady() == true)
  {
    if (myImager.getRangingData(&measurementData)) //Read distance data into array
    {
      //The ST library returns the data transposed from zone mapping shown in datasheet
      //Pretty-print data with increasing y, decreasing x to reflect reality
      for (int y = 0; y <= imageWidth * (imageWidth - 1); y += imageWidth)
      {
        for (int x = imageWidth - 1; x >= 0; x--)
        {
          Serial.print("\t");
          Serial.print(measurementData.distance_mm[x + y]);
        }
        Serial.println();
      }
      Serial.println();
    }
  }

  delay(5); //Small delay between polling
}

#include <Wire.h>

#include <SparkFun_VL53L5CX_Library.h> //http://librarymanager/All#SparkFun_VL53L5CX

SparkFun_VL53L5CX myImager;

VL53L5CX_ResultsData measurementData; // Result data class structure, 1356 byes of RAM

int imageResolution = 0; //Used to pretty print output

int imageWidth = 0; //Used to pretty print output

void setup()

{

Serial.begin(115200);

delay(1000);

Serial.println("SparkFun VL53L5CX Imager Example");

Wire.begin(); //This resets to 100kHz I2C

Serial.println("Initializing sensor board. This can take up to 10s. Please wait.");

if (myImager.begin() == false)

{

Serial.println(F("Sensor not found - check your wiring. Freezing"));

while (1);

}

//myImager.setResolution(8 * 8); //Enable all 64 pads

myImager.setResolution(4 * 4); //01/18/23 rev to use 4x4 array

imageResolution = myImager.getResolution(); //Query sensor for current resolution - either 4x4 or 8x8

imageWidth = sqrt(imageResolution); //Calculate printing width

myImager.startRanging();

}

void loop()

{

//Poll sensor for new data

if (myImager.isDataReady() == true)

{

if (myImager.getRangingData(&measurementData)) //Read distance data into array

{

//The ST library returns the data transposed from zone mapping shown in datasheet

//Pretty-print data with increasing y, decreasing x to reflect reality

for (int y = 0; y <= imageWidth * (imageWidth - 1); y += imageWidth)

{

for (int x = imageWidth - 1; x >= 0; x--)

{

Serial.print("\t");

Serial.print(measurementData.distance_mm[x + y]);

}

Serial.println();

}

Serial.println();

}

delay(5); //Small delay between polling

}

The line

    if (myImager.getRangingData(&measurementData)) //Read distance data into array

1	if (myImager.getRangingData(&measurementData)) //Read distance data into array

Reads the entire 4×4 or 8×8 array into memory, and then the doubly-indexed loop prints it out. This is all pretty straightforward, except for how the data is interpreted graphically. As the comments in the code indicate, the printout indexing arrangement is intended to flip the data to undo the physical transformation produced by the physical arrangement of sensor’s transmitter and receiver.

My use case, where all I want is the robot’s orientation angle w/r/t a nearby wall, I don’t really care if the data is transposed horizontally or vertically, as long as it stays the same from measurement to measurement. So, I’m beginning to think that I could simply select the array loading and/or plotting arrangement that gives me the ‘sloped line’ version, and derive the wall orientation from the slope of any of the 4 (or 8) lines

21 January 2023 Update:

After getting the SparkFun VL53L5CXA demo to work, I modified it to compare the first and last values from the first line of the 4×4 measurement array, and used the difference between these values to drive a small RC servo with an attached VL53L5CX module. Then I moved my ‘wall’ around to verify that the setup would, in fact, track the wall plane. Here’s the entire program:

/*
    Name:       VL53L5CX_ParallelFind_V1.ino
    Created:	1/20/2023 8:04:48 PM
    Author:     FRANKNEWXPS15\Frank

    Experiment to see if I can use a VL53L5CX to find the parallel orientation to a nearby wall
    Starts with the code from Sparkfun's VL53L5CX 'Example 1' demo program.

    Uses a VL53L5CX mounted horizontally on a servo motor.  The program seeks to equalize 
    sensor readings across a row.
*/


#include <Wire.h>

#include <SparkFun_VL53L5CX_Library.h> //http://librarymanager/All#SparkFun_VL53L5CX
#include <Servo.h>

Servo myservo;  // create servo object to control a servo
// twelve servo objects can be created on most boards

uint16_t servopos = 0;// variable to store the servo position

SparkFun_VL53L5CX myImager;
VL53L5CX_ResultsData measurementData; // Result data class structure, 1356 byes of RAM

int imageResolution = 0; //Used to pretty print output
int imageWidth = 0; //Used to pretty print output
bool bAutoMode = true;//used to break out of manual positioning
int16_t curServoPos = 0;
int16_t newServoPos = 0;

void setup()
{
  Serial.begin(115200);//baud rate ignored by Teensy
  delay(1000);
  Serial.println("SparkFun VL53L5CX Imager Example");

  Wire.begin(); //This resets to 100kHz I2C

  Serial.printf("%lu: Initializing sensor board. This can take up to 10s. Please wait\n", millis());
  if (myImager.begin() == false)
  {
    Serial.println(F("Sensor not found - check your wiring. Freezing"));
    while (1);
  }

  Serial.printf("%lu: Sensor ready!\n", millis());

  //myImager.setResolution(8 * 8); //Enable all 64 pads
  myImager.setResolution(4 * 4); //01/18/23 rev to use 4x4 array

  imageResolution = myImager.getResolution(); //Query sensor for current resolution - either 4x4 or 8x8
  imageWidth = sqrt(imageResolution); //Calculate printing width

  myImager.startRanging();
  myservo.attach(9);  // attaches the servo on pin 9 to the servo object
  //myservo.write(servopos); // tell servo to go to position 0

  delay(15); // waits 15ms for the servo to reach the position
}

void loop()
{
  CheckForUserInput();

  //Poll sensor for new data
  if (myImager.isDataReady() == true)
  {
    if (myImager.getRangingData(&measurementData)) //Read distance data into array
    {
      //The ST library returns the data transposed from zone mapping shown in datasheet
      //Pretty-print data with increasing y, decreasing x to reflect reality
      for (int y = 0; y <= imageWidth * (imageWidth - 1); y += imageWidth)
      {
        for (int x = imageWidth - 1; x >= 0; x--)
        {
          Serial.print("\t");
          Serial.print(measurementData.distance_mm[x + y]);
        }
        Serial.println();
      }
      Serial.println();
    }
  }

  //now determine which way to move the servo to 'flatten' the line
  for (int x = imageWidth - 1; x >= 0; x--)
  {
    Serial.print("\t");
    Serial.print(measurementData.distance_mm[x]);
  }

  Serial.print("\n");


  //if( D[imageWidth - 1 + y=0] > D[0 + y=0] then must be '+' angle; rotate CCW
  //else rotate CW

  int16_t delta = measurementData.distance_mm[imageWidth - 1] - measurementData.distance_mm[0];
  Serial.printf("first = %d, last = %d, delta = %d\n",
    measurementData.distance_mm[imageWidth - 1], 
    measurementData.distance_mm[0], 
    delta);

  if (delta > 0)
  {
    newServoPos -= 10;
  }
  else if (delta < 0)
  {
    newServoPos += 10;
  }
  //if delta == 0, no change

  Serial.printf("current pos = %d, delta = %d, new pos = %d\n",curServoPos, delta, newServoPos);

  Serial.printf("Writing %d to servo\n", newServoPos);
  myservo.write(newServoPos);

  curServoPos = newServoPos;

  delay(500); //Small delay between polling
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

Name: VL53L5CX_ParallelFind_V1.ino

Created: 1/20/2023 8:04:48 PM

Author: FRANKNEWXPS15\Frank

Experiment to see if I can use a VL53L5CX to find the parallel orientation to a nearby wall

Starts with the code from Sparkfun's VL53L5CX 'Example 1' demo program.

Uses a VL53L5CX mounted horizontally on a servo motor. The program seeks to equalize

sensor readings across a row.

#include <Wire.h>

#include <SparkFun_VL53L5CX_Library.h> //http://librarymanager/All#SparkFun_VL53L5CX

#include <Servo.h>

Servo myservo; // create servo object to control a servo

// twelve servo objects can be created on most boards

uint16_t servopos = 0;// variable to store the servo position

SparkFun_VL53L5CX myImager;

VL53L5CX_ResultsData measurementData; // Result data class structure, 1356 byes of RAM

int imageResolution = 0; //Used to pretty print output

int imageWidth = 0; //Used to pretty print output

bool bAutoMode = true;//used to break out of manual positioning

int16_t curServoPos = 0;

int16_t newServoPos = 0;

void setup()

{

Serial.begin(115200);//baud rate ignored by Teensy

delay(1000);

Serial.println("SparkFun VL53L5CX Imager Example");

Wire.begin(); //This resets to 100kHz I2C

Serial.printf("%lu: Initializing sensor board. This can take up to 10s. Please wait\n", millis());

if (myImager.begin() == false)

{

Serial.println(F("Sensor not found - check your wiring. Freezing"));

while (1);

}

Serial.printf("%lu: Sensor ready!\n", millis());

//myImager.setResolution(8 * 8); //Enable all 64 pads

myImager.setResolution(4 * 4); //01/18/23 rev to use 4x4 array

imageResolution = myImager.getResolution(); //Query sensor for current resolution - either 4x4 or 8x8

imageWidth = sqrt(imageResolution); //Calculate printing width

myImager.startRanging();

myservo.attach(9); // attaches the servo on pin 9 to the servo object

//myservo.write(servopos); // tell servo to go to position 0

delay(15); // waits 15ms for the servo to reach the position

}

void loop()

{

CheckForUserInput();

//Poll sensor for new data

if (myImager.isDataReady() == true)

{

if (myImager.getRangingData(&measurementData)) //Read distance data into array

{

//The ST library returns the data transposed from zone mapping shown in datasheet

//Pretty-print data with increasing y, decreasing x to reflect reality

for (int y = 0; y <= imageWidth * (imageWidth - 1); y += imageWidth)

{

for (int x = imageWidth - 1; x >= 0; x--)

{

Serial.print("\t");

Serial.print(measurementData.distance_mm[x + y]);

}

Serial.println();

}

Serial.println();

}

//now determine which way to move the servo to 'flatten' the line

for (int x = imageWidth - 1; x >= 0; x--)

{

Serial.print("\t");

Serial.print(measurementData.distance_mm[x]);

}

Serial.print("\n");

//if( D[imageWidth - 1 + y=0] > D[0 + y=0] then must be '+' angle; rotate CCW

//else rotate CW

int16_t delta = measurementData.distance_mm[imageWidth - 1] - measurementData.distance_mm[0];

Serial.printf("first = %d, last = %d, delta = %d\n",

measurementData.distance_mm[imageWidth - 1],

measurementData.distance_mm[0],

delta);

if (delta > 0)

{

newServoPos -= 10;

}

else if (delta < 0)

{

newServoPos += 10;

}

//if delta == 0, no change

Serial.printf("current pos = %d, delta = %d, new pos = %d\n",curServoPos, delta, newServoPos);

Serial.printf("Writing %d to servo\n", newServoPos);

myservo.write(newServoPos);

curServoPos = newServoPos;

delay(500); //Small delay between polling

}

And here is a short video showing the results:

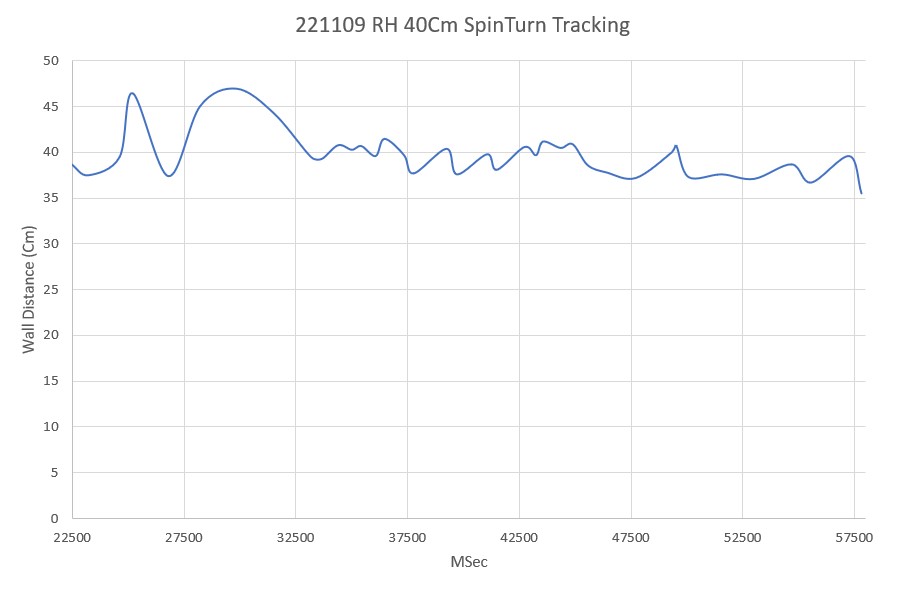
In the above, the servo is moved in 10deg steps to attempt to zero out the difference between the first and last distance measurements from the first row of the 4×4 array. The loop timing (500mSec/loop) is very slow and the algorithm is a simple as it gets, but it appears that this very simple algorithm actually works pretty well.

Next steps are to reduce the loop delay, and reduce the servo step size from 10deg to 1deg, or even use a step size proportional to the error term. Here’s another short video showing the tracking behavior with a 30Hz ranging frequency and a slightly more aggressive servo positioning algorithm.

So it appears clear that the VL53L5CX can be used to track a nearby wall, at least in this servo-enabled configuration. The remaining question is, can I substitute my robot’s wheel motors in the place of the above RC servo and get the same sort of ‘parallel tracking’ behavior as shown above. If not, then I might still be able to use a single sensor per side by mounting it on a servo as in the above configuration. The servo-mounted configuration might even be better, as the sensor would remain broadside to the nearby wall, even if the robot wasn’t. This might facilitate better ‘move to desired left/right distance’ performance because no distance compensation for orientation would be required, and better wall offset tracking for the same reason.

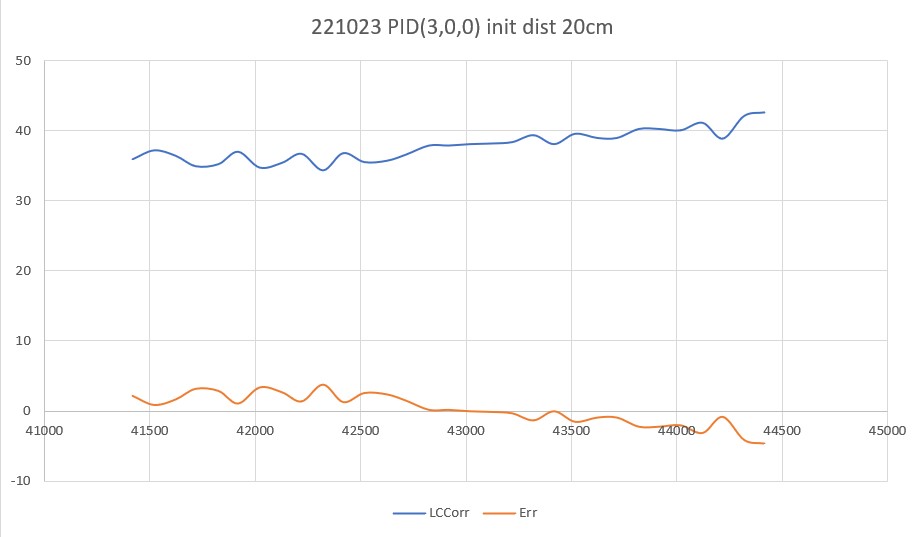
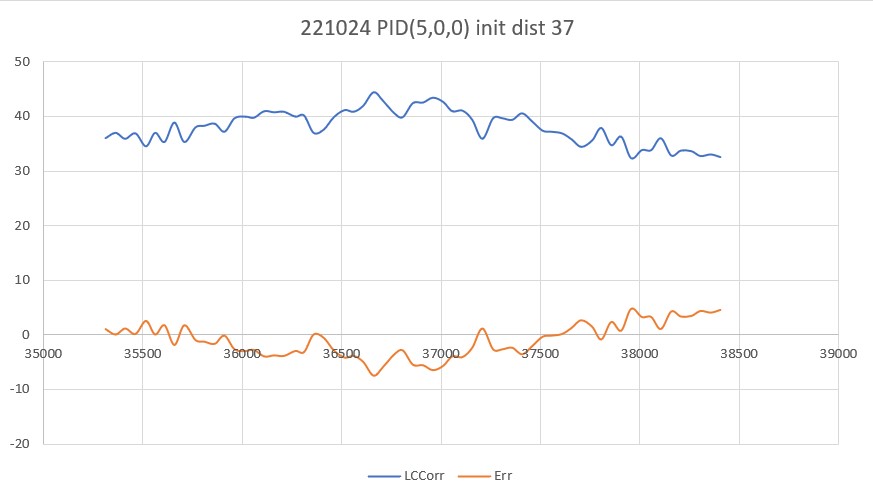
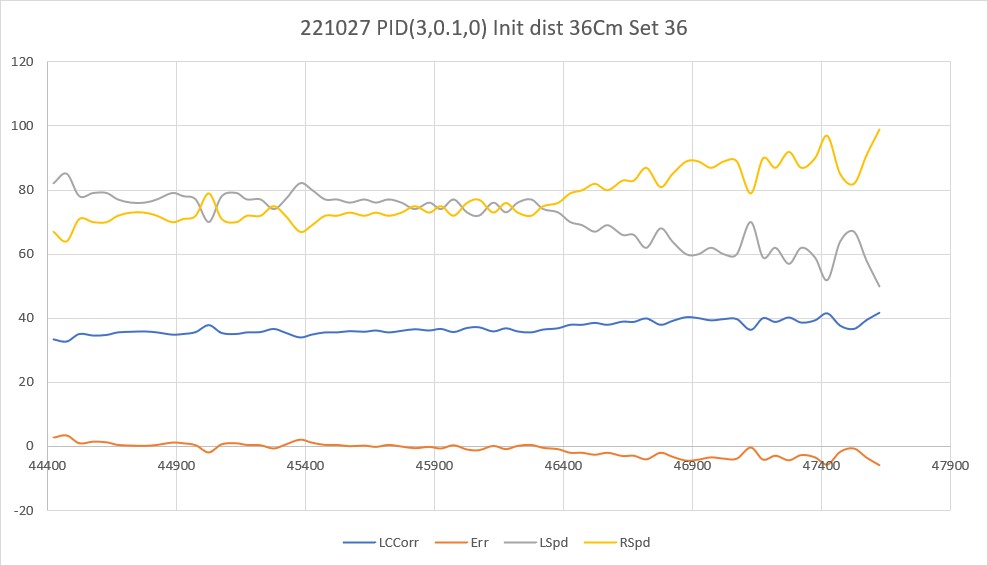
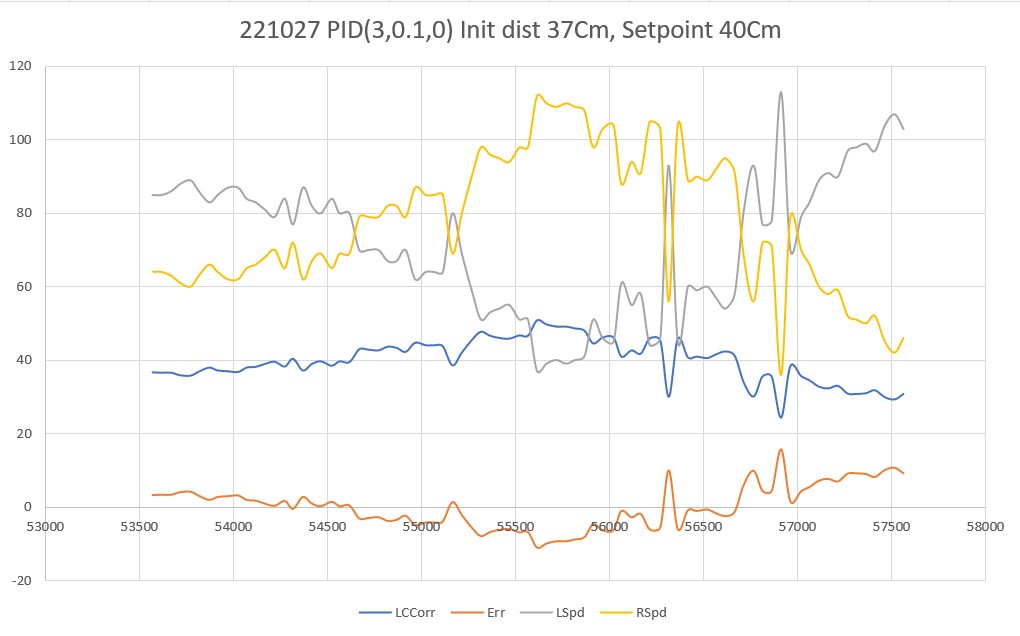
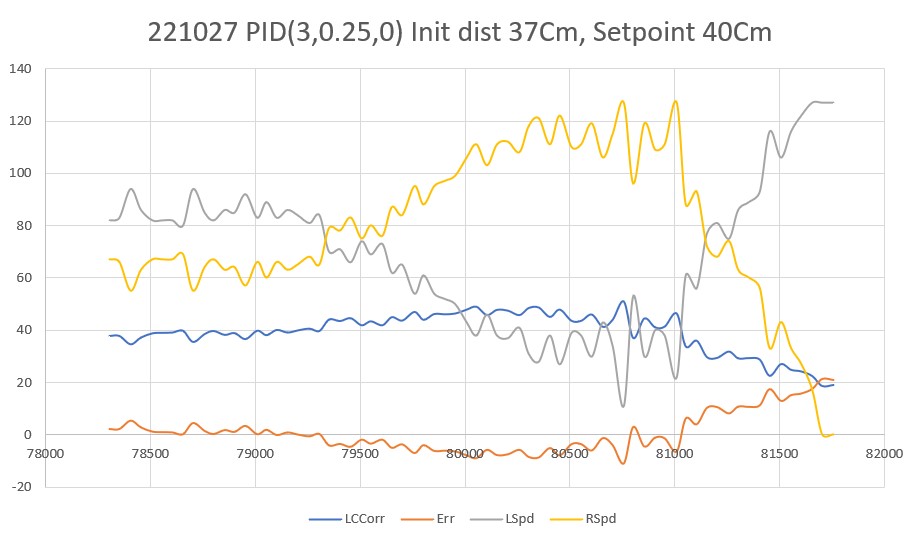
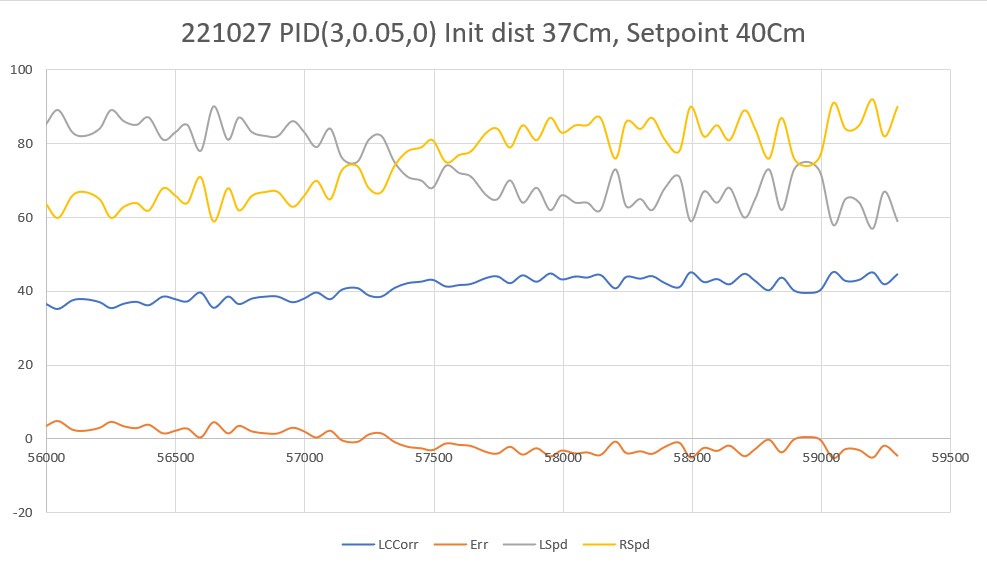
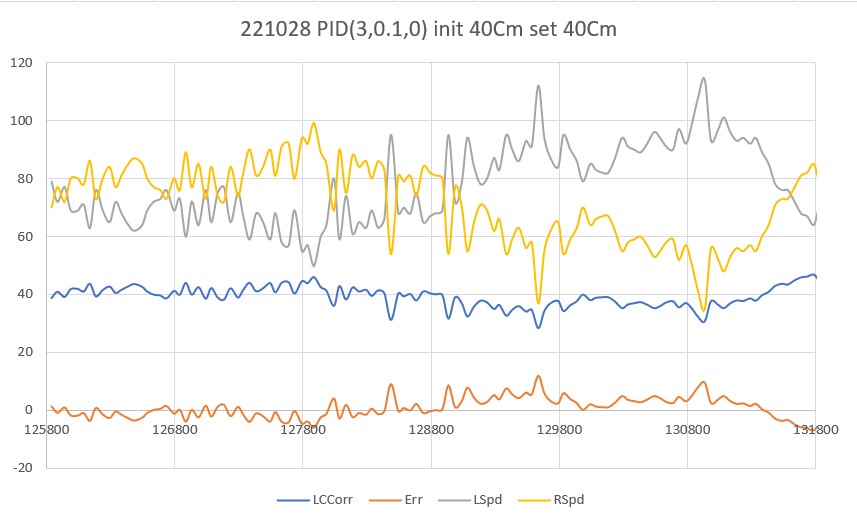
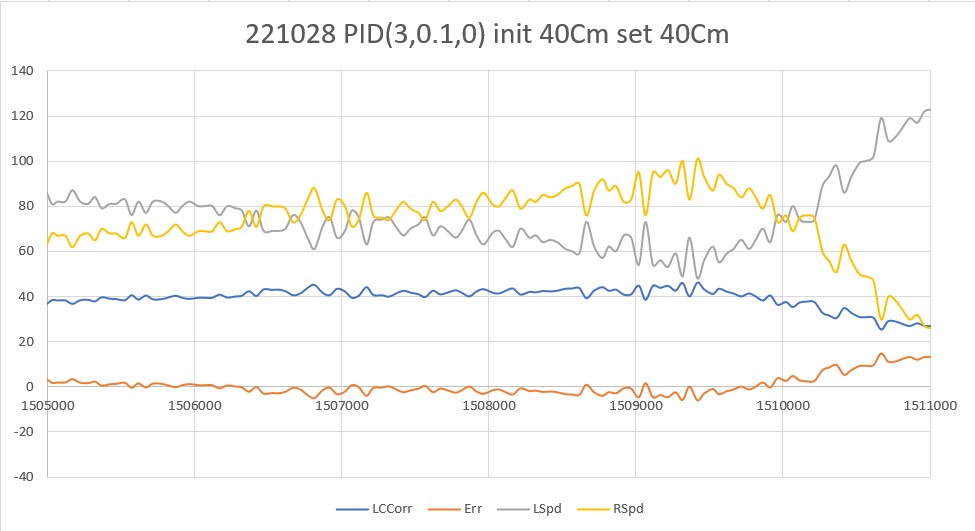
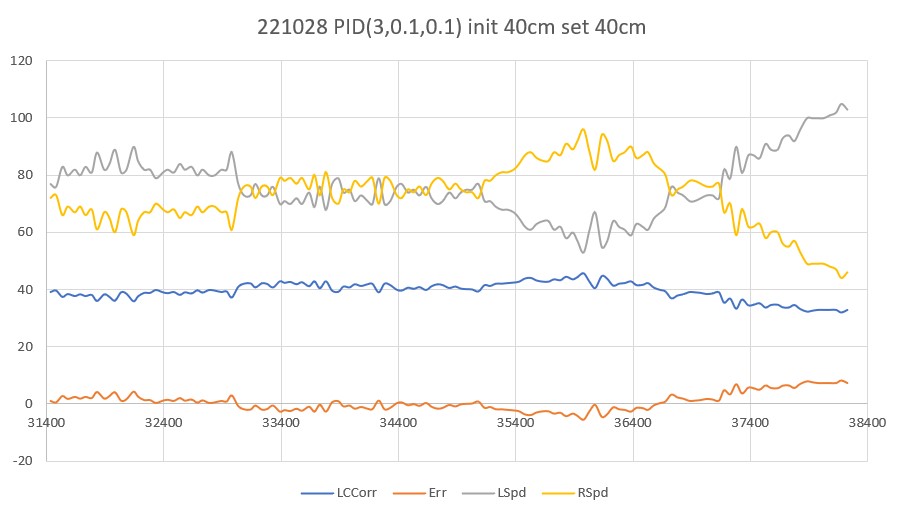
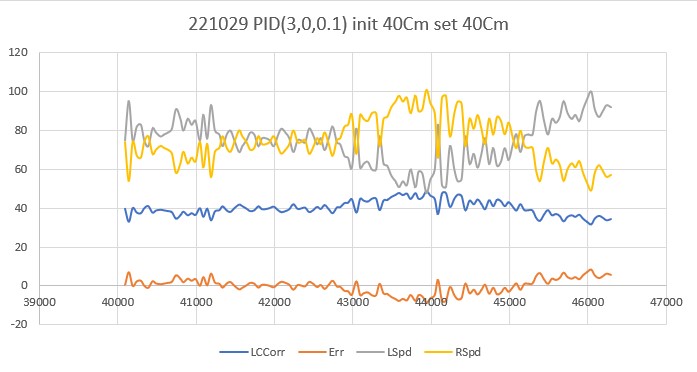
20 March 2023 Update:

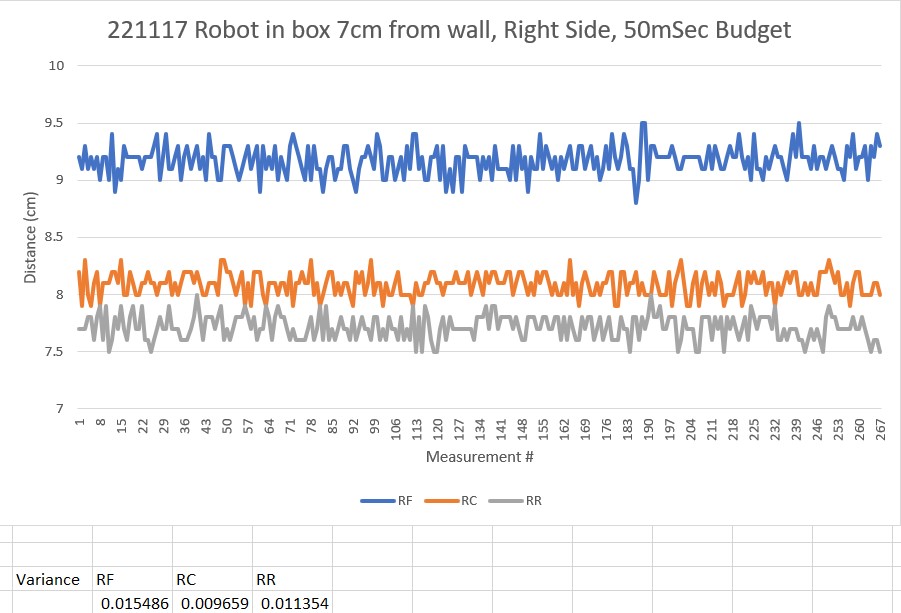
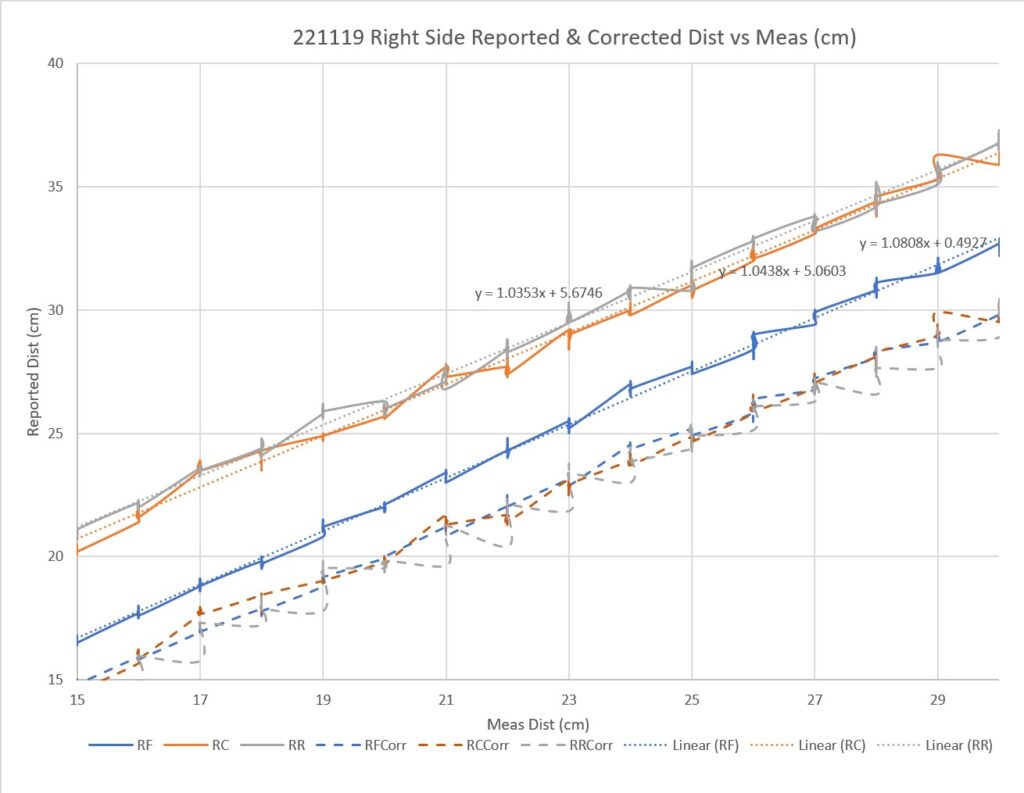
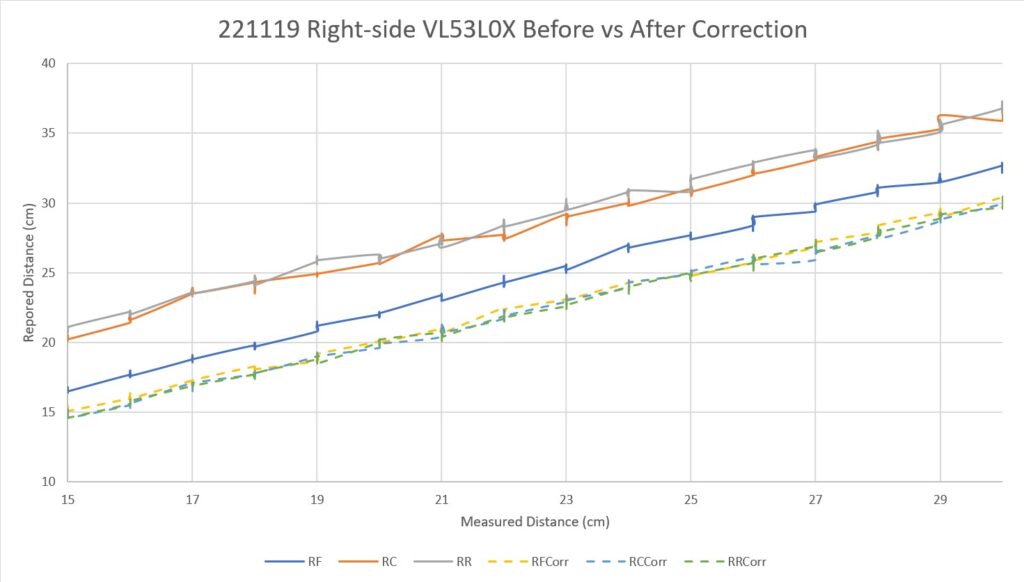
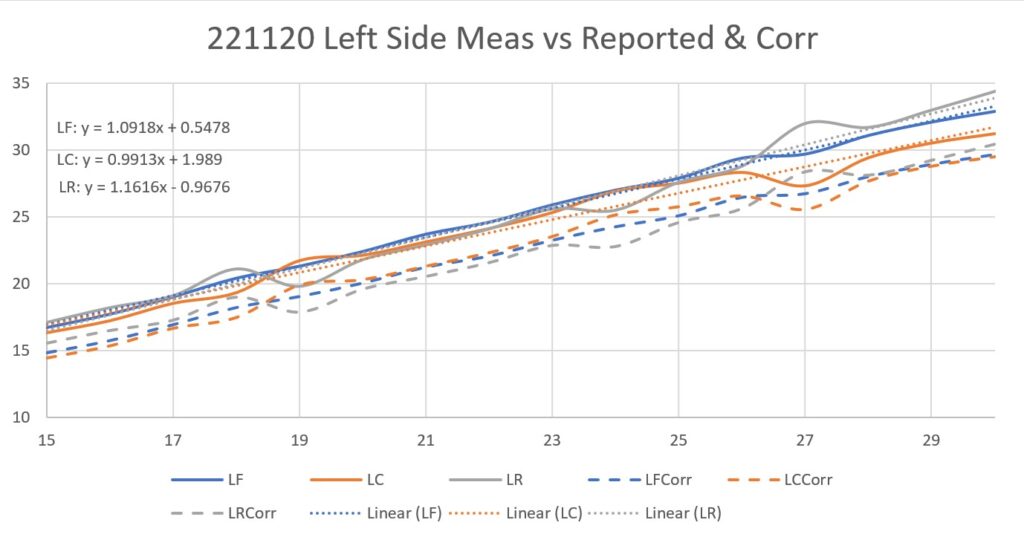
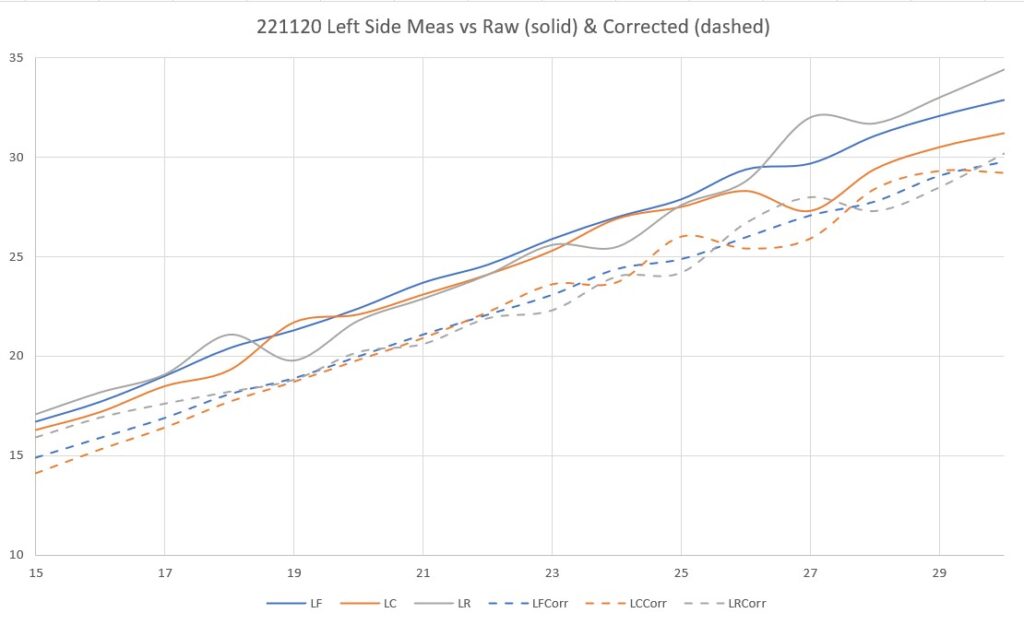
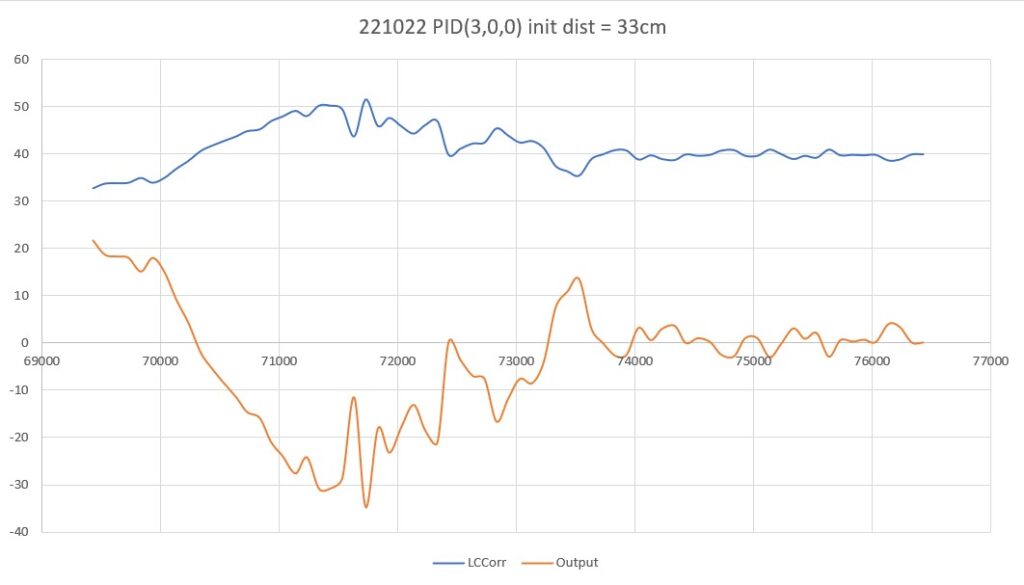
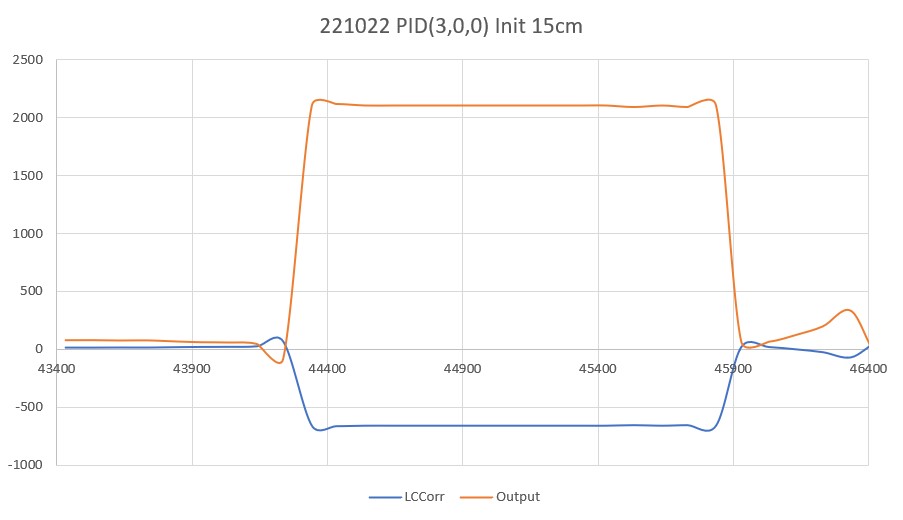
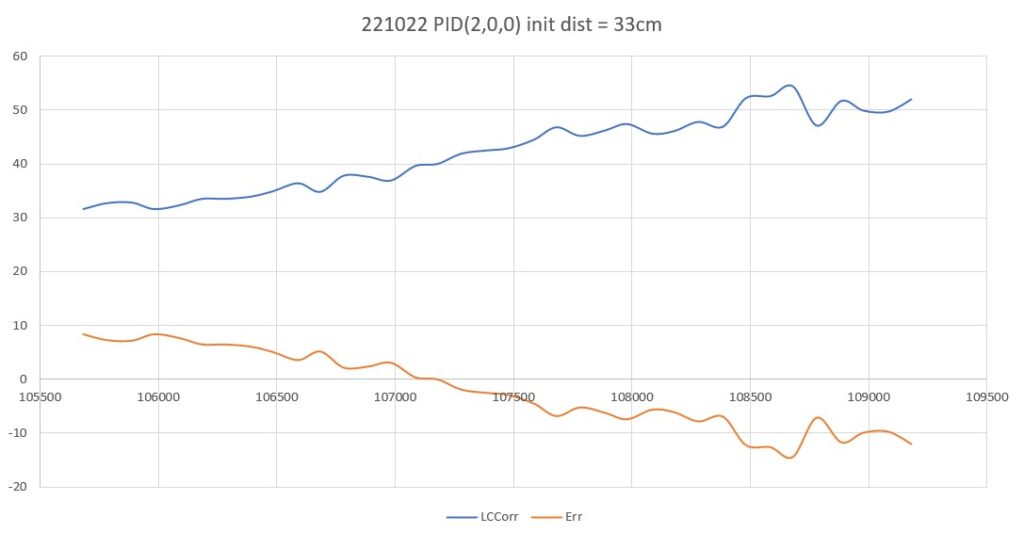
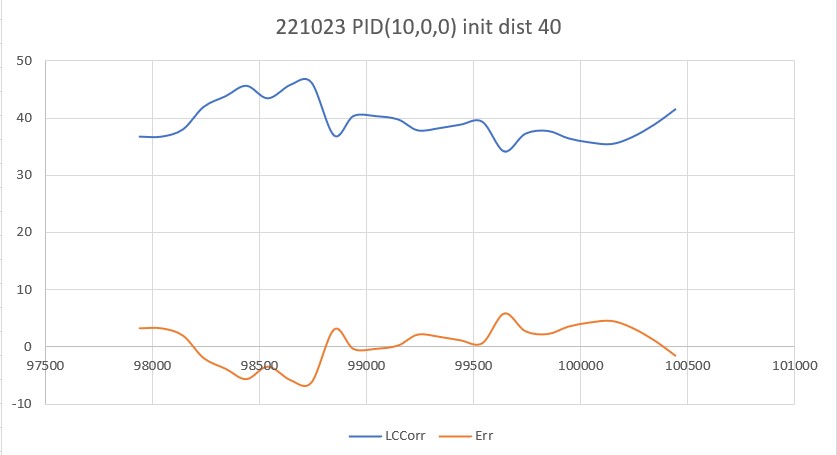
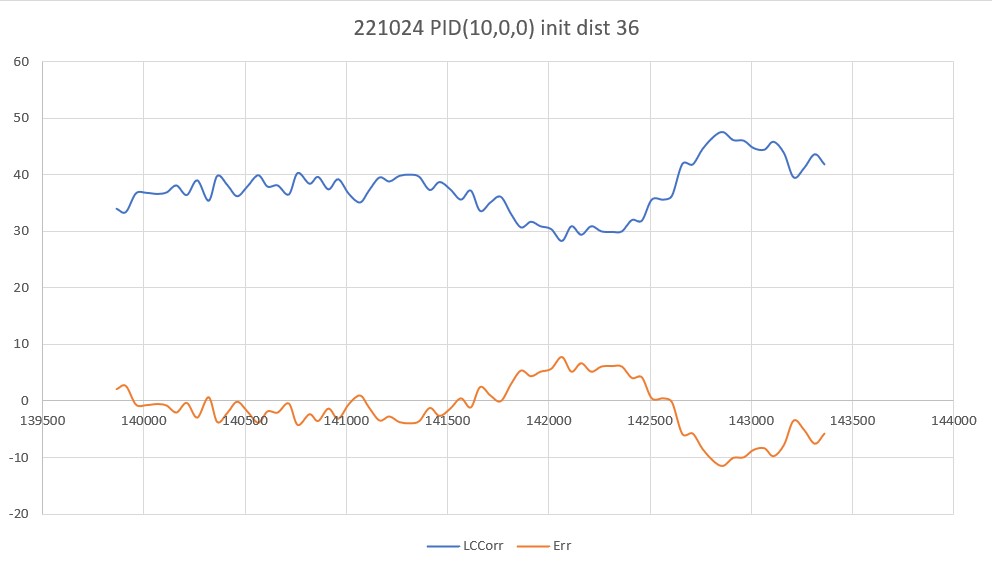
As one result of my recent ‘field’ tests with ‘WallE3_Complete_V2’ (see this post), I discovered that the maximum distance capability (approximately 120cm) of my VL53L0X sensors was marginal for some of the tracking cases. In particular, when the robot passes an open doorway on the tracking side, it attempts to switch to the ‘other’ wall, if it can find one. However, If the robot is tracking the near wall at a 40cm offset, and the other wall is more than 120cm further away (160cm total), then the robot may or may not ‘see’ the other wall during an ‘open doorway’ event. I could probably address this issue by setting the tracking offset to 50cm vs 40cm, but even that might still be marginal. This problem is exacerbated by any robot orientation changes while tracking, as even a few degrees of ‘off-perpendicular’ orientation could cause the distance to the other wall to fall outside the sensor range – bummer.

The real solution to the above problem is to get a better side-distance sensor, just as I did by changing from the Pulsed Light LIDAR front distance sensor to the Garmin LIDAR-Lite V4/LED one. For the VL53L0X side sensor, the logical choice is the VL53L5CX sensor; not only does the -5CX sensor have more range (200-400cm), but as I was able to demonstrate above, only one sensor per side is required for orientation sensing. The downside is it will require quite a bit of reconfiguration of the second deck, both in terms of hardware and software – ugh!

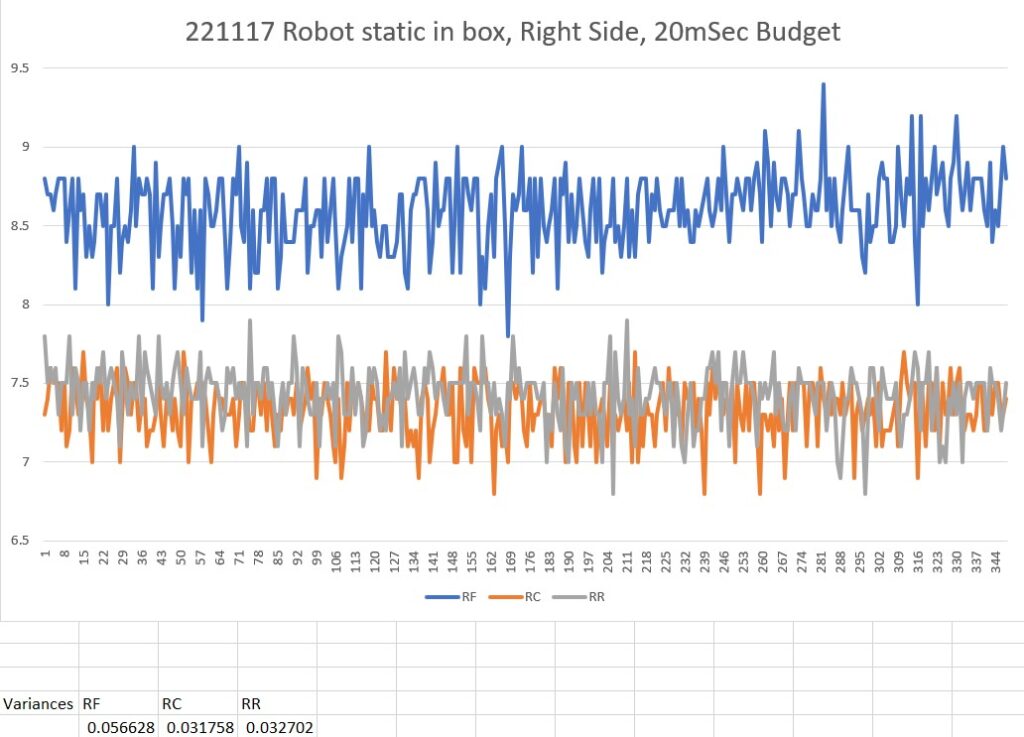
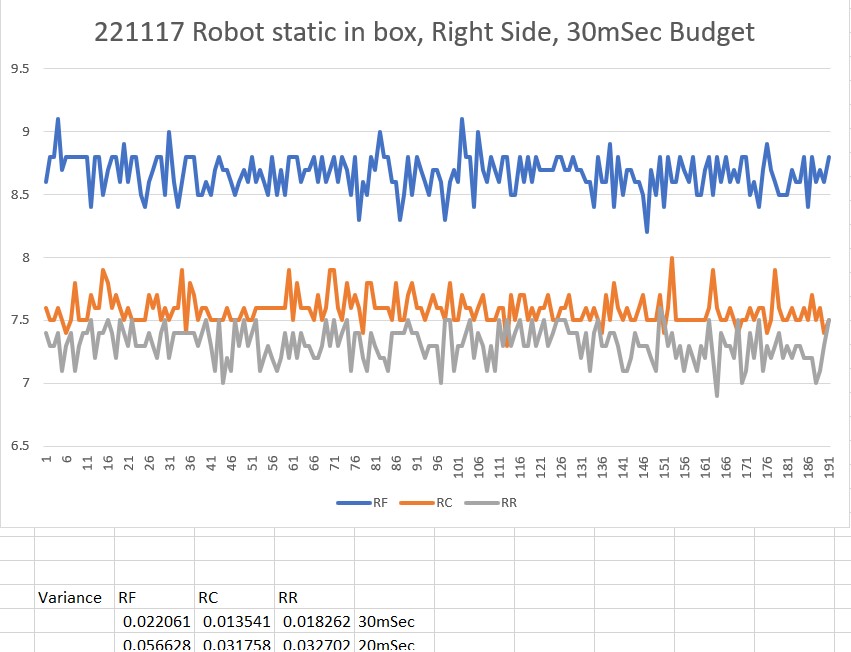
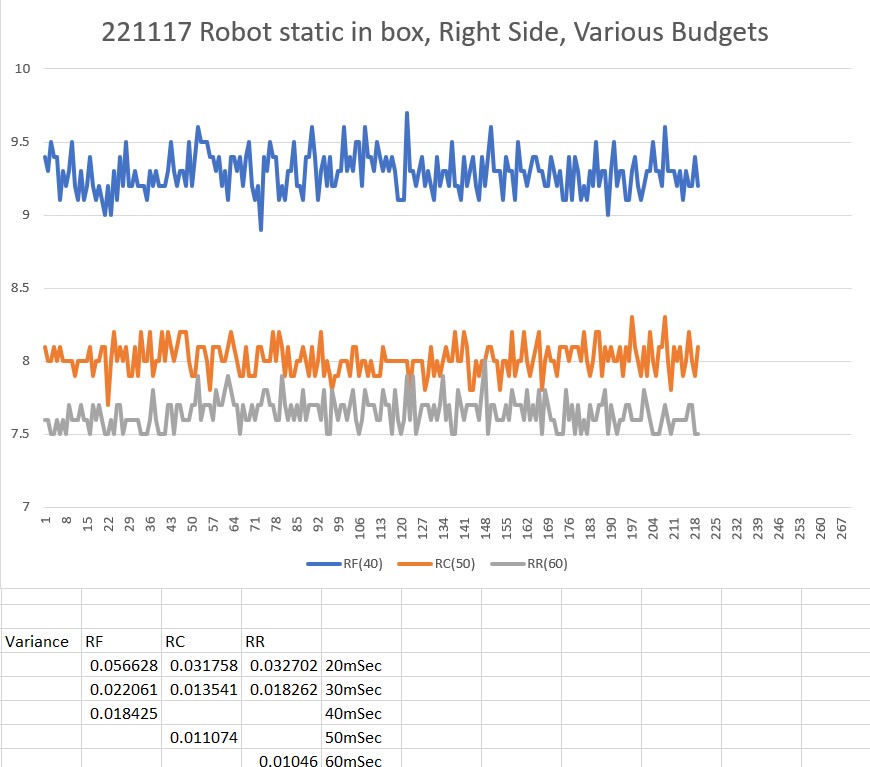
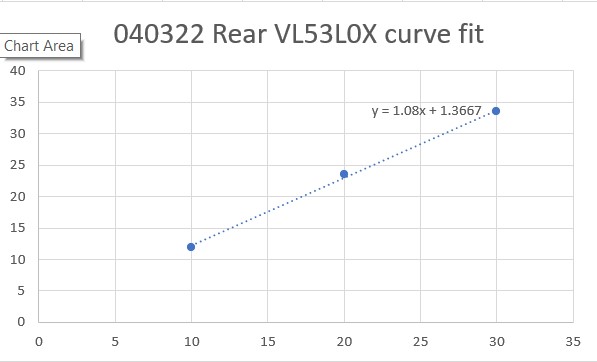
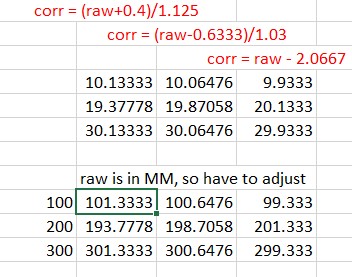
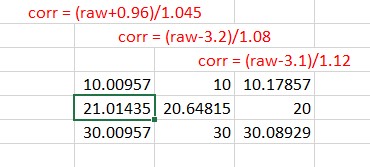
To confirm the distance specs for the VL53L5CX sensor, I reconstructed the above circuit from my and made some tests to measure the maximum distance, as shown below:

Unfortunately, the tests showed that I wasn’t really going to get any additional range out of the VL53L5CX unit, and in addition range determination would be complicated by the fact that the field-of-view for the VL53L5CX is much broader than for the VL53L0X. This would mean that when mounted on WallE3’s second deck, the sensor would ‘see’ the floor as well as the target wall, giving skewed readings across the array. I think I would still be able to figure that out (i.e. only look at the SPADS on the bottom or top, whichever corresponds to ‘not floor’) but still a PITA. The big problem though, is that I no longer think the -5CX would be enough better to justify the expense (time and money and aggravation) of changing from the -0X. Bummer!

More to follow, stay tuned

Frank

Improving VL53L0X Measurement Accuracy/Precision

2 Replies

Posted 15 November 2022

Last April I described how I determined that individual VL53L0X ‘time-of-flight’ distances sensors exhibited measurement errors, and also described my method for minimizing those errors. This has worked well up to now, but I recently realized that there was another error term I hadn’t accounted for; the error associated with using integer variables to hold VL53L0X distance measurements.

The left & right 3-element VL53L0X arrays (plus a single rear distance sensor) are managed by a dedicated Teensy 3.5 processor, which retrieves distance measurements from all seven sensors and then calibrates them using the method described in my April post. When requested by the main processor, these measurements (in integer MM) are provided via a I2C link. After receipt from the VL53L0X processor, distance measurements are converted from MM to CM by dividing by 10, ignoring integer truncation.

However, I have recently discovered that this integer truncation may well be more significant that I originally thought, and may be leading to performance issues, particularly with my ‘RotateToParallelOrientation()’ function and wall offset tracking in general. The linear distance between the front and rear VL53L0X sensor on each side is about 8.5Cm. Assuming that all constant errors are calibrated out, the robot will be parallel to the wall when the front and rear sensors return the same value. However, because the distance values only change in 1Cm increments, the actual distances measured by the front and rear sensors can be as much as 1Cm different. 1Cm difference over a length of 8.5Cm is about 7∘ – small, but not necessarily insignificant.

It turned out to be relatively painless to change all VL53L0X distance variables from ‘uint16_t’ to ‘float’, and get everything going again. After making this change I tried some more ‘rotate to parallel’ experiments but the change didn’t seem to make much of an improvement. Poking around a bit more I found out why – the raw measurement data coming from the VL53L0X sensors exhibited a lot of ‘noise’, even with the robot stationary and only a few cm from the nearby ‘wall’. The following Excel plot shows one sensor’s data with the robot approximately 14cm from the wall.

As can be seen from the above the reported distance varies from 13 to about 14.5cm. Assuming that all three right-hand sensors behave similarly, it would be possible for the front sensor to report 13cm while the rear sensor was reporting 14.5cm. Moreover, my parallel find algorithm defines ‘parallel’ as RF-RR ~= 0, so it can (and does) terminate well before or after the actual physical parallel orientation occurs.

Looking through (again) the VL53L0X documentation, I came across the ‘measurement budget’ parameter, which is set by default to ‘30000’ (30msec). In my application I had it set to ‘20000’ (20msec) because I thought at the time that with 7 total VL53L0X sensors, I couldn’t afford 30msec delay for each and still hold to a 200msec system loop period. I later changed the system design to use a separate Teensy 3.5 to continuously poll the sensors and report the latest measurement to the main processor when asked, which essentially eliminated the sensor delay from the overall loop (not entirely, as longer sensor measurement times may mean that physical dynamics aren’t followed quite as faithfully, but fortunately my robot doesn’t do anything quickly).

To test the effect of longer measurement budgets, I placed my robot in a cardboard box with its right-side sensor array about 7cm from the wall of the box, and then took measurements with measurement budgets of20, 30, 40, 50, and 60msec. For each value I plotted the distance output and also calculated the variance for each sensor, as shown in the plots below:

20msec budget – the current configuration

30mse budge with 20 & 30msec variances shown

Showing the effect of 40, 50 & 60 msec budgets

As can be seen from the chart immediately above, a measurement budget of 50msec is noticeably better than that for 40msec (which is itself better than the 20 or 30msec budgets), but the 60msec budget plot shows little improvement over 50msec. Looking The ‘RF’ variance starts at 0.0566 for 20msec, drops to less than half that at 30msec, drops by half again at 40msec, and drops by another 50% or so at 50msec. From there to 60msec is only a change from 0.011074 to 0.01046 (this all assumes that I can draw conclusions like this when not only going up with measurement budget, but going across sensors as well). In any case, I settled on a new measurement budge value of 50msec, as shown below.

New value of 50msec for measurement budget

Note that while the motionless measurement variation has been significantly improved, I still have a problem with different nominal measurements from each sensor; the right-front (RF) sensor insists the wall is about 9.2cm away, while the center (RC) and rear (RR) ones think the wall is about 8 and 7.7cm away, respectively (as a side note, before I changed reported measurement variables from ‘uint_16’ to ‘float’, these values would have been reported as 9,8, and 7cm respectively). I thought I had fixed this problem earlier with a set of correction functions as described here, but I obviously have some more work to do (see this post for more on distance correction)

Stay tuned,

Frank

VL53L0X Distance Measurement Compensation

4 Replies

Posted 20 November 2022

To study the issue of VL53L0X sensor calibration, I set up an experiment where ten measurements from each of the three right-side sensors were collected at distances from 15 – 30cm, as shown below. As can be seen, the ‘raw’ values (no correction) are pretty linear. I used Excel’s ‘trendline’ tool to display the ‘best fit’ linear expression for each line, then used these expressions to calculate a correction expression, (dashed lines)

The actual correction expressions were (cm units):

RF: RFCorr = (RF-0.4297)/1.0808
RC: RCCorr = (RC-5.0603)/1.0438
RR: RRCorr = =(RR-5.6746)/1.0353

Next, I edited my ‘lidar_XX_Correction()’ subroutines in my Teensy_7VL53L0X_I2C_Slave_V4 project to implement the above expressions, and made another run of distances from 15 to 30cm, as shown below.

Before (solid lines) and After (dashed lines) Correction

The above plot shows that the correction algorithm is effective and repeatable, at least on the right side sensors. Now I have to perform the same corrections on the left side and I’ll be all set – at least for this particular part of the ongoing Sisyphean task of educating WallE3, my somewhat retarded autonomous wall-following robot.

Applying the same methodology to the left side sensors, I first captured left-side reported distances for measured values from 15 to 30 cm, same as for the left side. Then, using Excel’s ‘trendline’ calculation feature to derive a correction expression, I added simulated correction lines to the plot, as shown below:

The actual correction expressions were (cm units):

LF: LFCorr = (LF – 0.5478)/1.0918
LC: LCCorr = (LC – 1.989)/0.9913)
LR: LRCorr = (LR + 0.9676)/1.1616

Not much correction is needed for the left-side sensors. However, since I already have the corrections, I might as well put them in; I modified the VL53L0X sensor manager firmware to include the above corrections, and then re-did the calibration plot -this time plotting the pre-correction reported data along with the post-correction reported data, as shown below:

As can be seen from the above plot, left-side correction is pretty good over the entire 15-30cm range – nice!

Stay tuned,

Frank

More Wall Track PID Tuning Work

1 Reply

Posted 15 October 2022

While working on my new ‘RunToDaylight’ algorithm for WallE3, my autonomous wall-following robot, I noticed that when WallE3 finds a wall to track after travelling in the direction of most front distance, it doesn’t do a very good job at all, oscillating crazily back and forth, and sometimes running head-first into the wall it is supposedly trying to track. This is somewhat disconcerting, as I thought I had long ago established a good wall tracking algorithm. So, I decided to once again plunge headlong into the swamps and jungles of my wall-tracking algorithm, hoping against hope that I won’t get eaten by mosquitos, snakes or crocodiles.

I went back to my latest part-task program, ‘WallE3_WallTrackTuning’. This program actually does OK when the robot starts out close to the wall, as the ‘CaptureWallOffset()’ routine is pretty effective. However, I noticed that when the robot starts out within +/- 4cm from the defined offset value, it isn’t terribly robust; the robot typically just goes straight with very few adjustments, even as it gets farther and farther away from the offset distance – oops!

So, I created yet another part-task program ‘WallE3_WallTrackTuning_V2’ to see if I could figure out why it isn’t working so well. With ‘WallE3_WallTrackTuning’ I simply called either TrackLeftWallOffset() or TrackRightWallOffset() and fed it the user-entered offset and PID values. However, this time I decided to pare down the code to the absolute minimum required to track a wall, as shown below (user input code not shown for clarity):

  while (true)
  {
    //10/16/22 starting over with wall track tuning
    float kp = WallTrack_Kp;
    float ki = WallTrack_Ki;
    float kd = WallTrack_Kd;

    float lastError = 0;
    float lastInput = 0;
    float lastIval = 0;
    float lastDerror = 0;
    WallTrackSetPoint = OffCm; //04/17/22 this value holds robot parallel to left wall

    gl_pSerPort->printf("\nTrackLeftWallOffset: Start tracking offset of %2.1fcm with Kp/Ki/Kd = %2.2f\t%2.2f\t%2.2f\n",
      WallTrackSetPoint, kp, ki, kd);

    gl_pSerPort->printf(WallFollowTelemHdrStr);

    //Step4: Track the wall using PID algorithm
    mSecSinceLastWallTrackUpdate = 0; //added 09/04/21
    MsecSinceLastFrontDistUpdate = 0; //added 10/02/22 to slow front LIDAR update rate

    while (true)
    {
      CheckForUserInput(); //this is a bit recursive, but should still work (I hope)

      if (mSecSinceLastWallTrackUpdate > WALL_TRACK_UPDATE_INTERVAL_MSEC)
      {
        mSecSinceLastWallTrackUpdate -= WALL_TRACK_UPDATE_INTERVAL_MSEC;

        //03/08/22 abstracted these calls to UpdateAllEnvironmentParameters()
        UpdateAllEnvironmentParameters();//03/08/22 added to consolidate sensor update calls

        //from Teensy_7VL53L0X_I2C_Slave_V3.ino: LeftSteeringVal = (LF_Dist_mm - LR_Dist_mm) / 100.f; //rev 06/21/20 see PPalace post
        float orientdeg = GetWallOrientDeg(glLeftSteeringVal);
        float orientrad = (PI / 180.f) * orientdeg; 
        float orientcos = cosf(orientrad);
        glLeftCentCorrCm = glLeftCenterCm * orientcos;

        if (!isnan(glLeftCentCorrCm))
        {
          //gl_pSerPort->printf("just before PIDCalcs call: WallTrackSetPoint  = %2.2f\n", WallTrackSetPoint);
          WallTrackOutput = PIDCalcs(glLeftCentCorrCm, WallTrackSetPoint, lastError, lastInput, lastIval, lastDerror,
            kp, ki, kd);

          //04/05/22 have to use local var here, as result could be negative
          int16_t leftSpdnum = MOTOR_SPEED_QTR + WallTrackOutput;
          int16_t rightSpdnum = MOTOR_SPEED_QTR - WallTrackOutput;

          //04/05/22 Left/rightSpdnum can be negative here - watch out!
          rightSpdnum = (rightSpdnum <= MOTOR_SPEED_HALF) ? rightSpdnum : MOTOR_SPEED_HALF; //result can still be neg
          glRightspeednum = (rightSpdnum > 0) ? rightSpdnum : 0; //result here must be positive
          leftSpdnum = (leftSpdnum <= MOTOR_SPEED_HALF) ? leftSpdnum : MOTOR_SPEED_HALF;//result can still be neg
          glLeftspeednum = (leftSpdnum > 0) ? leftSpdnum : 0; //result here must be positive

          MoveAhead(glLeftspeednum, glRightspeednum);

          gl_pSerPort->printf(WallFollowTelemStr, millis(),
            glLeftFrontCm, glLeftCenterCm, glLeftRearCm, 
            glLeftSteeringVal, orientdeg, orientcos, glLeftCentCorrCm,
            WallTrackSetPoint, lastError, WallTrackOutput,
            glLeftspeednum, glRightspeednum);
        }
      }
    }


    //09/29/22 if we get to here, hold in loop for user input
    mSecSinceLastWallTrackUpdate = 0;
    while (true)
    {
      CheckForUserInput();

      if (mSecSinceLastWallTrackUpdate >= 10 * WALL_TRACK_UPDATE_INTERVAL_MSEC)
      {
        mSecSinceLastWallTrackUpdate -= 10 * WALL_TRACK_UPDATE_INTERVAL_MSEC;
        gl_pSerPort->printf("After exit from TrackRightWallOffset\n");
      }
    }
  }

while (true)

{

//10/16/22 starting over with wall track tuning

float kp = WallTrack_Kp;

float ki = WallTrack_Ki;

float kd = WallTrack_Kd;

float lastError = 0;

float lastInput = 0;

float lastIval = 0;

float lastDerror = 0;

WallTrackSetPoint = OffCm; //04/17/22 this value holds robot parallel to left wall

gl_pSerPort->printf("\nTrackLeftWallOffset: Start tracking offset of %2.1fcm with Kp/Ki/Kd = %2.2f\t%2.2f\t%2.2f\n",

WallTrackSetPoint, kp, ki, kd);

gl_pSerPort->printf(WallFollowTelemHdrStr);

//Step4: Track the wall using PID algorithm

mSecSinceLastWallTrackUpdate = 0; //added 09/04/21

MsecSinceLastFrontDistUpdate = 0; //added 10/02/22 to slow front LIDAR update rate

while (true)

{

CheckForUserInput(); //this is a bit recursive, but should still work (I hope)

if (mSecSinceLastWallTrackUpdate > WALL_TRACK_UPDATE_INTERVAL_MSEC)

{

mSecSinceLastWallTrackUpdate -= WALL_TRACK_UPDATE_INTERVAL_MSEC;

//03/08/22 abstracted these calls to UpdateAllEnvironmentParameters()

UpdateAllEnvironmentParameters();//03/08/22 added to consolidate sensor update calls

//from Teensy_7VL53L0X_I2C_Slave_V3.ino: LeftSteeringVal = (LF_Dist_mm - LR_Dist_mm) / 100.f; //rev 06/21/20 see PPalace post

float orientdeg = GetWallOrientDeg(glLeftSteeringVal);

float orientrad = (PI / 180.f) * orientdeg;

float orientcos = cosf(orientrad);

glLeftCentCorrCm = glLeftCenterCm * orientcos;

if (!isnan(glLeftCentCorrCm))

{

//gl_pSerPort->printf("just before PIDCalcs call: WallTrackSetPoint = %2.2f\n", WallTrackSetPoint);

WallTrackOutput = PIDCalcs(glLeftCentCorrCm, WallTrackSetPoint, lastError, lastInput, lastIval, lastDerror,

kp, ki, kd);

//04/05/22 have to use local var here, as result could be negative

int16_t leftSpdnum = MOTOR_SPEED_QTR + WallTrackOutput;

int16_t rightSpdnum = MOTOR_SPEED_QTR - WallTrackOutput;

//04/05/22 Left/rightSpdnum can be negative here - watch out!

rightSpdnum = (rightSpdnum <= MOTOR_SPEED_HALF) ? rightSpdnum : MOTOR_SPEED_HALF; //result can still be neg

glRightspeednum = (rightSpdnum > 0) ? rightSpdnum : 0; //result here must be positive

leftSpdnum = (leftSpdnum <= MOTOR_SPEED_HALF) ? leftSpdnum : MOTOR_SPEED_HALF;//result can still be neg

glLeftspeednum = (leftSpdnum > 0) ? leftSpdnum : 0; //result here must be positive

MoveAhead(glLeftspeednum, glRightspeednum);

gl_pSerPort->printf(WallFollowTelemStr, millis(),

glLeftFrontCm, glLeftCenterCm, glLeftRearCm,

glLeftSteeringVal, orientdeg, orientcos, glLeftCentCorrCm,

WallTrackSetPoint, lastError, WallTrackOutput,

glLeftspeednum, glRightspeednum);

}

//09/29/22 if we get to here, hold in loop for user input

mSecSinceLastWallTrackUpdate = 0;

while (true)

{

CheckForUserInput();

if (mSecSinceLastWallTrackUpdate >= 10 * WALL_TRACK_UPDATE_INTERVAL_MSEC)

{

mSecSinceLastWallTrackUpdate -= 10 * WALL_TRACK_UPDATE_INTERVAL_MSEC;

gl_pSerPort->printf("After exit from TrackRightWallOffset\n");

}

The big change from previous versions was to go back to using the desired offset distance as the setpoint for the PID algorithm, and using the measured distance from the (left or right) center VL53L0X sensor as the input to be controlled. Now one might be excused from wondering why the heck I wasn’t doing this all along, as it does seem logical that if you want to control the robot’s distance from the near wall, you should use the desired distance as the setpoint and the measured distance as the input – duh!

Well, way back in the beginning of time, when I changed over from dual ultrasonic ‘Ping’ sensors to dual arrays of three VL53L0X LIDAR sensors well over 18 months ago, I wound up using a combination of the ‘steering value’ ( (front – rear)/100 ) and the reported center distance – desired offset as the input to the PID calc routine, as shown in the following code snippet:

	while (true)
	{
		CheckForUserInput(); //this is a bit recursive, but should still work (I hope)
 
		//now using TIMER5 100 mSec interrupt for timing
		if (bTimeForNavUpdate)
		{
			//sinceLastComputeTime -= WALL_TRACK_UPDATE_INTERVAL_MSEC;
			bTimeForNavUpdate = false;
 
			//GetRequestedVL53l0xValues(VL53L0X_LEFT); //now done in TIMER5 ISR
 
			//have to weight value by both angle and wall offset
			WallTrackSteerVal = LeftSteeringVal + (Lidar_LeftCenter - 10 * WALL_OFFSET_TGTDIST_CM) / 1000.f;
 
			//update motor speeds, skipping bad values
			if (!isnan(WallTrackSteerVal))
			{
				//10/12/20 now this executes every time, with interval controlled by timer ISR
				PIDCalcs(WallTrackSteerVal, WallTrackSetPoint, TIMER5_INTERVAL_MSEC, lastError, lastInput, lastIval, lastDerror,
					kp, ki, kd, WallTrackOutput);
				//PIDCalcs(WallTrackSteerVal, WallTrackSetPoint, WALL_TRACK_UPDATE_INTERVAL_MSEC, lastError, lastInput, lastIval, lastDerror,
				//	kp, ki, kd, WallTrackOutput);
 
				int speed = 0;
 
				int leftspeednum = MOTOR_SPEED_QTR + WallTrackOutput;
				int rightspeednum = MOTOR_SPEED_QTR - WallTrackOutput;
 
				rightspeednum = (rightspeednum <= MOTOR_SPEED_FULL) ? rightspeednum : MOTOR_SPEED_FULL;
				rightspeednum = (rightspeednum > 0) ? rightspeednum : 0;
				leftspeednum = (leftspeednum <= MOTOR_SPEED_FULL) ? leftspeednum : MOTOR_SPEED_FULL;
				leftspeednum = (leftspeednum > 0) ? leftspeednum : 0;
 
				MoveAhead(leftspeednum, rightspeednum);
 
				mySerial.printf("%lu \t%d\t%d\t%d \t%2.2f\t%2.2f\t%2.2f\t%2.2f \t%2.2f\t%2.2f\t%2.2f \t%2.2f\t%d\t%d\n",
					millis(),
					Lidar_LeftFront, Lidar_LeftCenter, Lidar_LeftRear,
					WallTrackSteerVal, WallTrackSetPoint, lastError, lastIval,
					kp * lastError, ki * lastIval, kd * lastDerror,
					WallTrackOutput, leftspeednum, rightspeednum);
			}
		}
	}

while (true)

{

CheckForUserInput(); //this is a bit recursive, but should still work (I hope)

//now using TIMER5 100 mSec interrupt for timing

if (bTimeForNavUpdate)

{

//sinceLastComputeTime -= WALL_TRACK_UPDATE_INTERVAL_MSEC;

bTimeForNavUpdate = false;

//GetRequestedVL53l0xValues(VL53L0X_LEFT); //now done in TIMER5 ISR

//have to weight value by both angle and wall offset

WallTrackSteerVal = LeftSteeringVal + (Lidar_LeftCenter - 10 * WALL_OFFSET_TGTDIST_CM) / 1000.f;

//update motor speeds, skipping bad values

if (!isnan(WallTrackSteerVal))

{

//10/12/20 now this executes every time, with interval controlled by timer ISR

PIDCalcs(WallTrackSteerVal, WallTrackSetPoint, TIMER5_INTERVAL_MSEC, lastError, lastInput, lastIval, lastDerror,

kp, ki, kd, WallTrackOutput);

//PIDCalcs(WallTrackSteerVal, WallTrackSetPoint, WALL_TRACK_UPDATE_INTERVAL_MSEC, lastError, lastInput, lastIval, lastDerror,

// kp, ki, kd, WallTrackOutput);

int speed = 0;

int leftspeednum = MOTOR_SPEED_QTR + WallTrackOutput;

int rightspeednum = MOTOR_SPEED_QTR - WallTrackOutput;

rightspeednum = (rightspeednum <= MOTOR_SPEED_FULL) ? rightspeednum : MOTOR_SPEED_FULL;

rightspeednum = (rightspeednum > 0) ? rightspeednum : 0;

leftspeednum = (leftspeednum <= MOTOR_SPEED_FULL) ? leftspeednum : MOTOR_SPEED_FULL;

leftspeednum = (leftspeednum > 0) ? leftspeednum : 0;

MoveAhead(leftspeednum, rightspeednum);

mySerial.printf("%lu \t%d\t%d\t%d \t%2.2f\t%2.2f\t%2.2f\t%2.2f \t%2.2f\t%2.2f\t%2.2f \t%2.2f\t%d\t%d\n",

millis(),

Lidar_LeftFront, Lidar_LeftCenter, Lidar_LeftRear,

WallTrackSteerVal, WallTrackSetPoint, lastError, lastIval,

kp * lastError, ki * lastIval, kd * lastDerror,

WallTrackOutput, leftspeednum, rightspeednum);

}

This is the line that calculates the input value to the PID:

//have to weight value by both angle and wall offset
WallTrackSteerVal = LeftSteeringVal + (Lidar_LeftCenter - 10 * WALL_OFFSET_TGTDIST_CM) / 1000.f;

1 2	//have to weight value by both angle and wall offset WallTrackSteerVal = LeftSteeringVal + (Lidar_LeftCenter - 10 * WALL_OFFSET_TGTDIST_CM) / 1000.f;

This actually worked pretty well, but as I discovered recently, it is very difficult to integrate two very different physical mechanisms in the same calculations – almost literally oranges and apples. When the offset is small, the steering value term dominates and the robot simply continues more or less – but not quite – parallel to the wall, meaning that it slowly diverges from the desired offset – getting closer or further away. When the divergence gets large enough the offset term dominates and the robot turns toward the desired offset, but it is almost impossible to get PID terms that are large enough to actually make corrections without being so large as to cause wild oscillations.

The above problem didn’t really come to a head until just recently when I started having problems with tracking where the robot started off at or close to the desired offset value and generally parallel, meaning both terms in the above expression were near zero – for this case the behavior was a bit erratic to say the least.

So, back to the basics. The following plot and short video show the robot’s behavior with the new setup (offset = 40cm, PID = (10,0,0)):

Tracking left wall with desired offset = 40cm

Desired offset = 40cm, PID = (10,0,0)

With this setup, the robot tracks the desired 40cm offset very well (average of 41.77cm), with a very slow oscillation. I’m sure I can tweak this up a bit with a slightly higher ‘P’ value and then adding a small amount of ‘I’, but even with the most basic parameter set the system is obviously stable.

20 October 2022 Update:

I made another run with PID(10,0,0), but this time I started the run with the robot displaced about 7cm from the 40cm offset. As shown in the plot and short video, this caused quite a large oscillation; not quite disastrous, but probably would have been if my test wall had been any longer.

PID(10,0,0) with robot initial distance from wall = 33cm

PID(10,0,0) with initial position at 33cm

After looking at the data from this run, I decided to try lowering the P value from 10 to 5, thinking that the lower value would reduce the oscillation magnitude with a non-zero initial displacement from the desired setpoint. As the following plot and short video shows, the result was much better.

221022 PID(5,0,0) init dist 33cm

So then I tried PID(3,0,0), again with an initial placement of 33cm from the wall, 7cm from the setpoint of 40cm

PID(3,0,0) init dist 33cm, avg for all points ~41.3cm

As shown by the plot and video, PID(3,0,0) does a very good job of recovering from the large initial offset and then maintaining the desired 40cm offset. This result makes me start to wonder if my separate ‘Approach and Capture’ stage is required at all. However, a subsequent run with PID (3,0,0) but with an initial placement of 15cm (25cm error) disabused me of any thoughts like that!

After talking this over with my PID-expert stepson, he recommended that I continue to decrease the ‘P’ term until the robot never quite gets to the desired setpoint before running out of room, and then adding some (possibly very small) amount of ‘D’ to hasten capture of the desired setpoint. So, I continued, starting with a ‘P’ value of 2, as shown below:

The ‘Err’ term is the actual PID error term, not multiplied by P as before

This result was a bit unexpected, as I thought such a ‘straight-line’ trajectory should have ended before going past the 40cm setpoint, indicating that I had achieved my ‘not quite controlling’ value of ‘P’. However, after thinking about a bit and looking at the actual data (shown below), I think what this shows is that the robot case is fundamentally different than most PID control applications in that reducing the error term (and thus the ‘drive’ signal) doesn’t necessarily change the robot’s trajectory, as the robot will tend to travel in a straight line in the absence of a contravening error term. In other words, removing the ‘drive’ due to the error term doesn’t cause the robot to slow down, as it would in a normal motor drive scenario.

Msec	LF	LC	LR	Steer	Deg	Cos	LCCorr	Set	Err	Output	LSpd	RSpd
105681	31	33	33	-0.28	-16	0.96	31.7	40	8.3	16.6	91	58
105781	30	33	32	-0.12	-6.86	0.99	32.8	40	7.2	14.5	89	60
105886	31	33	32	-0.07	-4	1	32.9	40	7.1	14.2	89	60
105980	31	33	34	-0.28	-16	0.96	31.7	40	8.3	16.6	91	58
106087	31	33	33	-0.19	-10.86	0.98	32.4	40	7.6	15.2	90	59
106182	32	34	33	-0.16	-9.14	0.99	33.6	40	6.4	12.9	87	62
106280	32	34	34	-0.16	-9.14	0.99	33.6	40	6.4	12.9	87	62
106388	33	34	33	-0.04	-2.29	1	34	40	6	12.1	87	62
106482	33	35	34	-0.04	-2.29	1	35	40	5	10.1	85	64
106589	34	37	36	-0.16	-9.14	0.99	36.5	40	3.5	6.9	81	68
106683	35	35	36	-0.07	-4	1	34.9	40	5.1	10.2	85	64
106781	36	38	36	-0.08	-4.57	1	37.9	40	2.1	4.2	79	70
106885	36	39	38	-0.26	-14.86	0.97	37.7	40	2.3	4.6	79	70
106981	37	38	39	-0.23	-13.14	0.97	37	40	3	6	80	69
107084	38	40	39	-0.12	-6.86	0.99	39.7	40	0.3	0.6	75	74
107179	38	42	41	-0.3	-17.14	0.96	40.1	40	-0.1	-0.3	74	75
107279	39	43	41	-0.22	-12.57	0.98	42	40	-2	-3.9	71	78
107388	40	43	41	-0.14	-8	0.99	42.6	40	-2.6	-5.2	69	80
107479	42	43	42	-0.03	-1.71	1	43	40	-3	-6	69	80
107586	42	46	44	-0.25	-14.29	0.97	44.6	40	-4.6	-9.2	65	84
107680	45	47	45	0.05	2.86	1	46.9	40	-6.9	-13.9	61	88
107780	44	49	47	-0.39	-22.29	0.93	45.3	40	-5.3	-10.7	64	85
107886	45	48	48	-0.27	-15.43	0.96	46.3	40	-6.3	-12.5	62	87
107979	47	49	50	-0.25	-14.29	0.97	47.5	40	-7.5	-15	60	89
108086	48	48	50	-0.31	-17.71	0.95	45.7	40	-5.7	-11.4	63	86
108179	48	49	51	-0.34	-19.43	0.94	46.2	40	-6.2	-12.4	62	87
108280	48	51	52	-0.35	-20	0.94	47.9	40	-7.9	-15.8	59	90
108384	49	50	53	-0.35	-20	0.94	47	40	-7	-14	61	88
108481	50	53	52	-0.16	-9.14	0.99	52.3	40	-12.3	-24.7	50	99
108586	51	53	52	-0.11	-6.29	0.99	52.7	40	-12.7	-25.4	49	100
108680	52	55	53	-0.13	-7.43	0.99	54.5	40	-14.5	-29.1	45	104
108781	50	54	55	-0.51	-29.14	0.87	47.2	40	-7.2	-14.3	60	89
108885	50	53	53	-0.21	-12	0.98	51.8	40	-11.8	-23.7	51	98
108978	52	55	56	-0.43	-24.57	0.91	50	40	-10	-20	54	95
109083	52	54	56	-0.4	-22.86	0.92	49.8	40	-9.8	-19.5	55	94
109181	52	54	55	-0.27	-15.43	0.96	52.1	40	-12.1	-24.1	50	99

Msec LF LC LR Steer Deg Cos LCCorr Set Err Output LSpd RSpd

105681 31 33 33 -0.28 -16 0.96 31.7 40 8.3 16.6 91 58

105781 30 33 32 -0.12 -6.86 0.99 32.8 40 7.2 14.5 89 60

105886 31 33 32 -0.07 -4 1 32.9 40 7.1 14.2 89 60

105980 31 33 34 -0.28 -16 0.96 31.7 40 8.3 16.6 91 58

106087 31 33 33 -0.19 -10.86 0.98 32.4 40 7.6 15.2 90 59

106182 32 34 33 -0.16 -9.14 0.99 33.6 40 6.4 12.9 87 62

106280 32 34 34 -0.16 -9.14 0.99 33.6 40 6.4 12.9 87 62

106388 33 34 33 -0.04 -2.29 1 34 40 6 12.1 87 62

106482 33 35 34 -0.04 -2.29 1 35 40 5 10.1 85 64

106589 34 37 36 -0.16 -9.14 0.99 36.5 40 3.5 6.9 81 68

106683 35 35 36 -0.07 -4 1 34.9 40 5.1 10.2 85 64

106781 36 38 36 -0.08 -4.57 1 37.9 40 2.1 4.2 79 70

106885 36 39 38 -0.26 -14.86 0.97 37.7 40 2.3 4.6 79 70

106981 37 38 39 -0.23 -13.14 0.97 37 40 3 6 80 69

107084 38 40 39 -0.12 -6.86 0.99 39.7 40 0.3 0.6 75 74

107179 38 42 41 -0.3 -17.14 0.96 40.1 40 -0.1 -0.3 74 75

107279 39 43 41 -0.22 -12.57 0.98 42 40 -2 -3.9 71 78

107388 40 43 41 -0.14 -8 0.99 42.6 40 -2.6 -5.2 69 80

107479 42 43 42 -0.03 -1.71 1 43 40 -3 -6 69 80

107586 42 46 44 -0.25 -14.29 0.97 44.6 40 -4.6 -9.2 65 84

107680 45 47 45 0.05 2.86 1 46.9 40 -6.9 -13.9 61 88

107780 44 49 47 -0.39 -22.29 0.93 45.3 40 -5.3 -10.7 64 85

107886 45 48 48 -0.27 -15.43 0.96 46.3 40 -6.3 -12.5 62 87

107979 47 49 50 -0.25 -14.29 0.97 47.5 40 -7.5 -15 60 89

108086 48 48 50 -0.31 -17.71 0.95 45.7 40 -5.7 -11.4 63 86

108179 48 49 51 -0.34 -19.43 0.94 46.2 40 -6.2 -12.4 62 87

108280 48 51 52 -0.35 -20 0.94 47.9 40 -7.9 -15.8 59 90

108384 49 50 53 -0.35 -20 0.94 47 40 -7 -14 61 88

108481 50 53 52 -0.16 -9.14 0.99 52.3 40 -12.3 -24.7 50 99

108586 51 53 52 -0.11 -6.29 0.99 52.7 40 -12.7 -25.4 49 100

108680 52 55 53 -0.13 -7.43 0.99 54.5 40 -14.5 -29.1 45 104

108781 50 54 55 -0.51 -29.14 0.87 47.2 40 -7.2 -14.3 60 89

108885 50 53 53 -0.21 -12 0.98 51.8 40 -11.8 -23.7 51 98

108978 52 55 56 -0.43 -24.57 0.91 50 40 -10 -20 54 95

109083 52 54 56 -0.4 -22.86 0.92 49.8 40 -9.8 -19.5 55 94

109181 52 54 55 -0.27 -15.43 0.96 52.1 40 -12.1 -24.1 50 99

23 October 2022 Update:

In previous work on this subject, I had already recognized that the ‘capture’ and ‘track’ phases of Wall-E’s behavior required separate treatment, and had implemented this with a ‘CaptureWallOffset()’ function to handle the ‘capture’ phase. This function calculates the amount of rotation needed to achieve an approximately 30 deg orientation angle with respect to the near wall, then moves forward to the desired wall offset value, and then turns back to parallel the near wall.

So, my next step is to re-integrate this ‘CaptureWallOffset()’ routine with my current distance-only based offset tracking algorithm. The idea is to essentially eliminate the problem space where the distance-only PID algorithm fails, so the PID only has to handle initial conditions very near the desired setpoint. When the ‘CaptureWallOffset()’ routine completes, the robot should be oriented parallel to the wall, and at a distance close to (but not necessarily the same as) the desired setpoint. Based on the above results, I think I will change the setpoint from the current constant value (40 cm at present) to match the measured distance from the wall at the point of ‘CaptureWallOffset()’ routine completion. This will guarantee that the PID starts out with the input matching the setpoint – i.e. zero error.

With this new setup, I made a run with the robot starting just 13cm from the wall. The CaptureWallOffset() routine moved the robot from the initial 13cm to about 37cm, with the robot ending up nearly parallel. The PID tracking algorithm started with an initial error term of +3.3, and tracked very well with a ‘P’ value of 10. See the plot and short video below. The video shows both the capture and track phases, but the plot only shows the track portion of the run.

PID tracking after completion of CaptureWallOffset()

Here’s a run with PID(3,0,0), starting at an offset of 22cm.

24 October 2022 Update:

While reading through some more PID theory/practice articles, I was once again reminded that smaller time intervals generally produce better results, and that struck a bit of a chord. Some time back I settled on a time interval of about 200mSec, but while I was working with my ‘WallTrackTuning_V2’ program I realized that this interval was due to the time required by the PulsedLight LIDAR to produce a front distance measurement. I discovered this when I tried to reduce the overall update time from 200 to 100mSec and got lots of errors from GetFrontDistCm(). After figuring this out, I modified the code to use a 200mSec time interval for the front LIDAR, and 100mSec for the VL53L0X side distance sensors.

So, it occurred to me that I might be able to reduce the side measurement interval even further, so I instrumented the robot to toggle a digital output (I borrowed the output for the red laser pointer) at the start and end of the wall tracking adjustment cycle, as shown in the code snippet below:

      if (mSecSinceLastWallTrackUpdate > WALL_TRACK_UPDATE_INTERVAL_MSEC)
      {
        digitalToggle(RED_LASER_DIODE_PIN); //10/24/22 toggle duration measurement pulse
        mSecSinceLastWallTrackUpdate -= WALL_TRACK_UPDATE_INTERVAL_MSEC;

        //03/08/22 abstracted these calls to UpdateAllEnvironmentParameters()
        UpdateAllEnvironmentParameters();//03/08/22 added to consolidate sensor update calls

        //from Teensy_7VL53L0X_I2C_Slave_V3.ino: LeftSteeringVal = (LF_Dist_mm - LR_Dist_mm) / 100.f; //rev 06/21/20 see PPalace post
        float orientdeg = GetWallOrientDeg(glLeftSteeringVal);
        float orientrad = (PI / 180.f) * orientdeg; 
        float orientcos = cosf(orientrad);
        glLeftCentCorrCm = glLeftCenterCm * orientcos;

        if (!isnan(glLeftCentCorrCm))
        {
          //gl_pSerPort->printf("just before PIDCalcs call: WallTrackSetPoint  = %2.2f\n", WallTrackSetPoint);
          WallTrackOutput = PIDCalcs(glLeftCentCorrCm, WallTrackSetPoint, lastError, lastInput, lastIval, lastDerror,
            kp, ki, kd);

          //04/05/22 have to use local var here, as result could be negative
          int16_t leftSpdnum = MOTOR_SPEED_QTR + WallTrackOutput;
          int16_t rightSpdnum = MOTOR_SPEED_QTR - WallTrackOutput;

          //04/05/22 Left/rightSpdnum can be negative here - watch out!
          rightSpdnum = (rightSpdnum <= MOTOR_SPEED_HALF) ? rightSpdnum : MOTOR_SPEED_HALF; //result can still be neg
          glRightspeednum = (rightSpdnum > 0) ? rightSpdnum : 0; //result here must be positive
          leftSpdnum = (leftSpdnum <= MOTOR_SPEED_HALF) ? leftSpdnum : MOTOR_SPEED_HALF;//result can still be neg
          glLeftspeednum = (leftSpdnum > 0) ? leftSpdnum : 0; //result here must be positive

          MoveAhead(glLeftspeednum, glRightspeednum);

          gl_pSerPort->printf(WallFollowTelemStr, millis(),
            glLeftFrontCm, glLeftCenterCm, glLeftRearCm, 
            glLeftSteeringVal, orientdeg, orientcos, glLeftCentCorrCm,
            WallTrackSetPoint, lastError, WallTrackOutput,
            glLeftspeednum, glRightspeednum);
        }
        digitalToggle(RED_LASER_DIODE_PIN); //10/24/22 toggle duration measurement pulse

if (mSecSinceLastWallTrackUpdate > WALL_TRACK_UPDATE_INTERVAL_MSEC)

{

digitalToggle(RED_LASER_DIODE_PIN); //10/24/22 toggle duration measurement pulse

mSecSinceLastWallTrackUpdate -= WALL_TRACK_UPDATE_INTERVAL_MSEC;

//03/08/22 abstracted these calls to UpdateAllEnvironmentParameters()

UpdateAllEnvironmentParameters();//03/08/22 added to consolidate sensor update calls

//from Teensy_7VL53L0X_I2C_Slave_V3.ino: LeftSteeringVal = (LF_Dist_mm - LR_Dist_mm) / 100.f; //rev 06/21/20 see PPalace post

float orientdeg = GetWallOrientDeg(glLeftSteeringVal);

float orientrad = (PI / 180.f) * orientdeg;

float orientcos = cosf(orientrad);

glLeftCentCorrCm = glLeftCenterCm * orientcos;

if (!isnan(glLeftCentCorrCm))

{

//gl_pSerPort->printf("just before PIDCalcs call: WallTrackSetPoint = %2.2f\n", WallTrackSetPoint);

WallTrackOutput = PIDCalcs(glLeftCentCorrCm, WallTrackSetPoint, lastError, lastInput, lastIval, lastDerror,

kp, ki, kd);

//04/05/22 have to use local var here, as result could be negative

int16_t leftSpdnum = MOTOR_SPEED_QTR + WallTrackOutput;

int16_t rightSpdnum = MOTOR_SPEED_QTR - WallTrackOutput;

//04/05/22 Left/rightSpdnum can be negative here - watch out!

rightSpdnum = (rightSpdnum <= MOTOR_SPEED_HALF) ? rightSpdnum : MOTOR_SPEED_HALF; //result can still be neg

glRightspeednum = (rightSpdnum > 0) ? rightSpdnum : 0; //result here must be positive

leftSpdnum = (leftSpdnum <= MOTOR_SPEED_HALF) ? leftSpdnum : MOTOR_SPEED_HALF;//result can still be neg

glLeftspeednum = (leftSpdnum > 0) ? leftSpdnum : 0; //result here must be positive

MoveAhead(glLeftspeednum, glRightspeednum);

gl_pSerPort->printf(WallFollowTelemStr, millis(),

glLeftFrontCm, glLeftCenterCm, glLeftRearCm,

glLeftSteeringVal, orientdeg, orientcos, glLeftCentCorrCm,

WallTrackSetPoint, lastError, WallTrackOutput,

glLeftspeednum, glRightspeednum);

}

digitalToggle(RED_LASER_DIODE_PIN); //10/24/22 toggle duration measurement pulse

Using my handy-dandy Hanmatek DSO, I was able to capture the pin activity, as shown in the following plot:

Wall track update cycle activity with 100mSec interval (20mSec/div)

As shown above, the update code takes a bit less than 20mSec to complete, and idles for the remaining 80mSec or so, waiting for the 100mSec time period to elapse. So, I should be able to reduce the time interval by at least a factor of two. I changed the update interval from 100mSec to 50mSec, and got the activity plot shown below:

Wall track update cycle activity with 50mSec interval (20mSec/div)

The above plot has the same 20mSec/div time scale as the previous one; as can be seen, there is still plenty of ‘idle’ time between wall tracking updates. Now to see if this actually changes the robot’s behavior.

As shown in the next plot and video, I ran another ‘sandbox’ test, this time with the update interval set to 50mSec vice 100mSec, and with an 11Cm initial offset.

PID(5,0,0), initial distance 11Cm

Then I ran it again, except this time with a PID of (10,0,0):

PID(10,0,0), initial distance 11Cm

This wasn’t at all what I expected. I thought the larger ‘P’ value would cause the robot to more closely track the desired offset, but that isn’t what happened. Everything is fine for the first two seconds (140,000 to 142,000 mSec), but then the robot starts weaving dramatically- to the point where the motor values max out at 127 on one side and 0 on the other – bummer. Looks like I need another consulting session with my PID wizard stepson!

25 October 2022 Update:

My PID wiz stepson liked my idea of breaking the wall tracking problem into an offset capture phase, followed by a wall tracking phase, but wasn’t particularly impressed with my thinking about reducing the PID update interval while simultaneously increasing the P value to 10, so, I’m back to taking more data. The following run is just the wall tracking phase, with 50mSec update interval and a P value of 3.

As can be seen, the robot doesn’t really make any corrections – just goes in a straight line more or less. However, the left/right wheel speed data does show the correct trend (left wheel drive decreasing, right wheel drive increasing), so maybe a non-zero ‘I’ value would do the trick?

Here’s a run with PID(3,0.5,0):

In the above plot the I value does indeed cause the robot to track back to the target distance, but then goes well past the target before starting to turn back. Too much I?

Here’s another run with PID(3,0.1,0) – looking pretty good!

This looks pretty good; with I = 0.1 the robot definitely adjusted back toward the target distance, but in a much smoother manner than with I = 0.5. OK, time to let the master view these results and see if I’m even in the right PID universe.

One thing to mention in these runs – they are performed in my office, and the total run length is a little over 2m (210Cm), so I’m only seeing just one correction maneuver. Maybe if I start out with a small offset from the target value? Nope – that won’t work – at least not tonight; my current code changes the setpoint from the entered value (40Cm in this case) to the actual offset value (36Cm on this run) before starting the run. Curses! Foiled again!

27 October 2022 Update:

Today I had some time to see how the PID handles wall-tracking runs starting with a small offset from the desired value. First I started with a run essentially identical to the last run from two days ago, just to make sure nothing significant had changed (shouldn’t, but who knows for sure), as shown below:

Then I tried a run with the same PID values, but with a small initial offset from the desired 40Cm:

As can be seen, the robot didn’t seem to handle this very well; there was an initial correction away from the wall (toward the desired offset), but the robot cruised well past the setpoint before correcting back toward the wall. This same behavior repeated when the robot went past the setpoint on the way back toward the wall.

To see which way I needed to move with the ‘I’ value, a made another run with the ‘I’ value changed from 0.1 to 0.25, as shown below:

Now the corrections were much more dramatic, and tracking was much less accurate. on the second correction (when the robot passed through the desired setpoint going away from the wall), the motor drive values maxed out (127 on the left, 0 on the right).

Next I tried an ‘I’ value of 0.05, as shown below:

This looks much nicer – deviations from the desired offset are much smaller, and everything is much smoother. However, I’m a little reluctant to declare victory here, as it may well be that the ‘I’ value is so small now that it may not be making any difference at all, and what I’m seeing is just the natural straight-line behavior of the robot. In addition, the robot may not be able to track the wall around some of the 45deg wall direction changes found in this house.

28 October 2022 Update:

I decided to rearrange my office ‘sandbox’ to provide additional running room for my wall-following robot. By setting up my sandbox ‘walls’ diagonally across my office, I was able to achieve a run length of almost 4 meters (3.94 to be exact). Here is a plot and short video from a run with PID(3,0.1,0):

I was very encouraged by this run. The robot tracked very well for most of the run, deviating slightly at the very end. I’m particularly pleased by the 1.4sec period from about 129400 (129.4sec) to about 130800 (130.8sec); during this period the left & right wheel motor drive values were pretty constant, indicating that the PID was actively controlling motor speeds to obtain the desired the wall offset. I’m not sure what caused the deviation at the end, but it might have something to do with the ‘wall’ material (black art board with white paper taped to the bottom half) in that section. However, after replacing that section with white foam core, the turn-out behavior persisted, so it wasn’t the wall properties causing the problem.

After looking at the data and the video for a while, I concluded that the divergence at the end of the run was real. During the first part of the run, the robot was close enough to the setpoint so that no significant correction was required. However, as soon as the natural straight-line behavior diverged enough from the set point to cause the PID to produce a non-small output, the tracking performance was seriously degraded. In other words, the PID was making things worse, not better – rats.

So, I tried another run, this time adding just a smidge of ‘D’, on the theory that this would still allow the PID to drive the robot back toward the setpoint, but not quite as wildly as before. With PID (3, 0.1, 0.1) I got the following plot:

As can be seen, things are quite a bit nicer, and the robot seemed to track fairly well for the entire 4m run.

Tried another run this morning with PID(3,0,0.1), i.e. removing the ‘I’ factor entirely, but leaving the ‘D’ parameter at 0.1 as in my last run yesterday. As can be seen in the following plot and short video, the results were very encouraging.

Made another run with ‘D’ bumped to 0.5 – looks even better.

Next, I investigated Wall-E3’s ability to handle wall angle changes. As the following plot and video shows, it actually does quite well with PID(3,0,0.5)

transients at end of run are due to encountering another angled wall – not shown in video

30 October 2022 Update

After a few more trials, I think I ended up with PID(3,0,1) as a reasonable compromise. With this setup, Wall-E3 can navigate both concave and convex wall angle changes, as shown in the following plot and short video.

As an aside, I also investigated several other PID triplets of the form (K*3,0,K*1) to see if other values of K besides 1 would produce the same behavior. At first I thought both K = 2 and K = 3 did well, but after a couple of trials I found myself back at K = 1. I’m not sure why there is anything magic about K = 1, but it’s hard to get around the fact that K = 2 and K = 3 did not work as well tracking my ‘sandbox’ walls.

At this point, I think it may be time to back-port the above results into my WallE3_AnomalyRecovery_V2.sln project, and then ultimately back into my main robot control project.

06 November 2022 Update:

Well, now I know why my past efforts at wall tracking didn’t rely exclusively on offset distance as measured by the 3 VL53L0X sensors on each side of the robot. The problem is that the reported distance is only accurate when the robot is parallel to the wall; any off-parallel orientation causes the reported distance to increase, even though the robot body is at the same distance. In the above work I thought I could beat this problem by compensating the distance measurement by the cosine of the off-parallel angle. This works (sort of) but causes the control loop to lag way behind what the robot is actually doing. Moreover, since there can be small variations in the distance reported by the VL53L0X array, the robot can be physically parallel to the wall while the sensors report an off-parallel orientation, or alternatively, the robot can be physically off-parallel (getting closer or farther away) to the wall, while the sensors report that it is parallel and consequently no correction is required. This is why, in previous versions, I tried to incorporate a absolute distance measurement along with orientation information into a single PID loop (didn’t work very well).

09 November 2022 Update:

After beating my head against the problem of tracking the nearby wall using a three-element array of VL53L0X distance sensors and a PID algorithm, I finally decided it just wasn’t wasn’t working well enough to rely on for generalized wall tracking. It does work, but has a pretty horrendous failure mode. If the robot ever gets past about 45 deg orientation w/r/t the near wall, the distance values from the VL53L0X sensor become invalid and the robot goes crazy.

So, I have been spending my night-time sleep preparation time (where I do some of my best thinking) trying to think of different ways of skinning this particular cat, as follows:

The robot needs to be able to accurately track a given offset
Must have enough agility to accommodate abrupt wall direction changes (90 deg changes are easy – but there are several 45 deg changes in our house)
Must handle obstacles appropriately.

It’s that first item on the list that I can’t seem to handle with the typical PID algorithm. So, I started to think about alternative schemes, and the one I decided to experiment with was the idea of implementing a zig-zag tracking algorithm using my already-proven SpinTurn() function. SpinTurn() uses relative heading output from my MP6050 MPU to implement CW/CCW turns, and has proven to be quite reliable (after Homer Creutz and I beat MPU6050 FIFO management into submission).

I modified one of my Wall Track Tuning programs to implement the ‘zig-zag’ algorithm, and ran some tests in my office ‘sandbox’. As the following Excel plot and short video shows, it actually did quite well, considering it was the product of a semi-dream state thought process!

As can be seen from the above, the robot did a decent job of tracking the desired 40Cm offset (average distance for the run was 39.75Cm), especially for the first iteration. I should be able to tweak the algorithm to track the wall faster and with less of a ‘drunken sailor’ behavior.

Stay tuned,

Frank

Additional Work on Wall Tracking Algorithm

Leave a reply

Posted 15 July 2022,

After getting everything working (or so I thought) in my sandbox, I started running into problems again with wall tracking. It just wasn’t very smooth at all. So, I decided to create a part-task version of my Wall-E3 code (WallE3_WallTrackTuning.ino) to just tackle PID tuning for left/right wall tracking. this version allows PID and offset values to be entered interactively to facilitate faster tuning. After a number of runs, I wound up with a PID set of (200,20,0). This produce a very nice, smooth tracking behavior.

In addition, I went back through all my code and re-educated myself on exactly how my current wall offset capture algorithm developed and whether or not it was, in fact, what I wanted. I started by diagramming all (I hope) relevant initial orientation and offset cases, as shown in the following Visio chart.

In the above figure, four basic configurations are diagrammed; The first two are for left-side tracking with the robot starting in three different configurations inside the desired 40cm tracking offset, and three more outside the tracking offset. The second two are the same as the first, but for right-side tracking.

The algorithm is based on knowing the robot’s orientation w/r/t the local wall, which is determined by the expression ‘Steer = (Front – Rear)/100’, implemented in the Teensy 3.5 MCU that manages the VL53L0X lidar array. This result is available to the main program as ‘glLeftSteeringVal’ and ‘glRightSteeringVal’. The steering values are proportional to the orientation angle in degrees, calculated as OrientDeg = steerval/0.0175.

Expressions for which way and how much to turn to achieve the desired capture approach angle of +/- 30 degrees were determined for each of the 12 starting configurations shown (numbered 1-12 in the above figure). An examination of the resulting expressions showed that they could be collapsed down into just two different calls to the ‘SpinTurn(isCCW, numdeg)’ subroutine – one for left-side tracking, and one for right-side tracking, as shown by the bold-face expressions above.

Wall-E3 Charging Station Integration, Part II

Leave a reply

Posted 28 May 2022

After getting the IR homing capability working with Wall-E3, I started working on the ability to recognize the charging beacon during normal wall-following operations, and then transitioning (or not, depending on battery level) to the charge station docking procedure.

The ‘transition-to-charge’ feature assumes that the robot is tracking the right-hand wall within a few meters of the charging station, and detects the beacon. To connect to the charger, the robot must first navigate away from the wall to a point on the IR beacon centerline, turn to line up with the beam, and then follow it to the charger.

As I was testing this feature, I noticed at one point the robot detected the IR beacon while tracking the wall opposite the charger, not the wall where the charger was installed. This is a real problem, because my current ‘transition-to-charger’ algorithm assumes the geometry associated with the common wall case. In the common wall case, the robot makes a 90 deg turn away from the wall and moves to a spot calculated to put it on the beam centerline, but this won’t work at all if the robot is starting from a point on the opposite wall. In that case, the robot needs to travel forward or backward parallel to the opposite wall by a distance calculated to put it on centerline. So, the first thing the robot needs to be able to do is to detect which case (common wall or opposite wall) it is dealing with.

The primary difference between the two cases is how much the robot has to turn away/toward the wall it is currently tracking in order to point directly at the beacon generator; if it is on the common wall, then it may not need to turn at all, or may even have to turn a bit toward the wall to point directly at the generator. If it is currently tracking the opposite wall however, it will have to turn 30-60 deg away from the wall. So, the determination as to which case is in play, the robot needs to measure the number of degrees of heading change required to face the charger; if the heading change is 30-60 degrees, then it is the opposite wall case. If it is just a few degrees, then it is the common wall case.

The following short video shows the two cases and the heading change required to point to the charger in each case.

Turn to beacon performance, for opposite and common wall cases

21 June 2022 Update:

Progress has been a bit slow over the last month, as I’ve been doing other things, including recovering from an eye/scalp injury sustained at the Senior Games in Florida (those old guys can still pack a wallop!). However, I now think I have the charging station homing operation working, at least for the right-wall-tracking (the most common and probably only) case.

As it turns out, I didn’t really need to worry about the problem of the robot picking up the IR homing beacon while tracking the far wall (i.e. the wall perpendicular to the one associated with the charging station). As I noted above, the robot can sometimes ‘see’ a beacon signal above the threshold, but when it does, the steering signal (goes from -1 to +1) is always off scale on one side or another. So, by adding the requirement that the steering signal be within the range of -0.8 to +0.8, this case is entirely eliminated, leaving only the ‘same-wall’ homing case – yay!

I made a number of improvements to the IR homing code, in particular the ‘initial approach’ code that places the robot optimally with respect to the IR beacon beam, so that the subsequent ‘home-to-charging-station’ procedure is almost always successful.

In the following short video, the robot tracks the opposite wall, makes the turn to track the adjacent wall, and then detects the IR homing beacon at the conclusion of the offset capture phase for the adjacent wall. Then the robot transitions to ‘I’m hungry – feed me’ mode.

In ‘feed me’ mode, the robot first aligns itself with the beacon in a two-stage (coarse and fine) procedure. Once this is accomplished, the robot determines its distance from the beacon, and then uses this information to determine how far off the adjacent wall it should be to perfectly line up with the center of the IR beam, makes a turn to be perpendicular to the adjacent wall, and then moves forward or backward to achieve the desired offset measurement. Once this is accomplished the robot re-aligns itself with the beacon again, using the same two-stage procedure. Once all this is done, the robot then homes on the beacon to connect to the charger.

The above algorithm is shown in action in the following short video. When viewing the video, keep the following in mind:

The homing beacon is only recognized at the conclusion of the wall offset capture maneuver for the adjacent wall, even though the IR beacon signal is above the threshold as soon as the robot make the turn to the adjacent wall. This is done to place the robot at a known location to start the process.
While aligning itself to the beacon, the robot turns ON its red laser pointer to allow us humans to follow the action. Although the ‘red’ laser looks mostly white in the video, it is indeed red.
The beacon alignment takes place in two stages – coarse, then fine. This can be see by the speed at which the red laser dot moves back and forth.
In this particular video, the robot is already at the proper wall offset, so the ‘move to desired rear distance’ operation is truncated – the robot makes the turn to be perpendicular to the wall, determines it is at the proper offset, and so immediately turns back to align to the beacon signal.

Successful ‘track and then home to charger’ run

Wall-E3 Charging Station Integration

Leave a reply

Posted 14 April 2022

Wall-E3 has a significantly different form-factor than Wall-E2, requiring modification of the lead-in rails on the charging station, as shown below.

Once the required mods were made, I uncommented ‘#define IR_HOMING_ONLY in my code to have Wall-E3 concentrate solely on homing to the charging station, and then worked my way into a set of PID values (100,0,30) that gave reasonable homing performance, as shown in the following short video:

And here’s an Excel plot showing typical homing performance.

24 April 2022 Update:

The above data and video was collected using the ‘NoPing’ version of the IR Homing algorithm, so I went back and did this again using the version that monitors the front distance, both for detecting a ‘stuck’ condition and for the ability to navigate around the charging station if a charge isn’t needed. Of course, this didn’t work right away for various reasons, but eventually I got it working and made another test run. Here’s a short slo-mo video, and the accompanying Excel chart showing homing performance.

IR Homing run in slo-mo with tracking status shown on rear panel LEDs

Steering value and front distance vs time

01 May 2022 Update:

Wall-E3 has made some significant progress in the last week, and is now capable of switching from right-wall tracking to IR Homing to the charging station, as shown in the following short video and telemetry output:

automatic switching from right-wall tracking to charging station homing

In TrackRightWallOffset with Kp/Ki/Kd = 400.00	0.00	0.00

In TrackRightWallOffset with RR/RC/RF = 20	18	19
straight window = 8 cm
GetWallOrientDeg(-0.0900): slopeval = 0.02, offparalleldeg -5.14
R/C/F dists = 20	18	19 Steerval = -0.090, WallAngle = -5.14, Inside
GetWallOrientDeg(0.4400): slopeval = 0.02, offparalleldeg 25.14
R/C/F dists = 20	20	24 Steerval = 0.440, WallOrientDeg = 25.14

approach start: orient angle = 25.143, tgt_distCm = 35
At start: meas_dist = 20, corr_dist = 18, err = prev_err = -17
GetWallOrientDeg(0.4800): slopeval = 0.02, offparalleldeg 27.43
R/C/F dists = 20	21	25 Steerval = 0.480, OrientDeg = 27.43, err/prev_err = -17
Msec	RFront	RCtr	RRear	ODeg	ORad	c_dist	Err	P_err
11065	26	22	20	27.4	0.5	18	-17	-17
11179	30	26	22	27.4	0.5	23	-12	-17
11293	33	28	25	27.4	0.5	24	-11	-12
11407	36	32	29	27.4	0.5	28	-7	-11
11521	40	35	31	27.4	0.5	31	-4	-7
11635	44	40	35	27.4	0.5	35	0	-4
At end of offset capture - prev_res*res = 0
correct back to parallel (Right side): RF/RC/RR/Orient = 44	40	35	27.43

TrackRightWallOffset: Start tracking offset of 40cm with Kp/Ki/Kd = 400.00	0.00	0.00
Msec	LF	LC	LR		RF	RC	RR		F	Fvar	R	Rvar	Steer	Set	Output	LSpd	RSpd
12235	728	112	816		41	39	38		104	11326	49	508	0.30	0.25	-20	94	55
12335	728	111	816		40	39	40		103	11536	56	479	0.01	0.25	96	0	127
12439	728	111	127		41	40	39		103	11730	57	452	0.23	0.25	 8	67	83
12539	728	111	816		41	39	40		103	11891	54	428	0.14	0.25	44	31	119
12637	728	111	816		42	39	40		101	12011	57	405	0.12	0.25	52	23	127
12736	728	110	816		43	42	39		100	12071	68	385	0.42	0.25	-68	127	7
12839	728	115	816		46	43	42		99	12052	75	370	0.47	0.25	-88	127	0
12936	728	109	816		47	45	42		91	11963	71	353	0.59	0.25	-136	127	0
13039	728	105	816		47	45	44		86	11772	79	342	0.45	0.25	-80	127	0
13138	111	113	123		48	45	43		80	11461	83	335	0.52	0.25	-108	127	0
13237	728	112	121		47	46	45		77	10997	76	323	0.40	0.25	-60	127	14
13336	728	117	126		48	46	46		76	10351	84	318	0.17	0.25	32	43	107
13437	728	794	126		50	49	49		76	9497	100	329	0.21	0.25	16	59	91
13537	728	794	816		47	48	49		71	9628	104	346	0.02	0.25	92	0	127
13635	113	111	816		47	46	47		67	9771	97	352	0.16	0.25	36	39	111
13738	107	794	816		46	44	46		64	9918	95	356	0.12	0.25	52	23	127
13836	728	794	816		44	43	43		61	10073	108	376	0.12	0.25	52	23	127
13935	728	794	125		44	42	43		57	10213	98	382	0.17	0.25	32	42	107
14036	728	112	816		44	42	42		55	10343	104	395	0.22	0.25	12	63	87
14134	728	119	816		44	41	41		50	10483	116	426	0.40	0.25	-60	127	14
14237	728	794	816		45	43	41		44	10637	121	463	0.50	0.25	-100	127	0
14338	106	98	125		46	43	41		38	10797	109	480	0.51	0.25	-104	127	0
In HandleAnomalousConditions with WALL_OFFSET_DIST_AHEAD error code detected
WALL_OFFSET_DIST_AHEAD case detected with tracking case Right
IRHomingValTotalAvg = 33711 
IR Beam Detected with Battery Voltage = 6.87
Low battery - homing to Charger
OK we have a IR Beacon, with front distance = 121!
In IRHomingNavigateToIAP with LF/LR/LS/RF/RR/RS = 728	816	-8.86	29	28	0.16
In IRHomingNavigateToIAP(Right) with LF/LR/LS/RF/RR/RS = 728	816	-8.86	30	27	0.26
IP is at 60 cm offset, 135 cm away from charging station, a ratio of 0.44
Robot is at 121 from charger, so we need a 53 cm offset
Current wall offset is 28 cm or 52% of required offset
offset is too small or too large - turn away from wall to adjust
After SpinTurn(), rear dist (cm) is 28
In MoveToDesiredRearDistCm(53) with Kp/Ki/Kd = 2.0/0.5/0.0
Msec	Rdist	TgtD	err	Ival	Out
19015	25	53	28.0	14.0	70.0
19215	32	53	21.0	24.5	66.5
19415	34	53	19.0	34.0	72.0
19615	47	53	6.0	37.0	49.0
19815	50	53	3.0	38.5	44.5
20015	62	53	-9.0	34.0	16.0
20215	60	53	-7.0	30.5	16.5
20415	70	53	-17.0	22.0	-12.0
20615	70	53	-17.0	13.5	-20.5
20815	63	53	-10.0	8.5	-11.5
21015	70	53	-17.0	0.0	-34.0
21215	62	53	-9.0	-4.5	-22.5
21415	66	53	-13.0	-11.0	-37.0
21615	57	53	-4.0	-13.0	-21.0
21815	62	53	-9.0	-17.5	-35.5
22015	51	53	2.0	-16.5	-12.5
22215	57	53	-4.0	-18.5	-26.5
22415	48	53	5.0	-16.0	-6.0
22615	55	53	-2.0	-17.0	-21.0
22815	48	53	5.0	-14.5	-4.5
23015	48	53	5.0	-12.0	-2.0
23215	53	53	0.0	-12.0	-12.0
Wall offset now 53 cm, with IRHomingValTotalAvg = 32824
TurnToHomingBeacon with IRAvg = 32705, Steering = 0.39 & IRRotate Kp,Ki,Kd = (40,10, 0)
TurnToHomingBeacon(RIGHT)


Msec	Signal	Steer	Val
25506	174.74	0.94	75
25627	-173.51	0.57	92
25746	-162.99	-0.03	94
25867	-152.65	-0.43	92
25986	-142.47	-0.67	54
26137	-129.94	-0.50	51
26256	-119.93	-1.00	7821
26377	-109.97	-0.99	19453
26496	-99.64	-0.90	33325
26617	-88.96	-0.83	40602
26738	-78.32	-0.72	47367
26857	-67.75	-0.46	55756
26978	-57.49	-0.01	67318
Coarse adjustment finished
Rotate back and forth as necessary to maximize received signal strength.
Start with CW rotation for trkside == TRACKING_RIGHT, and CCW for TRACKING_LEFT
Got 67510, 11448, 75232, 0.71 from IR Detector module


Msec	IRVal1	IRVal2	ValAvg	Steer	speed
28098	67460	11364	79224	0.71	-35
28196	66514	11494	78598	0.71	-42
28299	63398	12996	77744	0.66	-47
28397	60976	16642	77342	0.57	-49
28501	57878	23998	78631	0.41	-47
28598	46500	35428	80475	0.14	-37
28702	31442	45008	80086	-0.18	-23
28800	18736	49560	75560	-0.45	-7
28897	13184	51822	69920	-0.59	4
28999	12084	52470	65955	-0.63	11
29102	11924	52404	64633	-0.63	17
29198	11878	52354	64375	-0.63	24
29300	11922	52172	64222	-0.63	30
29399	13192	51606	64378	-0.59	35
29498	16370	50314	65195	-0.51	36
29601	21518	48806	67271	-0.39	35
29698	29220	46094	70776	-0.22	31
29803	37744	42130	75172	-0.05	25
TurnToHomingBeacon exited with Steering = -0.05
Should be close to beacon centerline val avg = 75172, SteeringVal = -0.055
IRHomeToChgStn with detection value = 80398, Steering = 0.09 & IRHOMING Kp,Ki,Kd = (75, 0,40)
front dist = 122, avoidance dist = 0

Time	BattV	Fin1	Fin2	Steer	PID_Out		LSpd	RSpd	FrontD	RearD
31939	6.86	47052	39000	0.09	-3.27		71	78	122	43
32036	6.77	47008	39042	0.09	-6.98		68	81	123	49
32137	6.83	47626	40062	0.09	-6.72		68	81	116	44
32237	6.75	48380	43116	0.06	-5.46		69	80	114	48
32337	6.82	50606	46486	0.04	-3.79		71	78	114	57
32438	6.85	53028	50760	0.02	-2.46		72	77	111	61
32537	6.85	55452	56032	-0.01	-0.69		74	75	104	60
32638	6.86	57998	61800	-0.03	1.32		76	73	100	64
32739	6.72	60542	68338	-0.06	3.39		78	71	97	75
32840	6.70	64942	74526	-0.07	4.82		79	70	95	80
32940	6.78	71884	79754	-0.05	4.57		79	70	90	75
33036	6.67	81310	84894	-0.02	2.83		77	72	86	81
33141	6.84	90606	92696	-0.01	1.26		76	73	83	89
33236	6.86	98940	101460	-0.01	0.90		75	74	79	89
33338	6.84	108390	112432	-0.02	1.14		76	73	75	90
33436	6.86	117900	124044	-0.03	1.62		76	73	69	104
33539	6.86	133920	136456	-0.01	1.34		76	73	66	110
33640	6.86	157150	150632	0.02	-0.37		74	75	61	103
33736	6.86	185900	168138	0.05	-2.60		72	77	58	109
33837	6.86	221118	193390	0.07	-4.35		70	79	52	123
33937	6.68	262698	222510	0.08	-5.57		69	80	48	123
34039	6.86	296898	256092	0.07	-5.90		69	80	40	750
34136	6.73	343506	290618	0.08	-5.87		69	80	35	750
34239	6.85	481186	345974	0.16	-9.06		65	84	26	819
34336	6.85	851810	480074	0.28	-16.31		58	91	20	819
34438	6.86	1434172	684000	0.35	-23.56		51	98	13	750
34538	6.77	2083914	1004848	0.35	-26.39		48	101	11	750
34638	6.85	2424412	1658876	0.19	-20.54		54	95	9	750
34737	6.84	2468376	2381848	0.02	-8.12		66	83	4	819
34838	6.94	2444718	2432648	0.00	-0.80		74	75	4	819
Charger Connected at 34839
Robot has successfully connected to charger!
Reset VL53L0X Teensy to reduce current consumption
ChgSec	BattV	TotalI	RunI	ChgI	RearD

0.0	6.9568	1.2419	0.4290	0.8129
0.1	6.9697	1.2355	0.3968	0.8387

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

In TrackRightWallOffset with Kp/Ki/Kd = 400.00 0.00 0.00

In TrackRightWallOffset with RR/RC/RF = 20 18 19

straight window = 8 cm

GetWallOrientDeg(-0.0900): slopeval = 0.02, offparalleldeg -5.14

R/C/F dists = 20 18 19 Steerval = -0.090, WallAngle = -5.14, Inside

GetWallOrientDeg(0.4400): slopeval = 0.02, offparalleldeg 25.14

R/C/F dists = 20 20 24 Steerval = 0.440, WallOrientDeg = 25.14

approach start: orient angle = 25.143, tgt_distCm = 35

At start: meas_dist = 20, corr_dist = 18, err = prev_err = -17

GetWallOrientDeg(0.4800): slopeval = 0.02, offparalleldeg 27.43

R/C/F dists = 20 21 25 Steerval = 0.480, OrientDeg = 27.43, err/prev_err = -17

Msec RFront RCtr RRear ODeg ORad c_dist Err P_err

11065 26 22 20 27.4 0.5 18 -17 -17

11179 30 26 22 27.4 0.5 23 -12 -17

11293 33 28 25 27.4 0.5 24 -11 -12

11407 36 32 29 27.4 0.5 28 -7 -11

11521 40 35 31 27.4 0.5 31 -4 -7

11635 44 40 35 27.4 0.5 35 0 -4

At end of offset capture - prev_res*res = 0

correct back to parallel (Right side): RF/RC/RR/Orient = 44 40 35 27.43

TrackRightWallOffset: Start tracking offset of 40cm with Kp/Ki/Kd = 400.00 0.00 0.00

Msec LF LC LR RF RC RR F Fvar R Rvar Steer Set Output LSpd RSpd

12235 728 112 816 41 39 38 104 11326 49 508 0.30 0.25 -20 94 55

12335 728 111 816 40 39 40 103 11536 56 479 0.01 0.25 96 0 127

12439 728 111 127 41 40 39 103 11730 57 452 0.23 0.25 8 67 83

12539 728 111 816 41 39 40 103 11891 54 428 0.14 0.25 44 31 119

12637 728 111 816 42 39 40 101 12011 57 405 0.12 0.25 52 23 127

12736 728 110 816 43 42 39 100 12071 68 385 0.42 0.25 -68 127 7

12839 728 115 816 46 43 42 99 12052 75 370 0.47 0.25 -88 127 0

12936 728 109 816 47 45 42 91 11963 71 353 0.59 0.25 -136 127 0

13039 728 105 816 47 45 44 86 11772 79 342 0.45 0.25 -80 127 0

13138 111 113 123 48 45 43 80 11461 83 335 0.52 0.25 -108 127 0

13237 728 112 121 47 46 45 77 10997 76 323 0.40 0.25 -60 127 14

13336 728 117 126 48 46 46 76 10351 84 318 0.17 0.25 32 43 107

13437 728 794 126 50 49 49 76 9497 100 329 0.21 0.25 16 59 91

13537 728 794 816 47 48 49 71 9628 104 346 0.02 0.25 92 0 127

13635 113 111 816 47 46 47 67 9771 97 352 0.16 0.25 36 39 111

13738 107 794 816 46 44 46 64 9918 95 356 0.12 0.25 52 23 127

13836 728 794 816 44 43 43 61 10073 108 376 0.12 0.25 52 23 127

13935 728 794 125 44 42 43 57 10213 98 382 0.17 0.25 32 42 107

14036 728 112 816 44 42 42 55 10343 104 395 0.22 0.25 12 63 87

14134 728 119 816 44 41 41 50 10483 116 426 0.40 0.25 -60 127 14

14237 728 794 816 45 43 41 44 10637 121 463 0.50 0.25 -100 127 0

14338 106 98 125 46 43 41 38 10797 109 480 0.51 0.25 -104 127 0

In HandleAnomalousConditions with WALL_OFFSET_DIST_AHEAD error code detected

WALL_OFFSET_DIST_AHEAD case detected with tracking case Right

IRHomingValTotalAvg = 33711

IR Beam Detected with Battery Voltage = 6.87

Low battery - homing to Charger

OK we have a IR Beacon, with front distance = 121!

In IRHomingNavigateToIAP with LF/LR/LS/RF/RR/RS = 728 816 -8.86 29 28 0.16

In IRHomingNavigateToIAP(Right) with LF/LR/LS/RF/RR/RS = 728 816 -8.86 30 27 0.26

IP is at 60 cm offset, 135 cm away from charging station, a ratio of 0.44

Robot is at 121 from charger, so we need a 53 cm offset

Current wall offset is 28 cm or 52% of required offset

offset is too small or too large - turn away from wall to adjust

After SpinTurn(), rear dist (cm) is 28

In MoveToDesiredRearDistCm(53) with Kp/Ki/Kd = 2.0/0.5/0.0

Msec Rdist TgtD err Ival Out

19015 25 53 28.0 14.0 70.0

19215 32 53 21.0 24.5 66.5

19415 34 53 19.0 34.0 72.0

19615 47 53 6.0 37.0 49.0

19815 50 53 3.0 38.5 44.5

20015 62 53 -9.0 34.0 16.0

20215 60 53 -7.0 30.5 16.5

20415 70 53 -17.0 22.0 -12.0

20615 70 53 -17.0 13.5 -20.5

20815 63 53 -10.0 8.5 -11.5

21015 70 53 -17.0 0.0 -34.0

21215 62 53 -9.0 -4.5 -22.5

21415 66 53 -13.0 -11.0 -37.0

21615 57 53 -4.0 -13.0 -21.0

21815 62 53 -9.0 -17.5 -35.5

22015 51 53 2.0 -16.5 -12.5

22215 57 53 -4.0 -18.5 -26.5

22415 48 53 5.0 -16.0 -6.0

22615 55 53 -2.0 -17.0 -21.0

22815 48 53 5.0 -14.5 -4.5

23015 48 53 5.0 -12.0 -2.0

23215 53 53 0.0 -12.0 -12.0

Wall offset now 53 cm, with IRHomingValTotalAvg = 32824

TurnToHomingBeacon with IRAvg = 32705, Steering = 0.39 & IRRotate Kp,Ki,Kd = (40,10, 0)

TurnToHomingBeacon(RIGHT)

Msec Signal Steer Val

25506 174.74 0.94 75

25627 -173.51 0.57 92

25746 -162.99 -0.03 94

25867 -152.65 -0.43 92

25986 -142.47 -0.67 54

26137 -129.94 -0.50 51

26256 -119.93 -1.00 7821

26377 -109.97 -0.99 19453

26496 -99.64 -0.90 33325

26617 -88.96 -0.83 40602

26738 -78.32 -0.72 47367

26857 -67.75 -0.46 55756

26978 -57.49 -0.01 67318

Coarse adjustment finished

Rotate back and forth as necessary to maximize received signal strength.

Start with CW rotation for trkside == TRACKING_RIGHT, and CCW for TRACKING_LEFT

Got 67510, 11448, 75232, 0.71 from IR Detector module

Msec IRVal1 IRVal2 ValAvg Steer speed

28098 67460 11364 79224 0.71 -35

28196 66514 11494 78598 0.71 -42

28299 63398 12996 77744 0.66 -47

28397 60976 16642 77342 0.57 -49

28501 57878 23998 78631 0.41 -47

28598 46500 35428 80475 0.14 -37

28702 31442 45008 80086 -0.18 -23

28800 18736 49560 75560 -0.45 -7

28897 13184 51822 69920 -0.59 4

28999 12084 52470 65955 -0.63 11

29102 11924 52404 64633 -0.63 17

29198 11878 52354 64375 -0.63 24

29300 11922 52172 64222 -0.63 30

29399 13192 51606 64378 -0.59 35

29498 16370 50314 65195 -0.51 36

29601 21518 48806 67271 -0.39 35

29698 29220 46094 70776 -0.22 31

29803 37744 42130 75172 -0.05 25

TurnToHomingBeacon exited with Steering = -0.05

Should be close to beacon centerline val avg = 75172, SteeringVal = -0.055

IRHomeToChgStn with detection value = 80398, Steering = 0.09 & IRHOMING Kp,Ki,Kd = (75, 0,40)

front dist = 122, avoidance dist = 0

Time BattV Fin1 Fin2 Steer PID_Out LSpd RSpd FrontD RearD

31939 6.86 47052 39000 0.09 -3.27 71 78 122 43

32036 6.77 47008 39042 0.09 -6.98 68 81 123 49

32137 6.83 47626 40062 0.09 -6.72 68 81 116 44

32237 6.75 48380 43116 0.06 -5.46 69 80 114 48

32337 6.82 50606 46486 0.04 -3.79 71 78 114 57

32438 6.85 53028 50760 0.02 -2.46 72 77 111 61

32537 6.85 55452 56032 -0.01 -0.69 74 75 104 60

32638 6.86 57998 61800 -0.03 1.32 76 73 100 64

32739 6.72 60542 68338 -0.06 3.39 78 71 97 75

32840 6.70 64942 74526 -0.07 4.82 79 70 95 80

32940 6.78 71884 79754 -0.05 4.57 79 70 90 75

33036 6.67 81310 84894 -0.02 2.83 77 72 86 81

33141 6.84 90606 92696 -0.01 1.26 76 73 83 89

33236 6.86 98940 101460 -0.01 0.90 75 74 79 89

33338 6.84 108390 112432 -0.02 1.14 76 73 75 90

33436 6.86 117900 124044 -0.03 1.62 76 73 69 104

33539 6.86 133920 136456 -0.01 1.34 76 73 66 110

33640 6.86 157150 150632 0.02 -0.37 74 75 61 103

33736 6.86 185900 168138 0.05 -2.60 72 77 58 109

33837 6.86 221118 193390 0.07 -4.35 70 79 52 123

33937 6.68 262698 222510 0.08 -5.57 69 80 48 123

34039 6.86 296898 256092 0.07 -5.90 69 80 40 750

34136 6.73 343506 290618 0.08 -5.87 69 80 35 750

34239 6.85 481186 345974 0.16 -9.06 65 84 26 819

34336 6.85 851810 480074 0.28 -16.31 58 91 20 819

34438 6.86 1434172 684000 0.35 -23.56 51 98 13 750

34538 6.77 2083914 1004848 0.35 -26.39 48 101 11 750

34638 6.85 2424412 1658876 0.19 -20.54 54 95 9 750

34737 6.84 2468376 2381848 0.02 -8.12 66 83 4 819

34838 6.94 2444718 2432648 0.00 -0.80 74 75 4 819

Charger Connected at 34839

Robot has successfully connected to charger!

Reset VL53L0X Teensy to reduce current consumption

ChgSec BattV TotalI RunI ChgI RearD

0.0 6.9568 1.2419 0.4290 0.8129

0.1 6.9697 1.2355 0.3968 0.8387

Stay tuned,

Frank

New Wall-Following Capability For Wall-E3

2 Replies

Posted 28 March, 2022

I’ve been working with Wall-E3, my new Teensy 3.5-powered autonomous wall-following robot. I’ve gotten left-wall and right-wall tracking working pretty well, but the transition from one wall to the next (typically right-angle) wall was pretty awkward. The robot basically ran right up to the next wall, stopped, backed up, and then made a right-angle turn to follow the next wall. So, I am trying to make that transition a bit smoother.

After trying a few different ideas, the one I settled on was to use my current very successful ‘SpinTurn()’ function to do the transition. I modified my ‘CheckForAnomalies()’ function to add a check for forward distance less than twice the desired offset distance. When this distance is detected, the robot stops and then makes a right-angle ‘spin’ turn (one sides wheels go forward, the other sides wheels go backward) in the direction away from the currently tracked wall, and then re-enters ‘Track’ mode causing it to track the next wall normally. Here’s a short video showing the process:

robot tracking left wall, then making a ‘spin’ turn to follow the next wall

Now that I have it working for left-wall tracking, it should be easy to port it to the right-wall tracking condition.

07 April 2022 Update:

Well, as usual, what I thought would be easy has turned out to be anything but. I was able to port the left wall tracking algorithm to the right side, but as I was testing the result, I noticed that Wall-E3 doesn’t really track the right (or left, for that matter) wall. After it ‘captures’ the desired wall offset and turns back to the parallel orientation, it basically goes straight ahead (same speed applied to both side’s motors). If the initial orientation is close to parallel, it looks like it is tracking, but it isn’t.

So, I tried a number of ideas to actually get it to track the desired offset, but they all resulted in poor-to-catastrophic tracking. After working the problem, I began to see that, as always, the issue is the errors associated with the VL53L0X sensor distance measurements. There are two distinct types of errors – an initial ‘calibration’ error associated with sensor-to-sensor variation, and the measurement error that occurs when the robot isn’t oriented parallel to the measured surface.

Calibration Errors:

Each individual VL53L0X sensor gets a slightly different value for the distance to the target, and sometimes ‘slightly’ can be pretty big – 2-3cm at 20cm, for instance. Up until now I had been ignoring these errors, but the time had come to do something about. So, as I always do when troubleshooting an issue, I started taking data. I ran a bunch of trials for all seven VL53L0X sensors at various distances. After gathering the data, I used Excel’s curve-fitting capability to fit a linear equation to the points, as shown below:

The linear-fit equations gave me a starting point, but they still had to be tweaked a bit to provide the best possible match between what the VL53L0X sensor reported and the actual measurement. Again I used Excel to tweak the equations to give the best match as shown below:

Left-side ‘tweaked’ correction expression

Right-side ‘tweaked’ correction expression

The expressions shown in red are the ones used to correct the VL53L0X-measured distances to be as close as possible to the actual distances (10cm, 20cm, 30cm).

The above corrections were coded into a set of seven ‘correction’ functions for the Teensy 3.5 program that manages the two VL53L0X arrays and the single VL53L0X rear distance sensor.

Correction functions in Teensy_7VL53L0X_I2C_Slave_V4.ino

While this did, indeed, solve a lot of problems – especially with the calculations for wall offset capture initial approach angle, it still didn’t entirely address Wall-E3’s inconsistent offset tracking performance.

Orientation Angle Induced Errors:

Wall-E3 tracks walls by offset by comparing the center VL53L0X measurement to the desired offset, and adjusting the left/right motor speeds to turn the robot in the desired direction. Unfortunately, the turn also throws off the measurements as now the sensors are pointing off-perpendicular, and return a different distance than the actual robot-to-wall perpendicular distance. I tried adjusting the PID controller algorithm to control the robot’s steering angle rather than the offset distance, and then calculating a new steering angle each time – this worked, but not very well.

So, the solution (I think) is to come up with a distance correction factor for off-perpendicular orientations. Going through the trigonometry, I came up with this expression:

corrdist=measdist*cos⁡(steeringAngle)

I programmed this into the following function:

uint16_t OrientCorr(uint16_t meas_dist, float steerval)
{
  //double corr_ang_rad = atan2(100*steerval,83.f); //83mm between front & rear sensors
  double corr_ang_rad = atan2(100*steerval,83.f); //83mm between front & rear sensors
  double corr_dist = meas_dist * cos(corr_ang_rad);

  myTeePrint.printf("OrientCorr: meas = %d, steer = %2.2f, corr_ang_rad = %2.2f, corr_dist = %2.2f\n", meas_dist, steerval, corr_ang_rad, corr_dist);

  return (uint16_t)round(corr_dist);
}

uint16_t OrientCorr(uint16_t meas_dist, float steerval)

{

//double corr_ang_rad = atan2(100*steerval,83.f); //83mm between front & rear sensors

double corr_ang_rad = atan2(100*steerval,83.f); //83mm between front & rear sensors

double corr_dist = meas_dist * cos(corr_ang_rad);

myTeePrint.printf("OrientCorr: meas = %d, steer = %2.2f, corr_ang_rad = %2.2f, corr_dist = %2.2f\n", meas_dist, steerval, corr_ang_rad, corr_dist);

return (uint16_t)round(corr_dist);

}

and then ran some tests to verify that the correction algorithm was having the desired effect. Here’s the setup:

and here are some Excel plots showing the results

Distance correction for off-perpendicular angles

As can be seen from the above plot, the corrected distance (gray curve) is pretty constant for angles of -30, 0 and +30 degrees.

09 April 2022 Update:

I have been thinking about the above orientation angle induced errors issue for a couple of days. I wasn’t really happy with that correction as shown in the above Excel plot, and it occurred to me that I didn’t really have to strictly abide by the above correction expression derived from the actual geometry. What I really wanted was a correction that would be accurate at low (or zero) offset angles, but would slightly over-correct for orientation angles in the +/- 30 deg range. In this way, when the PID engine adjusts the motor speeds to correct for an offset error, the system doesn’t try to run away. In fact, for a slight overcorrection algorithm, the center distance reported by the robot might actually go down rather than up for off-perpendicular angles. This would tend to make the PID think that it was over-correcting instead of under-correcting as it does with uncorrected distance reporting.

So, I went back to my test setup, and made some more measurements of corrected vs uncorrected center distances for -30, 0, and 30 degree orientations, for varying values of ‘tweak’ values in he correction expression, as shown in the Excel plots below:

Out of the above correction values, I like the “cos(1.1*corr_ang_rad)” configuration the best. The correction doesn’t modify the center distance at all for the parallel case, and produces a very slight over-correction at the +/- 30 degree orientation cases.

I added the ‘1.1*’ correction to the ‘OrientCorr()’ function and performed another right wall tracking test in my office ‘sandbox’ as shown in the short video below:

Right wall tracking with sensor calibration and orientation correction applied

Here is the telemetry output for this run:

In TrackRightWallOffset with Kp/Ki/Kd = 300.00	0.00	10.00

In TrackRightWallOffset with RR/RC/RF = 30	30	30
straight window = 8 cm
R/C/F dists = 30	30	30 Steerval = 0.020, WallAngle = 1.14, Inside
In SpinTurn(CCW, 28.86, 45.00)
R/C/F dists = 27	30	30 Steerval = 0.350, WallOrientDeg = 20.00

approach start: orient angle = 20.000, tgt_distCm = 40
At start - err = prev_err = -10
R/C/F dists = 27	30	30 Steerval = 0.350, OrientDeg = 20.00, err/prev_err = -10
R/C/F dists = 27	30	30 Steerval = 0.350, OrientDeg = 20.00, err/prev_err = -10
Msec	RFront	RCtr	RRear	Orient	Front	Rear	Err	P_err
68368: Error in GetFrontDistCm() - 0 replaced with 60
68384	31	30	28	17.1	118	46	-10	-10
68496	34	33	30	22.3	125	56	-7	-10
68609	36	36	32	24.0	119	60	-4	-7
68720	39	38	34	28.0	115	66	-2	-4
68831	44	41	36	44.0	108	68	1	-2
At end of offset capture - prev_res*res = -2
correct back to parallel (Right side): RF/RC/RR/Orient = 44	41	36	44.00
In SpinTurn(CW, 44.00, 30.00)

TrackRightWallOffset: Start tracking offset of 40.00cm with Kp/Ki/Kd = 300.00	0.00	10.00
Msec	LF	LC	LR		RF	RC	RR		F	Fvar	R	Rvar	Steer	Set	Output	LSpd	RSpd
69557	728	794	816		49	47	50		95	10899	73	39363	-0.10	-0.07	8.70	66	83
69657	728	794	816		50	51	52		99	10901	80	39332	-0.18	-0.11	20.60	54	95
69756	728	794	816		50	48	50		93	10910	86	39318	0.00	-0.08	-22.50	97	52
69858	728	794	816		49	46	48		90	10917	94	39277	0.09	-0.06	-44.30	119	30
69958	728	794	816		46	44	47		86	10927	87	39265	-0.10	-0.04	15.90	59	90
70055	728	114	816		44	45	45		76	10956	102	39252	-0.11	-0.05	18.00	57	93
70157	728	108	816		43	41	43		77	10976	819	48383	-0.02	-0.01	3.50	71	78
70255	728	109	816		39	38	40		74	10994	123	48334	-0.09	0.02	32.00	43	107
70357	109	99	816		36	36	38		70	11023	750	55303	-0.19	0.04	67.80	7	127
70455	112	103	816		34	33	34		65	11056	104	55318	-0.02	0.07	28.40	46	103
70557	728	116	816		29	30	31		55	11101	819	63702	-0.15	0.10	73.40	1	127
70655	728	120	816		27	27	28		48	11170	106	63708	-0.08	0.13	63.40	11	127
70757	728	794	816		24	24	25		43	11246	110	63715	-0.11	0.15	77.50	0	127
70854	728	794	816		22	22	24		37	11329	118	55334	-0.19	0.15	101.20	0	127
In HandleAnomalousConditions with WALL_OFFSET_DIST_AHEAD error code detected
WALL_OFFSET_DIST_AHEAD case detected with tracking case Neither
In SpinTurn(CCW, 90.00, 45.00)
71682: glLeftCenterCm = 794 glRightCenterCm = 25
glLeftCenterCm > glRightCenterCm --> Calling TrackRightWallOffset()
71686: TrackRightWallOffset(), glRightFrontCm = 26

In TrackRightWallOffset with Kp/Ki/Kd = 300.00	0.00	10.00

In TrackRightWallOffset with RR/RC/RF = 26	25	26
straight window = 8 cm
R/C/F dists = 26	25	26 Steerval = -0.060, WallAngle = -3.43, Inside
In SpinTurn(CCW, 33.43, 45.00)
R/C/F dists = 26	30	32 Steerval = 0.610, WallOrientDeg = 34.86

approach start: orient angle = 34.857, tgt_distCm = 40
At start - err = prev_err = -8
R/C/F dists = 26	30	32 Steerval = 0.610, OrientDeg = 34.86, err/prev_err = -8
R/C/F dists = 27	33	33 Steerval = 0.580, OrientDeg = 33.14, err/prev_err = -8
Msec	RFront	RCtr	RRear	Orient	Front	Rear	Err	P_err
72138	33	33	27	33.1	219	25	-7	-8
72254	40	38	31	40.0	195	29	-3	-7
72365	44	43	34	43.4	187	32	3	-3
At end of offset capture - prev_res*res = -9
correct back to parallel (Right side): RF/RC/RR/Orient = 44	43	34	43.43
In SpinTurn(CW, 43.43, 30.00)

TrackRightWallOffset: Start tracking offset of 40.00cm with Kp/Ki/Kd = 300.00	0.00	10.00
Msec	LF	LC	LR		RF	RC	RR		F	Fvar	R	Rvar	Steer	Set	Output	LSpd	RSpd
73091	110	112	122		40	38	39		151	11228	29	55621	0.09	0.02	-20.30	95	54
73189	728	110	816		39	40	41		153	11220	35	55688	-0.14	0.00	39.90	35	114
73291	728	112	816		40	38	39		150	11210	37	55762	0.18	0.02	-45.00	120	29
73394	728	111	816		40	38	39		146	11195	36	55854	0.06	0.02	-13.20	88	61
73492	114	115	120		38	37	38		141	11171	41	55917	0.07	0.03	-12.00	87	63
73589	728	113	816		38	38	38		134	11147	50	55921	-0.03	0.02	14.10	60	89
73692	728	116	816		36	37	36		129	11102	56	55913	0.05	0.03	-5.30	80	69
73789	112	115	816		36	35	36		124	11068	55	55971	0.00	0.05	14.30	60	89
73890	728	117	816		35	33	34		118	11028	64	56027	0.14	0.07	-19.80	94	55
73991	728	120	816		34	33	34		112	10988	69	56080	0.00	0.07	19.60	55	94
74090	728	120	816		34	33	32		109	10942	67	56165	0.11	0.07	-10.90	85	64
74189	728	122	816		33	32	32		103	10880	72	56246	0.06	0.08	5.40	69	80
74290	728	122	816		32	31	32		100	10825	85	56296	0.03	0.09	17.60	57	92
74393	728	794	816		32	30	31		92	10778	91	56321	0.10	0.10	0.60	74	75
74489	728	120	816		31	30	31		85	10736	86	56382	-0.01	0.10	31.90	43	106
74589	728	794	816		30	30	30		81	10687	92	56196	-0.01	0.10	33.00	42	108
74689	728	119	816		30	29	30		78	10611	104	56033	-0.01	0.11	35.90	39	110
74793	728	123	816		30	28	29		74	10519	107	55890	0.11	0.12	4.10	70	79
74890	728	122	816		30	29	29		71	10414	107	55749	0.12	0.11	-2.80	77	72
74990	728	794	816		31	29	29		67	10296	119	55629	0.20	0.11	-26.20	101	48
75089	728	115	816		31	30	29		63	10341	122	55523	0.15	0.10	-15.40	90	59
75189	728	119	816		31	31	30		59	10388	111	55452	0.09	0.09	-0.50	75	74
75290	728	115	816		32	31	30		52	10501	750	62042	0.20	0.09	-31.90	106	43
75392	728	119	816		33	31	30		47	10633	819	69966	0.30	0.09	-62.00	127	12
75490	728	123	816		32	32	31		40	10775	819	77492	0.12	0.08	-13.70	88	61
In HandleAnomalousConditions with WALL_OFFSET_DIST_AHEAD error code detected
WALL_OFFSET_DIST_AHEAD case detected with tracking case Neither
In SpinTurn(CCW, 90.00, 45.00)
76435: glLeftCenterCm = 794 glRightCenterCm = 26
glLeftCenterCm > glRightCenterCm --> Calling TrackRightWallOffset()
76440: TrackRightWallOffset(), glRightFrontCm = 27

In TrackRightWallOffset with Kp/Ki/Kd = 300.00	0.00	10.00

In TrackRightWallOffset with RR/RC/RF = 27	25	26
straight window = 8 cm
R/C/F dists = 27	25	26 Steerval = 0.010, WallAngle = 0.57, Inside
In SpinTurn(CCW, 29.43, 45.00)
R/C/F dists = 26	28	31 Steerval = 0.440, WallOrientDeg = 25.14

approach start: orient angle = 25.143, tgt_distCm = 40
At start - err = prev_err = -9
R/C/F dists = 26	28	31 Steerval = 0.440, OrientDeg = 25.14, err/prev_err = -9
R/C/F dists = 26	28	31 Steerval = 0.440, OrientDeg = 25.14, err/prev_err = -9
Msec	RFront	RCtr	RRear	Orient	Front	Rear	Err	P_err
76821: Error in GetFrontDistCm() - 0 replaced with 71
76832	32	31	26	33.7	159	40	-9	-9
76944	37	35	30	38.3	171	42	-5	-9
77059	41	39	33	42.3	167	46	-1	-5
77171	43	42	36	42.9	165	50	2	-1
At end of offset capture - prev_res*res = -2
correct back to parallel (Right side): RF/RC/RR/Orient = 43	42	36	42.86
In SpinTurn(CW, 42.86, 30.00)

TrackRightWallOffset: Start tracking offset of 40.00cm with Kp/Ki/Kd = 300.00	0.00	10.00
Msec	LF	LC	LR		RF	RC	RR		F	Fvar	R	Rvar	Steer	Set	Output	LSpd	RSpd
77927	728	794	816		42	41	41		116	10841	49	56047	0.08	-0.01	-26.10	101	48
78023	728	794	816		43	41	42		116	10846	46	56107	0.10	-0.01	-32.80	107	42
78126	728	794	816		42	41	45		119	10845	53	56159	-0.26	-0.01	71.40	3	127
78224	728	794	816		42	41	44		117	10841	58	56198	-0.21	-0.01	60.50	14	127
78326	728	794	816		39	39	38		109	10841	54	56270	0.11	0.01	-27.00	102	48
78427	728	794	816		38	36	37		101	10844	56	56357	0.08	0.04	-12.60	87	62
78525	728	794	816		37	35	36		96	10850	65	56427	0.12	0.05	-20.70	95	54
78623	728	794	816		36	36	34		91	10852	72	56493	0.21	0.04	-50.00	125	25
78726	728	794	816		35	35	35		87	10848	71	56543	0.01	0.05	9.90	65	84
78828	728	794	816		35	34	36		84	10841	78	56607	-0.13	0.06	55.50	19	127
78927	728	794	816		34	33	34		80	10836	90	47712	-0.07	0.07	42.50	32	117
79025	728	794	816		33	31	33		74	10836	94	47751	0.04	0.09	15.90	59	90
79124	728	794	816		32	31	31		71	10836	85	40235	0.04	0.09	15.00	60	90
79223	728	794	816		32	31	32		66	10839	103	40236	-0.03	0.09	35.30	39	110
79324	728	794	816		30	29	29		61	10845	110	30500	0.11	0.11	1.20	73	76
79424	728	794	816		30	30	29		56	10855	102	30502	0.18	0.10	-23.20	98	51
79523	728	794	816		31	30	29		50	10862	108	30502	0.27	0.10	-50.10	125	24
79625	728	794	816		31	30	29		43	10877	126	30505	0.21	0.10	-33.60	108	41
79725	728	794	816		31	30	29		38	10884	126	30344	0.18	0.10	-24.30	99	50
In HandleAnomalousConditions with WALL_OFFSET_DIST_AHEAD error code detected
WALL_OFFSET_DIST_AHEAD case detected with tracking case Neither
In SpinTurn(CCW, 90.00, 45.00)
80675: glLeftCenterCm = 794 glRightCenterCm = 24
glLeftCenterCm > glRightCenterCm --> Calling TrackRightWallOffset()
80680: TrackRightWallOffset(), glRightFrontCm = 25

In TrackRightWallOffset with Kp/Ki/Kd = 300.00	0.00	10.00

In TrackRightWallOffset with RR/RC/RF = 25	24	25
straight window = 8 cm
R/C/F dists = 25	24	25 Steerval = 0.050, WallAngle = 2.86, Inside
In SpinTurn(CCW, 27.14, 45.00)
R/C/F dists = 25	26	28 Steerval = 0.300, WallOrientDeg = 17.14

approach start: orient angle = 17.143, tgt_distCm = 40
At start - err = prev_err = -12
R/C/F dists = 25	26	28 Steerval = 0.300, OrientDeg = 17.14, err/prev_err = -12
R/C/F dists = 25	26	28 Steerval = 0.300, OrientDeg = 17.14, err/prev_err = -12
Msec	RFront	RCtr	RRear	Orient	Front	Rear	Err	P_err
81023: Error in GetFrontDistCm() - 0 replaced with 85
81031: Error in GetFrontDistCm() - 0 replaced with 85
81035	28	27	24	24.0	85	31	-13	-12
81151	32	32	27	31.4	205	40	-8	-13
81265	35	33	29	34.3	201	45	-7	-8
81378	38	36	31	38.3	196	49	-4	-7
81496	42	38	35	32.0	191	50	-2	-4
81611	45	44	38	17.7	189	55	2	-2
At end of offset capture - prev_res*res = -4
correct back to parallel (Right side): RF/RC/RR/Orient = 45	44	38	17.71
In SpinTurn(CW, 17.71, 30.00)

TrackRightWallOffset: Start tracking offset of 40.00cm with Kp/Ki/Kd = 300.00	0.00	10.00
Msec	LF	LC	LR		RF	RC	RR		F	Fvar	R	Rvar	Steer	Set	Output	LSpd	RSpd
82121	113	117	126		44	46	42		134	11189	51	30097	0.19	-0.06	-72.50	127	2
82221	109	111	127		46	45	43		129	11171	57	30079	0.25	-0.05	-89.50	127	0
82321	106	110	119		45	44	43		127	11143	58	30075	0.20	-0.04	-72.60	127	2
82419	108	111	115		46	46	47		127	11105	55	30075	-0.07	-0.06	0.50	74	75
82522	728	114	120		50	49	49		128	11055	61	30081	0.02	-0.09	-31.80	106	43
82621	112	116	816		50	47	50		109	11015	71	30077	-0.03	-0.07	-12.70	87	62
82721	728	794	816		48	46	52		104	10975	69	30073	-0.32	-0.06	75.00	0	127
82820	728	794	126		44	44	46		101	10930	73	30072	-0.18	-0.04	43.20	31	118
82919	728	794	816		43	42	43		110	10854	83	30074	0.05	-0.02	-18.90	93	56
83024	728	121	816		38	37	41		264	11010	82	30086	-0.29	0.03	92.10	0	127
83124	728	794	816		35	35	37		263	11116	83	30090	-0.18	0.05	69.90	5	127
83222	728	794	816		32	32	32		163	10944	85	30098	0.01	0.08	22.60	52	97
83319	728	794	816		30	30	32		87	10840	97	30103	-0.14	0.10	70.30	4	127
83421	728	794	128		30	29	30		82	10725	101	30106	-0.01	0.11	37.20	37	112
83520	728	124	816		29	27	27		81	10581	99	30110	0.18	0.13	-13.30	88	61
83621	728	122	816		28	27	28		77	10425	102	30115	-0.04	0.13	48.80	26	123
83720	728	123	816		28	27	26		73	10555	117	30114	0.17	0.13	-9.90	84	65
83819	728	117	816		28	28	28		68	10656	108	30115	0.05	0.12	19.90	55	94
83919	728	120	816		30	29	28		66	10746	750	30115	0.29	0.11	-51.50	126	23
84018	114	123	816		31	29	27		63	10839	819	30115	0.36	0.11	-74.30	127	0
84119	112	120	816		31	30	28		57	10950	819	30115	0.29	0.10	-57.60	127	17
84217	112	118	126		31	30	30		51	11065	750	37818	0.10	0.10	-1.90	76	73
84317	728	794	816		31	30	31		45	11196	750	45125	0.00	0.10	29.00	46	104
84418	728	122	127		31	29	29		39	11339	819	53775	0.18	0.11	-19.30	94	55

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

198

199

200

201

In TrackRightWallOffset with Kp/Ki/Kd = 300.00 0.00 10.00

In TrackRightWallOffset with RR/RC/RF = 30 30 30

straight window = 8 cm

R/C/F dists = 30 30 30 Steerval = 0.020, WallAngle = 1.14, Inside

In SpinTurn(CCW, 28.86, 45.00)

R/C/F dists = 27 30 30 Steerval = 0.350, WallOrientDeg = 20.00

approach start: orient angle = 20.000, tgt_distCm = 40

At start - err = prev_err = -10

R/C/F dists = 27 30 30 Steerval = 0.350, OrientDeg = 20.00, err/prev_err = -10

Msec RFront RCtr RRear Orient Front Rear Err P_err

68368: Error in GetFrontDistCm() - 0 replaced with 60

68384 31 30 28 17.1 118 46 -10 -10

68496 34 33 30 22.3 125 56 -7 -10

68609 36 36 32 24.0 119 60 -4 -7

68720 39 38 34 28.0 115 66 -2 -4

68831 44 41 36 44.0 108 68 1 -2

At end of offset capture - prev_res*res = -2

correct back to parallel (Right side): RF/RC/RR/Orient = 44 41 36 44.00

In SpinTurn(CW, 44.00, 30.00)

TrackRightWallOffset: Start tracking offset of 40.00cm with Kp/Ki/Kd = 300.00 0.00 10.00

Msec LF LC LR RF RC RR F Fvar R Rvar Steer Set Output LSpd RSpd

69557 728 794 816 49 47 50 95 10899 73 39363 -0.10 -0.07 8.70 66 83

69657 728 794 816 50 51 52 99 10901 80 39332 -0.18 -0.11 20.60 54 95

69756 728 794 816 50 48 50 93 10910 86 39318 0.00 -0.08 -22.50 97 52

69858 728 794 816 49 46 48 90 10917 94 39277 0.09 -0.06 -44.30 119 30

69958 728 794 816 46 44 47 86 10927 87 39265 -0.10 -0.04 15.90 59 90

70055 728 114 816 44 45 45 76 10956 102 39252 -0.11 -0.05 18.00 57 93

70157 728 108 816 43 41 43 77 10976 819 48383 -0.02 -0.01 3.50 71 78

70255 728 109 816 39 38 40 74 10994 123 48334 -0.09 0.02 32.00 43 107

70357 109 99 816 36 36 38 70 11023 750 55303 -0.19 0.04 67.80 7 127

70455 112 103 816 34 33 34 65 11056 104 55318 -0.02 0.07 28.40 46 103

70557 728 116 816 29 30 31 55 11101 819 63702 -0.15 0.10 73.40 1 127

70655 728 120 816 27 27 28 48 11170 106 63708 -0.08 0.13 63.40 11 127

70757 728 794 816 24 24 25 43 11246 110 63715 -0.11 0.15 77.50 0 127

70854 728 794 816 22 22 24 37 11329 118 55334 -0.19 0.15 101.20 0 127

In HandleAnomalousConditions with WALL_OFFSET_DIST_AHEAD error code detected

WALL_OFFSET_DIST_AHEAD case detected with tracking case Neither

In SpinTurn(CCW, 90.00, 45.00)

71682: glLeftCenterCm = 794 glRightCenterCm = 25

glLeftCenterCm > glRightCenterCm --> Calling TrackRightWallOffset()

71686: TrackRightWallOffset(), glRightFrontCm = 26

In TrackRightWallOffset with Kp/Ki/Kd = 300.00 0.00 10.00

In TrackRightWallOffset with RR/RC/RF = 26 25 26

straight window = 8 cm

R/C/F dists = 26 25 26 Steerval = -0.060, WallAngle = -3.43, Inside

In SpinTurn(CCW, 33.43, 45.00)

R/C/F dists = 26 30 32 Steerval = 0.610, WallOrientDeg = 34.86

approach start: orient angle = 34.857, tgt_distCm = 40

At start - err = prev_err = -8

R/C/F dists = 26 30 32 Steerval = 0.610, OrientDeg = 34.86, err/prev_err = -8

R/C/F dists = 27 33 33 Steerval = 0.580, OrientDeg = 33.14, err/prev_err = -8

Msec RFront RCtr RRear Orient Front Rear Err P_err

72138 33 33 27 33.1 219 25 -7 -8

72254 40 38 31 40.0 195 29 -3 -7

72365 44 43 34 43.4 187 32 3 -3

At end of offset capture - prev_res*res = -9

correct back to parallel (Right side): RF/RC/RR/Orient = 44 43 34 43.43

In SpinTurn(CW, 43.43, 30.00)

TrackRightWallOffset: Start tracking offset of 40.00cm with Kp/Ki/Kd = 300.00 0.00 10.00

Msec LF LC LR RF RC RR F Fvar R Rvar Steer Set Output LSpd RSpd

73091 110 112 122 40 38 39 151 11228 29 55621 0.09 0.02 -20.30 95 54

73189 728 110 816 39 40 41 153 11220 35 55688 -0.14 0.00 39.90 35 114

73291 728 112 816 40 38 39 150 11210 37 55762 0.18 0.02 -45.00 120 29

73394 728 111 816 40 38 39 146 11195 36 55854 0.06 0.02 -13.20 88 61

73492 114 115 120 38 37 38 141 11171 41 55917 0.07 0.03 -12.00 87 63

73589 728 113 816 38 38 38 134 11147 50 55921 -0.03 0.02 14.10 60 89

73692 728 116 816 36 37 36 129 11102 56 55913 0.05 0.03 -5.30 80 69

73789 112 115 816 36 35 36 124 11068 55 55971 0.00 0.05 14.30 60 89

73890 728 117 816 35 33 34 118 11028 64 56027 0.14 0.07 -19.80 94 55

73991 728 120 816 34 33 34 112 10988 69 56080 0.00 0.07 19.60 55 94

74090 728 120 816 34 33 32 109 10942 67 56165 0.11 0.07 -10.90 85 64

74189 728 122 816 33 32 32 103 10880 72 56246 0.06 0.08 5.40 69 80

74290 728 122 816 32 31 32 100 10825 85 56296 0.03 0.09 17.60 57 92

74393 728 794 816 32 30 31 92 10778 91 56321 0.10 0.10 0.60 74 75

74489 728 120 816 31 30 31 85 10736 86 56382 -0.01 0.10 31.90 43 106

74589 728 794 816 30 30 30 81 10687 92 56196 -0.01 0.10 33.00 42 108

74689 728 119 816 30 29 30 78 10611 104 56033 -0.01 0.11 35.90 39 110

74793 728 123 816 30 28 29 74 10519 107 55890 0.11 0.12 4.10 70 79

74890 728 122 816 30 29 29 71 10414 107 55749 0.12 0.11 -2.80 77 72

74990 728 794 816 31 29 29 67 10296 119 55629 0.20 0.11 -26.20 101 48

75089 728 115 816 31 30 29 63 10341 122 55523 0.15 0.10 -15.40 90 59

75189 728 119 816 31 31 30 59 10388 111 55452 0.09 0.09 -0.50 75 74

75290 728 115 816 32 31 30 52 10501 750 62042 0.20 0.09 -31.90 106 43

75392 728 119 816 33 31 30 47 10633 819 69966 0.30 0.09 -62.00 127 12

75490 728 123 816 32 32 31 40 10775 819 77492 0.12 0.08 -13.70 88 61

In HandleAnomalousConditions with WALL_OFFSET_DIST_AHEAD error code detected

WALL_OFFSET_DIST_AHEAD case detected with tracking case Neither

In SpinTurn(CCW, 90.00, 45.00)

76435: glLeftCenterCm = 794 glRightCenterCm = 26

glLeftCenterCm > glRightCenterCm --> Calling TrackRightWallOffset()

76440: TrackRightWallOffset(), glRightFrontCm = 27

In TrackRightWallOffset with Kp/Ki/Kd = 300.00 0.00 10.00

In TrackRightWallOffset with RR/RC/RF = 27 25 26

straight window = 8 cm

R/C/F dists = 27 25 26 Steerval = 0.010, WallAngle = 0.57, Inside

In SpinTurn(CCW, 29.43, 45.00)

R/C/F dists = 26 28 31 Steerval = 0.440, WallOrientDeg = 25.14

approach start: orient angle = 25.143, tgt_distCm = 40

At start - err = prev_err = -9

R/C/F dists = 26 28 31 Steerval = 0.440, OrientDeg = 25.14, err/prev_err = -9

Msec RFront RCtr RRear Orient Front Rear Err P_err

76821: Error in GetFrontDistCm() - 0 replaced with 71

76832 32 31 26 33.7 159 40 -9 -9

76944 37 35 30 38.3 171 42 -5 -9

77059 41 39 33 42.3 167 46 -1 -5

77171 43 42 36 42.9 165 50 2 -1

At end of offset capture - prev_res*res = -2

correct back to parallel (Right side): RF/RC/RR/Orient = 43 42 36 42.86

In SpinTurn(CW, 42.86, 30.00)

TrackRightWallOffset: Start tracking offset of 40.00cm with Kp/Ki/Kd = 300.00 0.00 10.00

Msec LF LC LR RF RC RR F Fvar R Rvar Steer Set Output LSpd RSpd

77927 728 794 816 42 41 41 116 10841 49 56047 0.08 -0.01 -26.10 101 48

78023 728 794 816 43 41 42 116 10846 46 56107 0.10 -0.01 -32.80 107 42

78126 728 794 816 42 41 45 119 10845 53 56159 -0.26 -0.01 71.40 3 127

78224 728 794 816 42 41 44 117 10841 58 56198 -0.21 -0.01 60.50 14 127

78326 728 794 816 39 39 38 109 10841 54 56270 0.11 0.01 -27.00 102 48

78427 728 794 816 38 36 37 101 10844 56 56357 0.08 0.04 -12.60 87 62

78525 728 794 816 37 35 36 96 10850 65 56427 0.12 0.05 -20.70 95 54

78623 728 794 816 36 36 34 91 10852 72 56493 0.21 0.04 -50.00 125 25

78726 728 794 816 35 35 35 87 10848 71 56543 0.01 0.05 9.90 65 84

78828 728 794 816 35 34 36 84 10841 78 56607 -0.13 0.06 55.50 19 127

78927 728 794 816 34 33 34 80 10836 90 47712 -0.07 0.07 42.50 32 117

79025 728 794 816 33 31 33 74 10836 94 47751 0.04 0.09 15.90 59 90

79124 728 794 816 32 31 31 71 10836 85 40235 0.04 0.09 15.00 60 90

79223 728 794 816 32 31 32 66 10839 103 40236 -0.03 0.09 35.30 39 110

79324 728 794 816 30 29 29 61 10845 110 30500 0.11 0.11 1.20 73 76

79424 728 794 816 30 30 29 56 10855 102 30502 0.18 0.10 -23.20 98 51

79523 728 794 816 31 30 29 50 10862 108 30502 0.27 0.10 -50.10 125 24

79625 728 794 816 31 30 29 43 10877 126 30505 0.21 0.10 -33.60 108 41

79725 728 794 816 31 30 29 38 10884 126 30344 0.18 0.10 -24.30 99 50

In HandleAnomalousConditions with WALL_OFFSET_DIST_AHEAD error code detected

WALL_OFFSET_DIST_AHEAD case detected with tracking case Neither

In SpinTurn(CCW, 90.00, 45.00)

80675: glLeftCenterCm = 794 glRightCenterCm = 24

glLeftCenterCm > glRightCenterCm --> Calling TrackRightWallOffset()

80680: TrackRightWallOffset(), glRightFrontCm = 25

In TrackRightWallOffset with Kp/Ki/Kd = 300.00 0.00 10.00

In TrackRightWallOffset with RR/RC/RF = 25 24 25

straight window = 8 cm

R/C/F dists = 25 24 25 Steerval = 0.050, WallAngle = 2.86, Inside

In SpinTurn(CCW, 27.14, 45.00)

R/C/F dists = 25 26 28 Steerval = 0.300, WallOrientDeg = 17.14

approach start: orient angle = 17.143, tgt_distCm = 40

At start - err = prev_err = -12

R/C/F dists = 25 26 28 Steerval = 0.300, OrientDeg = 17.14, err/prev_err = -12

Msec RFront RCtr RRear Orient Front Rear Err P_err

81023: Error in GetFrontDistCm() - 0 replaced with 85

81031: Error in GetFrontDistCm() - 0 replaced with 85

81035 28 27 24 24.0 85 31 -13 -12

81151 32 32 27 31.4 205 40 -8 -13

81265 35 33 29 34.3 201 45 -7 -8

81378 38 36 31 38.3 196 49 -4 -7

81496 42 38 35 32.0 191 50 -2 -4

81611 45 44 38 17.7 189 55 2 -2

At end of offset capture - prev_res*res = -4

correct back to parallel (Right side): RF/RC/RR/Orient = 45 44 38 17.71

In SpinTurn(CW, 17.71, 30.00)

TrackRightWallOffset: Start tracking offset of 40.00cm with Kp/Ki/Kd = 300.00 0.00 10.00

Msec LF LC LR RF RC RR F Fvar R Rvar Steer Set Output LSpd RSpd

82121 113 117 126 44 46 42 134 11189 51 30097 0.19 -0.06 -72.50 127 2

82221 109 111 127 46 45 43 129 11171 57 30079 0.25 -0.05 -89.50 127 0

82321 106 110 119 45 44 43 127 11143 58 30075 0.20 -0.04 -72.60 127 2

82419 108 111 115 46 46 47 127 11105 55 30075 -0.07 -0.06 0.50 74 75

82522 728 114 120 50 49 49 128 11055 61 30081 0.02 -0.09 -31.80 106 43

82621 112 116 816 50 47 50 109 11015 71 30077 -0.03 -0.07 -12.70 87 62

82721 728 794 816 48 46 52 104 10975 69 30073 -0.32 -0.06 75.00 0 127

82820 728 794 126 44 44 46 101 10930 73 30072 -0.18 -0.04 43.20 31 118

82919 728 794 816 43 42 43 110 10854 83 30074 0.05 -0.02 -18.90 93 56

83024 728 121 816 38 37 41 264 11010 82 30086 -0.29 0.03 92.10 0 127

83124 728 794 816 35 35 37 263 11116 83 30090 -0.18 0.05 69.90 5 127

83222 728 794 816 32 32 32 163 10944 85 30098 0.01 0.08 22.60 52 97

83319 728 794 816 30 30 32 87 10840 97 30103 -0.14 0.10 70.30 4 127

83421 728 794 128 30 29 30 82 10725 101 30106 -0.01 0.11 37.20 37 112

83520 728 124 816 29 27 27 81 10581 99 30110 0.18 0.13 -13.30 88 61

83621 728 122 816 28 27 28 77 10425 102 30115 -0.04 0.13 48.80 26 123

83720 728 123 816 28 27 26 73 10555 117 30114 0.17 0.13 -9.90 84 65

83819 728 117 816 28 28 28 68 10656 108 30115 0.05 0.12 19.90 55 94

83919 728 120 816 30 29 28 66 10746 750 30115 0.29 0.11 -51.50 126 23

84018 114 123 816 31 29 27 63 10839 819 30115 0.36 0.11 -74.30 127 0

84119 112 120 816 31 30 28 57 10950 819 30115 0.29 0.10 -57.60 127 17

84217 112 118 126 31 30 30 51 11065 750 37818 0.10 0.10 -1.90 76 73

84317 728 794 816 31 30 31 45 11196 750 45125 0.00 0.10 29.00 46 104

84418 728 122 127 31 29 29 39 11339 819 53775 0.18 0.11 -19.30 94 55

Looking at the video and the telemetry, the first leg starts with the normal offset capture maneuver, which ends with the robot about 44cm from the wall. Then it makes a pretty distinct correction toward the wall, overshoots the desired offset, and winds up the leg at about 22cm from the wall.

The second leg again starts with a capture maneuver to about 43cm. Then it stabilizes at about 32cm from the wall – nice.

The third leg maneuvers to about 43cm, and then again stabilizes at about 30cm.

The fourth leg was a bit anomalous, as it appeared to way overcorrect after capturing the desired 40cm offset, but I couldn’t find anything in the telemetry to explain it. It’s a mystery!

It’s clear from the above that I no longer need to correct for orientation angle induced errors during the offset maneuver, as these are now handled by my recent ‘global’ correction code. This will probably help with subsequent offset tracking, as the initial offset should be closer to the offset target at the start of the tracking phase. We’ll see…

After a number of trial runs, I finally settled (as much as anything is ‘settled’ in the Wall-E world) on PID = (400,5,40). Here’s a short video showing performance in this configuration:

And, once again, I still have to port this configuration and code back to the left-side wall tracking configuration. Here’s a short video of left-side wall tracking. Interestingly, my ‘random walk’ PID tuning technique resulted in significantly different PID values (300,0,200) vs (400,5,40) than the right side. No clue why.

At this point, I believe I have gone about as far as I can at the moment for wall tracking. WallE3 now can consistently track the walls in my office ‘sandbox’ using either the left-side or the right-side wall for reference. My plan going forward is to ‘archive’ this version (WallE3_WallTrack_V5) by copying it to a new project. The new project will have the goal of integrating charging station homing/connection into the system.

In preparation, I recently modified the charging station lead-in structure to accommodate the wider wheelbase on WallE3, as shown in the following photo:

17 April 2022 Update:

Well, I spoke too soon when I said above that wall-tracking was “settled”. I ran into a couple of significant problems; first, when the robot is already close to the proper offset, it is supposed to just turn to parallel the wall and then go into tracking mode, but on a number of occasions Wall-E3 ran out of control into the next wall. Secondly, wall tracking was anything but smooth, and I couldn’t get it to reliably track the desired offset. So, back to the drawing board (again).

The ‘close enough’ failures were being caused by a flaw in the ‘RotateToParallelOrientation() routine; as the robot approached the parallel orientation, the PID controller also started slowing the rotation speed, to the point where the robot wasn’t rotating anymore – just going straight ahead. If the actual parallel orientation wasn’t reached, the robot just kept going straight ahead forever – oops! The fix for this was to abandon the RotateToParallelOrientation() subroutine entirely, and just use WallOrientDeg() to get the current angular offset from parallel, and SpinTurn() to turn that angular amount back to parallel. RotateToParallelOrientation() is only used in two places (TrackRight/LeftWallOffset()), so the entire function can be removed as well.

The issue with offset tracking continues to bedevil me. When the robot is turned to approach the offset, the measured distances go the wrong way, so the PID tends to ‘wind up’ and drive the robot toward or away from the wall, rather than smoothly approaching the offset. I thought I had the answer to this by ‘tweaking’ the distance corrections due to off-parallel angles, but sadly, this did not help.

So, I removed the off-angle distance correction and went back to just tracking the steering angle – a value proportional to the difference between the front and rear side distance measurements. Now tracking was much more stable, but the robot traveled in a straight line slightly toward the wall. After a few trials, I realized that the robot was doing exactly what I told it to do – drive the front/back measurement error to zero, but unfortunately ‘zero’ did not equate to ‘parallel’. After scratching my head for a while, I realized that rather than using zero as the setpoint, I should use the value that causes the robot to travel parallel to the wall – which turned out to be about 0.25. Using this value I could increase the Kp value back up to 400 or so, and this resulted in very good tracking of whatever offset resulted from the ‘offset approach’ phase of the tracking algorithm. Just this step was a huge improvement in tracking performance, but it wasn’t quite ‘offset tracking’ yet as it didn’t pay any attention to the actual offset – just the difference between the front and back wall offset measurements.

Once I had this working, I was able to re-incorporate my earlier idea of biasing the actual steering value with a term that is proportional to the actual offset, i.e.

WallTrackSteerVal = glRightSteeringVal + (float)(glRightCenterCm – offsetCm) / 50.f;

This, coupled with the empirically determined steering value setpoint of 0.25 resulted in a very stable, very precise tracking performance, as shown in the short video below and the associated telemetry and Excel plots.

PID (400,0,0), SetPoint = +0.25

approach start: orient angle = 16.571, tgt_distCm = 35
At start: meas_dist = 15, corr_dist = 14, err = prev_err = -21
R/C/F dists = 13	15	15 Steerval = 0.290, OrientDeg = 16.57, err/prev_err = -21
Msec	RFront	RCtr	RRear	ODeg	ORad	c_dist	Err	P_err
11024	16	15	12	16.6	0.3	14	-21	-21
11135	18	17	14	16.6	0.3	16	-19	-21
11249	20	18	16	16.6	0.3	17	-18	-19
11365	22	22	18	16.6	0.3	21	-14	-18
11480	26	24	21	16.6	0.3	23	-12	-14
11591	29	27	23	16.6	0.3	25	-10	-12
11702	31	30	26	16.6	0.3	28	-7	-10
11814	34	32	29	16.6	0.3	30	-5	-7
11927	36	34	31	16.6	0.3	32	-3	-5
12037	41	38	35	16.6	0.3	36	1	-3
At end of offset capture - prev_res*res = -3
correct back to parallel (Right side): RF/RC/RR/Orient = 41	38	35	16.57
In SpinTurn(CW, 16.57, 30.00)

TrackRightWallOffset: Start tracking offset of 40cm with Kp/Ki/Kd = 400.00	0.00	0.00
Msec	LF	LC	LR		RF	RC	RR		F	Fvar	R	Rvar	Steer	Set	Output	LSpd	RSpd
12519	728	794	816		41	39	39		90	11753	60	11683	0.21	0.25	16	59	91
12619	728	794	816		41	39	38		90	11797	70	11628	0.31	0.25	-24	99	51
12719	728	794	816		41	40	38		87	11752	69	11576	0.39	0.25	-56	127	19
12817	728	794	816		41	40	38		87	11588	63	11529	0.37	0.25	-48	123	27
12917	728	113	816		42	40	38		80	11311	70	11482	0.40	0.25	-60	127	14
13016	728	794	816		42	40	40		75	10891	78	11436	0.20	0.25	20	55	95
13118	728	794	816		42	41	40		71	10302	84	11392	0.23	0.25	 8	67	83
13220	728	794	816		43	40	39		66	9523	79	11350	0.36	0.25	-44	119	30
13321	728	794	816		42	40	39		62	9693	84	11309	0.22	0.25	12	63	87
13416	728	794	816		42	40	39		59	9870	93	11273	0.27	0.25	-8	83	67
13519	728	794	816		40	39	40		57	10068	93	11237	-0.02	0.25	108	0	127
13618	728	794	816		40	39	38		54	10261	91	11202	0.14	0.25	44	31	119
13716	728	794	816		39	38	38		51	10455	107	11177	0.09	0.25	64	11	127
13817	728	794	816		40	37	37		45	10663	112	11156	0.20	0.25	20	54	95
13918	728	794	816		39	38	36		41	10879	109	11132	0.29	0.25	-16	91	58
14017	728	794	816		40	39	36		35	11109	115	11114	0.38	0.25	-52	127	23
In HandleAnomalousConditions with WALL_OFFSET_DIST_AHEAD error code detected
WALL_OFFSET_DIST_AHEAD case detected with tracking case Right
In SpinTurn(CCW, 90.00, 45.00)
IRHomingValTotalAvg = 199 
15351: glLeftCenterCm = 794 glRightCenterCm = 24
glLeftCenterCm > glRightCenterCm --> Calling TrackRightWallOffset()
15355: TrackRightWallOffset(), glRightFrontCm = 26

In TrackRightWallOffset with Kp/Ki/Kd = 400.00	0.00	0.00

In TrackRightWallOffset with RR/RC/RF = 24	24	26
straight window = 8 cm
R/C/F dists = 24	24	26 Steerval = 0.170, WallAngle = 9.71, Inside
In SpinTurn(CCW, 20.29, 45.00)
R/C/F dists = 26	31	32 Steerval = 0.590, WallOrientDeg = 33.71

approach start: orient angle = 33.714, tgt_distCm = 35
At start: meas_dist = 31, corr_dist = 26, err = prev_err = -9
R/C/F dists = 26	31	32 Steerval = 0.590, OrientDeg = 33.71, err/prev_err = -9
Msec	RFront	RCtr	RRear	ODeg	ORad	c_dist	Err	P_err
15712	33	31	27	33.7	0.6	25	-10	-9
15826	37	34	29	33.7	0.6	28	-7	-10
15940	38	37	32	33.7	0.6	30	-5	-7
16053	42	41	36	33.7	0.6	34	-1	-5
16165	46	44	39	33.7	0.6	36	1	-1
At end of offset capture - prev_res*res = -1
correct back to parallel (Right side): RF/RC/RR/Orient = 46	44	39	33.71
In SpinTurn(CW, 33.71, 30.00)

TrackRightWallOffset: Start tracking offset of 40cm with Kp/Ki/Kd = 400.00	0.00	0.00
Msec	LF	LC	LR		RF	RC	RR		F	Fvar	R	Rvar	Steer	Set	Output	LSpd	RSpd
16862	112	110	125		43	43	42		108	11196	64	11178	0.25	0.25	 0	75	75
16964	728	110	816		45	43	42		108	11162	65	11179	0.27	0.25	-8	82	67
17060	728	111	127		44	42	40		104	11135	61	11186	0.39	0.25	-56	127	19
17161	110	114	124		42	42	41		102	11105	70	11186	0.19	0.25	24	51	99
17263	728	114	126		44	42	41		100	11077	75	11184	0.30	0.25	-20	94	55
17362	728	115	816		43	42	41		97	11038	71	11186	0.23	0.25	 8	67	83
17461	728	116	126		43	41	41		95	10989	77	11185	0.24	0.25	 4	71	79
17562	728	113	816		44	41	41		90	10938	86	11183	0.36	0.25	-44	119	30
17664	728	109	124		43	41	41		84	10886	91	11180	0.24	0.25	 4	71	79
17763	728	118	816		41	41	41		82	10825	90	11179	0.07	0.25	72	3	127
17860	728	794	127		42	39	39		79	10762	90	11178	0.29	0.25	-16	91	59
17961	728	115	816		41	40	39		73	10708	106	11182	0.23	0.25	 8	67	83
18059	728	120	816		42	39	39		69	10656	106	11186	0.21	0.25	16	59	91
18161	728	116	816		41	39	39		64	10608	105	11189	0.15	0.25	40	35	115
18262	728	121	816		40	39	36		60	10550	113	11198	0.35	0.25	-40	115	35
18360	728	121	816		40	38	38		58	10482	124	11217	0.17	0.25	32	42	107
18459	728	121	816		40	38	37		53	10405	117	11228	0.22	0.25	12	63	87
18561	728	121	816		40	38	39		49	10600	750	19677	0.07	0.25	72	3	127
18659	728	794	816		40	39	37		43	10806	819	29443	0.24	0.25	 4	71	79
18762	728	120	816		40	39	36		36	11021	819	38752	0.37	0.25	-48	122	27
In HandleAnomalousConditions with WALL_OFFSET_DIST_AHEAD error code detected
WALL_OFFSET_DIST_AHEAD case detected with tracking case Right
In SpinTurn(CCW, 90.00, 45.00)
IRHomingValTotalAvg = 273 
19919: glLeftCenterCm = 794 glRightCenterCm = 25
glLeftCenterCm > glRightCenterCm --> Calling TrackRightWallOffset()
19923: TrackRightWallOffset(), glRightFrontCm = 28

In TrackRightWallOffset with Kp/Ki/Kd = 400.00	0.00	0.00

In TrackRightWallOffset with RR/RC/RF = 26	25	28
straight window = 8 cm
R/C/F dists = 26	25	28 Steerval = 0.180, WallAngle = 10.29, Inside
In SpinTurn(CCW, 19.71, 45.00)
R/C/F dists = 25	28	30 Steerval = 0.490, WallOrientDeg = 28.00

approach start: orient angle = 28.000, tgt_distCm = 35
At start: meas_dist = 28, corr_dist = 25, err = prev_err = -10
R/C/F dists = 25	28	30 Steerval = 0.520, OrientDeg = 29.71, err/prev_err = -10
Msec	RFront	RCtr	RRear	ODeg	ORad	c_dist	Err	P_err
20308	30	28	25	29.7	0.5	24	-11	-10
20420	32	30	26	29.7	0.5	26	-9	-11
20533	33	32	29	29.7	0.5	26	-9	-9
20647	36	33	30	29.7	0.5	28	-7	-9
20761	38	36	32	29.7	0.5	31	-4	-7
20876	41	38	36	29.7	0.5	33	-2	-4
20988	42	42	38	29.7	0.5	36	1	-2
At end of offset capture - prev_res*res = -2
correct back to parallel (Right side): RF/RC/RR/Orient = 42	42	38	29.71
In SpinTurn(CW, 29.71, 30.00)

TrackRightWallOffset: Start tracking offset of 40cm with Kp/Ki/Kd = 400.00	0.00	0.00
Msec	LF	LC	LR		RF	RC	RR		F	Fvar	R	Rvar	Steer	Set	Output	LSpd	RSpd
21657	728	794	816		45	42	41		97	10859	68	29659	0.40	0.25	-60	127	14
21758	728	794	816		46	42	43		99	10841	69	29645	0.26	0.25	-4	79	71
21856	728	794	816		44	44	45		98	10811	65	29634	0.04	0.25	84	0	127
21956	728	794	816		45	43	44		95	10782	68	29638	0.14	0.25	44	31	119
22055	728	794	816		44	41	42		91	10754	77	29623	0.21	0.25	16	59	91
22154	728	794	816		42	40	40		85	10722	73	29601	0.21	0.25	16	59	91
22258	728	123	816		42	40	41		82	10686	77	29588	0.14	0.25	44	31	119
22356	728	794	816		42	39	39		77	10648	87	29574	0.24	0.25	 4	71	79
22459	728	794	816		41	39	40		74	10604	90	29566	0.16	0.25	36	39	111
22555	728	794	816		40	38	38		70	10564	89	29551	0.19	0.25	24	51	99
22656	728	794	816		39	37	37		68	10513	93	29539	0.08	0.25	68	7	127
22758	728	794	816		40	38	37		64	10459	107	29526	0.22	0.25	12	63	87
22855	728	123	816		42	39	37		60	10395	111	29512	0.49	0.25	-96	127	0
22957	728	121	816		43	42	39		56	10314	106	29497	0.43	0.25	-72	127	3
23057	728	794	816		42	42	39		52	10491	112	29495	0.46	0.25	-84	127	0
23156	728	794	816		43	41	40		49	10673	121	29492	0.32	0.25	-28	103	46
23256	728	794	816		44	41	41		43	10870	126	29488	0.34	0.25	-36	111	39
23355	728	794	816		43	41	40		40	11071	750	37177	0.39	0.25	-56	127	18
In HandleAnomalousConditions with WALL_OFFSET_DIST_AHEAD error code detected
WALL_OFFSET_DIST_AHEAD case detected with tracking case Right
In SpinTurn(CCW, 90.00, 45.00)
IRHomingValTotalAvg = 193 
24722: glLeftCenterCm = 794 glRightCenterCm = 30
glLeftCenterCm > glRightCenterCm --> Calling TrackRightWallOffset()
24726: TrackRightWallOffset(), glRightFrontCm = 31

In TrackRightWallOffset with Kp/Ki/Kd = 400.00	0.00	0.00

In TrackRightWallOffset with RR/RC/RF = 30	30	31
straight window = 8 cm
R/C/F dists = 30	30	31 Steerval = 0.140, WallAngle = 8.00, Inside
In SpinTurn(CCW, 22.00, 45.00)
R/C/F dists = 27	29	30 Steerval = 0.300, WallOrientDeg = 17.14

approach start: orient angle = 17.143, tgt_distCm = 35
At start: meas_dist = 29, corr_dist = 28, err = prev_err = -7
R/C/F dists = 27	29	30 Steerval = 0.300, OrientDeg = 17.14, err/prev_err = -7
Msec	RFront	RCtr	RRear	ODeg	ORad	c_dist	Err	P_err
25109	31	29	27	17.1	0.3	27	-8	-7
25220	32	30	29	17.1	0.3	28	-7	-8
25331	33	31	28	17.1	0.3	29	-6	-7
25446	34	31	30	17.1	0.3	29	-6	-6
25559	35	33	31	17.1	0.3	31	-4	-6
25674	35	34	32	17.1	0.3	32	-3	-4
25787	37	35	32	17.1	0.3	33	-2	-3
25899	39	37	33	17.1	0.3	35	0	-2
At end of offset capture - prev_res*res = 0
correct back to parallel (Right side): RF/RC/RR/Orient = 39	37	33	17.14
In SpinTurn(CW, 17.14, 30.00)

TrackRightWallOffset: Start tracking offset of 40cm with Kp/Ki/Kd = 400.00	0.00	0.00
Msec	LF	LC	LR		RF	RC	RR		F	Fvar	R	Rvar	Steer	Set	Output	LSpd	RSpd
26414	111	113	816		41	39	39		99	10861	74	37154	0.21	0.25	16	59	91
26512	113	117	123		41	40	38		100	10811	70	37167	0.27	0.25	-8	83	67
26612	109	113	118		42	38	39		96	10759	70	37170	0.29	0.25	-16	91	58
26714	111	115	124		41	39	38		94	10698	80	37163	0.34	0.25	-36	111	39
26811	109	117	119		40	38	37		88	10645	88	37159	0.27	0.25	-8	83	67
26912	111	113	124		39	38	37		84	10588	84	37172	0.24	0.25	 4	71	79
27012	113	117	816		40	38	36		80	10527	87	37178	0.23	0.25	 8	67	82
27111	728	120	124		38	37	36		77	10460	98	37165	0.12	0.25	52	23	127
27212	110	116	127		37	35	35		75	10384	101	37171	0.09	0.25	64	11	127
27314	728	114	122		36	36	36		72	10304	101	37178	-0.01	0.25	104	0	127
27412	112	117	816		35	34	33		66	10218	106	37177	0.16	0.25	36	39	111
27511	112	112	816		36	34	33		64	10126	116	37174	0.26	0.25	-4	79	71
27610	728	118	127		38	36	34		62	10261	750	44549	0.28	0.25	-12	87	62
27711	728	117	125		38	38	36		60	10406	750	51599	0.24	0.25	 4	71	79
27813	728	112	126		40	37	35		57	10556	819	53316	0.38	0.25	-52	127	23
27911	113	116	816		41	38	35		53	10713	819	53316	0.54	0.25	-116	127	0
28012	728	116	128		41	40	37		46	10888	819	53316	0.36	0.25	-44	119	30
28113	113	114	119		42	40	38		41	11075	750	59737	0.40	0.25	-60	127	14
28212	104	108	120		41	39	39		36	11273	750	65748	0.26	0.25	-4	79	71

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

approach start: orient angle = 16.571, tgt_distCm = 35

At start: meas_dist = 15, corr_dist = 14, err = prev_err = -21

R/C/F dists = 13 15 15 Steerval = 0.290, OrientDeg = 16.57, err/prev_err = -21

Msec RFront RCtr RRear ODeg ORad c_dist Err P_err

11024 16 15 12 16.6 0.3 14 -21 -21

11135 18 17 14 16.6 0.3 16 -19 -21

11249 20 18 16 16.6 0.3 17 -18 -19

11365 22 22 18 16.6 0.3 21 -14 -18

11480 26 24 21 16.6 0.3 23 -12 -14

11591 29 27 23 16.6 0.3 25 -10 -12

11702 31 30 26 16.6 0.3 28 -7 -10

11814 34 32 29 16.6 0.3 30 -5 -7

11927 36 34 31 16.6 0.3 32 -3 -5

12037 41 38 35 16.6 0.3 36 1 -3

At end of offset capture - prev_res*res = -3

correct back to parallel (Right side): RF/RC/RR/Orient = 41 38 35 16.57

In SpinTurn(CW, 16.57, 30.00)

TrackRightWallOffset: Start tracking offset of 40cm with Kp/Ki/Kd = 400.00 0.00 0.00

Msec LF LC LR RF RC RR F Fvar R Rvar Steer Set Output LSpd RSpd

12519 728 794 816 41 39 39 90 11753 60 11683 0.21 0.25 16 59 91

12619 728 794 816 41 39 38 90 11797 70 11628 0.31 0.25 -24 99 51

12719 728 794 816 41 40 38 87 11752 69 11576 0.39 0.25 -56 127 19

12817 728 794 816 41 40 38 87 11588 63 11529 0.37 0.25 -48 123 27

12917 728 113 816 42 40 38 80 11311 70 11482 0.40 0.25 -60 127 14

13016 728 794 816 42 40 40 75 10891 78 11436 0.20 0.25 20 55 95

13118 728 794 816 42 41 40 71 10302 84 11392 0.23 0.25 8 67 83

13220 728 794 816 43 40 39 66 9523 79 11350 0.36 0.25 -44 119 30

13321 728 794 816 42 40 39 62 9693 84 11309 0.22 0.25 12 63 87

13416 728 794 816 42 40 39 59 9870 93 11273 0.27 0.25 -8 83 67

13519 728 794 816 40 39 40 57 10068 93 11237 -0.02 0.25 108 0 127

13618 728 794 816 40 39 38 54 10261 91 11202 0.14 0.25 44 31 119

13716 728 794 816 39 38 38 51 10455 107 11177 0.09 0.25 64 11 127

13817 728 794 816 40 37 37 45 10663 112 11156 0.20 0.25 20 54 95

13918 728 794 816 39 38 36 41 10879 109 11132 0.29 0.25 -16 91 58

14017 728 794 816 40 39 36 35 11109 115 11114 0.38 0.25 -52 127 23

In HandleAnomalousConditions with WALL_OFFSET_DIST_AHEAD error code detected

WALL_OFFSET_DIST_AHEAD case detected with tracking case Right

In SpinTurn(CCW, 90.00, 45.00)

IRHomingValTotalAvg = 199

15351: glLeftCenterCm = 794 glRightCenterCm = 24

glLeftCenterCm > glRightCenterCm --> Calling TrackRightWallOffset()

15355: TrackRightWallOffset(), glRightFrontCm = 26

In TrackRightWallOffset with Kp/Ki/Kd = 400.00 0.00 0.00

In TrackRightWallOffset with RR/RC/RF = 24 24 26

straight window = 8 cm

R/C/F dists = 24 24 26 Steerval = 0.170, WallAngle = 9.71, Inside

In SpinTurn(CCW, 20.29, 45.00)

R/C/F dists = 26 31 32 Steerval = 0.590, WallOrientDeg = 33.71

approach start: orient angle = 33.714, tgt_distCm = 35

At start: meas_dist = 31, corr_dist = 26, err = prev_err = -9

R/C/F dists = 26 31 32 Steerval = 0.590, OrientDeg = 33.71, err/prev_err = -9

Msec RFront RCtr RRear ODeg ORad c_dist Err P_err

15712 33 31 27 33.7 0.6 25 -10 -9

15826 37 34 29 33.7 0.6 28 -7 -10

15940 38 37 32 33.7 0.6 30 -5 -7

16053 42 41 36 33.7 0.6 34 -1 -5

16165 46 44 39 33.7 0.6 36 1 -1

At end of offset capture - prev_res*res = -1

correct back to parallel (Right side): RF/RC/RR/Orient = 46 44 39 33.71

In SpinTurn(CW, 33.71, 30.00)

TrackRightWallOffset: Start tracking offset of 40cm with Kp/Ki/Kd = 400.00 0.00 0.00

Msec LF LC LR RF RC RR F Fvar R Rvar Steer Set Output LSpd RSpd

16862 112 110 125 43 43 42 108 11196 64 11178 0.25 0.25 0 75 75

16964 728 110 816 45 43 42 108 11162 65 11179 0.27 0.25 -8 82 67

17060 728 111 127 44 42 40 104 11135 61 11186 0.39 0.25 -56 127 19

17161 110 114 124 42 42 41 102 11105 70 11186 0.19 0.25 24 51 99

17263 728 114 126 44 42 41 100 11077 75 11184 0.30 0.25 -20 94 55

17362 728 115 816 43 42 41 97 11038 71 11186 0.23 0.25 8 67 83

17461 728 116 126 43 41 41 95 10989 77 11185 0.24 0.25 4 71 79

17562 728 113 816 44 41 41 90 10938 86 11183 0.36 0.25 -44 119 30

17664 728 109 124 43 41 41 84 10886 91 11180 0.24 0.25 4 71 79

17763 728 118 816 41 41 41 82 10825 90 11179 0.07 0.25 72 3 127

17860 728 794 127 42 39 39 79 10762 90 11178 0.29 0.25 -16 91 59

17961 728 115 816 41 40 39 73 10708 106 11182 0.23 0.25 8 67 83

18059 728 120 816 42 39 39 69 10656 106 11186 0.21 0.25 16 59 91

18161 728 116 816 41 39 39 64 10608 105 11189 0.15 0.25 40 35 115

18262 728 121 816 40 39 36 60 10550 113 11198 0.35 0.25 -40 115 35

18360 728 121 816 40 38 38 58 10482 124 11217 0.17 0.25 32 42 107

18459 728 121 816 40 38 37 53 10405 117 11228 0.22 0.25 12 63 87

18561 728 121 816 40 38 39 49 10600 750 19677 0.07 0.25 72 3 127

18659 728 794 816 40 39 37 43 10806 819 29443 0.24 0.25 4 71 79

18762 728 120 816 40 39 36 36 11021 819 38752 0.37 0.25 -48 122 27

In HandleAnomalousConditions with WALL_OFFSET_DIST_AHEAD error code detected

WALL_OFFSET_DIST_AHEAD case detected with tracking case Right

In SpinTurn(CCW, 90.00, 45.00)

IRHomingValTotalAvg = 273

19919: glLeftCenterCm = 794 glRightCenterCm = 25

glLeftCenterCm > glRightCenterCm --> Calling TrackRightWallOffset()

19923: TrackRightWallOffset(), glRightFrontCm = 28

In TrackRightWallOffset with Kp/Ki/Kd = 400.00 0.00 0.00

In TrackRightWallOffset with RR/RC/RF = 26 25 28

straight window = 8 cm

R/C/F dists = 26 25 28 Steerval = 0.180, WallAngle = 10.29, Inside

In SpinTurn(CCW, 19.71, 45.00)

R/C/F dists = 25 28 30 Steerval = 0.490, WallOrientDeg = 28.00

approach start: orient angle = 28.000, tgt_distCm = 35

At start: meas_dist = 28, corr_dist = 25, err = prev_err = -10

R/C/F dists = 25 28 30 Steerval = 0.520, OrientDeg = 29.71, err/prev_err = -10

Msec RFront RCtr RRear ODeg ORad c_dist Err P_err

20308 30 28 25 29.7 0.5 24 -11 -10

20420 32 30 26 29.7 0.5 26 -9 -11

20533 33 32 29 29.7 0.5 26 -9 -9

20647 36 33 30 29.7 0.5 28 -7 -9

20761 38 36 32 29.7 0.5 31 -4 -7

20876 41 38 36 29.7 0.5 33 -2 -4

20988 42 42 38 29.7 0.5 36 1 -2

At end of offset capture - prev_res*res = -2

correct back to parallel (Right side): RF/RC/RR/Orient = 42 42 38 29.71

In SpinTurn(CW, 29.71, 30.00)

TrackRightWallOffset: Start tracking offset of 40cm with Kp/Ki/Kd = 400.00 0.00 0.00

Msec LF LC LR RF RC RR F Fvar R Rvar Steer Set Output LSpd RSpd

21657 728 794 816 45 42 41 97 10859 68 29659 0.40 0.25 -60 127 14

21758 728 794 816 46 42 43 99 10841 69 29645 0.26 0.25 -4 79 71

21856 728 794 816 44 44 45 98 10811 65 29634 0.04 0.25 84 0 127

21956 728 794 816 45 43 44 95 10782 68 29638 0.14 0.25 44 31 119

22055 728 794 816 44 41 42 91 10754 77 29623 0.21 0.25 16 59 91

22154 728 794 816 42 40 40 85 10722 73 29601 0.21 0.25 16 59 91

22258 728 123 816 42 40 41 82 10686 77 29588 0.14 0.25 44 31 119

22356 728 794 816 42 39 39 77 10648 87 29574 0.24 0.25 4 71 79

22459 728 794 816 41 39 40 74 10604 90 29566 0.16 0.25 36 39 111

22555 728 794 816 40 38 38 70 10564 89 29551 0.19 0.25 24 51 99

22656 728 794 816 39 37 37 68 10513 93 29539 0.08 0.25 68 7 127

22758 728 794 816 40 38 37 64 10459 107 29526 0.22 0.25 12 63 87

22855 728 123 816 42 39 37 60 10395 111 29512 0.49 0.25 -96 127 0

22957 728 121 816 43 42 39 56 10314 106 29497 0.43 0.25 -72 127 3

23057 728 794 816 42 42 39 52 10491 112 29495 0.46 0.25 -84 127 0

23156 728 794 816 43 41 40 49 10673 121 29492 0.32 0.25 -28 103 46

23256 728 794 816 44 41 41 43 10870 126 29488 0.34 0.25 -36 111 39

23355 728 794 816 43 41 40 40 11071 750 37177 0.39 0.25 -56 127 18

In HandleAnomalousConditions with WALL_OFFSET_DIST_AHEAD error code detected

WALL_OFFSET_DIST_AHEAD case detected with tracking case Right

In SpinTurn(CCW, 90.00, 45.00)

IRHomingValTotalAvg = 193

24722: glLeftCenterCm = 794 glRightCenterCm = 30

glLeftCenterCm > glRightCenterCm --> Calling TrackRightWallOffset()

24726: TrackRightWallOffset(), glRightFrontCm = 31

In TrackRightWallOffset with Kp/Ki/Kd = 400.00 0.00 0.00

In TrackRightWallOffset with RR/RC/RF = 30 30 31

straight window = 8 cm

R/C/F dists = 30 30 31 Steerval = 0.140, WallAngle = 8.00, Inside

In SpinTurn(CCW, 22.00, 45.00)

R/C/F dists = 27 29 30 Steerval = 0.300, WallOrientDeg = 17.14

approach start: orient angle = 17.143, tgt_distCm = 35

At start: meas_dist = 29, corr_dist = 28, err = prev_err = -7

R/C/F dists = 27 29 30 Steerval = 0.300, OrientDeg = 17.14, err/prev_err = -7

Msec RFront RCtr RRear ODeg ORad c_dist Err P_err

25109 31 29 27 17.1 0.3 27 -8 -7

25220 32 30 29 17.1 0.3 28 -7 -8

25331 33 31 28 17.1 0.3 29 -6 -7

25446 34 31 30 17.1 0.3 29 -6 -6

25559 35 33 31 17.1 0.3 31 -4 -6

25674 35 34 32 17.1 0.3 32 -3 -4

25787 37 35 32 17.1 0.3 33 -2 -3

25899 39 37 33 17.1 0.3 35 0 -2

At end of offset capture - prev_res*res = 0

correct back to parallel (Right side): RF/RC/RR/Orient = 39 37 33 17.14

In SpinTurn(CW, 17.14, 30.00)

TrackRightWallOffset: Start tracking offset of 40cm with Kp/Ki/Kd = 400.00 0.00 0.00

Msec LF LC LR RF RC RR F Fvar R Rvar Steer Set Output LSpd RSpd

26414 111 113 816 41 39 39 99 10861 74 37154 0.21 0.25 16 59 91

26512 113 117 123 41 40 38 100 10811 70 37167 0.27 0.25 -8 83 67

26612 109 113 118 42 38 39 96 10759 70 37170 0.29 0.25 -16 91 58

26714 111 115 124 41 39 38 94 10698 80 37163 0.34 0.25 -36 111 39

26811 109 117 119 40 38 37 88 10645 88 37159 0.27 0.25 -8 83 67

26912 111 113 124 39 38 37 84 10588 84 37172 0.24 0.25 4 71 79

27012 113 117 816 40 38 36 80 10527 87 37178 0.23 0.25 8 67 82

27111 728 120 124 38 37 36 77 10460 98 37165 0.12 0.25 52 23 127

27212 110 116 127 37 35 35 75 10384 101 37171 0.09 0.25 64 11 127

27314 728 114 122 36 36 36 72 10304 101 37178 -0.01 0.25 104 0 127

27412 112 117 816 35 34 33 66 10218 106 37177 0.16 0.25 36 39 111

27511 112 112 816 36 34 33 64 10126 116 37174 0.26 0.25 -4 79 71

27610 728 118 127 38 36 34 62 10261 750 44549 0.28 0.25 -12 87 62

27711 728 117 125 38 38 36 60 10406 750 51599 0.24 0.25 4 71 79

27813 728 112 126 40 37 35 57 10556 819 53316 0.38 0.25 -52 127 23

27911 113 116 816 41 38 35 53 10713 819 53316 0.54 0.25 -116 127 0

28012 728 116 128 41 40 37 46 10888 819 53316 0.36 0.25 -44 119 30

28113 113 114 119 42 40 38 41 11075 750 59737 0.40 0.25 -60 127 14

28212 104 108 120 41 39 39 36 11273 750 65748 0.26 0.25 -4 79 71

All four wall sections – note straight lines are due to gaps between wall sections

So now I think I finally (I’ve only been working on this for the last three years!) have a wall tracking algorithm that actually makes sense and does what it is supposed to do – track the wall at a constant offset – yay!!

After getting the right side working, I ported everything back to the left side, with some differences; for the left side approach phase, I wound up using a fudge factor of 10cm vice 5cm to get the approach to stop near the desired offset. Also, the base steering value setpoint was -0.35 instead of +0.25, and the input (WallTrackSteerVal) wound up being

  WallTrackSteerVal = glLeftSteeringVal + ((float)glLeftCenterCm - (float)offsetCm) / 25.f;

1	WallTrackSteerVal = glLeftSteeringVal + ((float)glLeftCenterCm - (float)offsetCm) / 25.f;

With these settings, Wall-E3 seemed pretty comfortable navigating around my office ‘sandbox’, as shown in the following short video:

Stay tuned,

Frank

Teensy 4.1 Replacement for Teensy 3.5?

Leave a reply

A while back, I had some problems with damaged Teensy 3.5 main controllers on Wall-E3, my autonomous wall-following robot. I eventually traced the problem back to large voltage transients that occurred when I connected/disconnected the charging probe. These transients were conducted to the Teensy 3.5 pin used to detect the probe connection status, causing the Teensy to immediately reboot, and then eventually become unusable. I solved this problem by using a non-conductive photonic charger connect/disconnect system using the supplied charge LED on the TP5100 charger coupled to a photoresistor.

Unfortunately, I ran through most of my Teensy 3.5 stock while I was figuring this out, and now this part is unavailable from PJRC or anywhere else – maybe a victim of the world-wide chip shortage? The good news though is that the Teensys 4.1, successor to the Teensy 3.5 is available, so I purchased a few to evaluate as a replacement for the T3.5 on my robot.

The Teensy 4.1 has the same form factor and pin layout as the T3.5, which means it is a drop-in replacement in most cases. However, there are some gotchas. According to the comparison sheet on Paul Stoffregen’s PJRC site, the T4.1 is 5X faster (600MHz vs 120MHz) and has more memory. However, it doesn’t have any analog output DACs (T3.5 has 2), and more importantly, the T4.1 pins are not 5V tolerant!

To start my evaluation, I loaded a simple ‘blink’ program, and as expected it worked great. Here’s the test setup, utilizing my newly-discovered OONO breakout board.

After this first test, I am convinced that the T4.1 will work nicely as a T3.5 replacement, except possibly for the 5V tolerance issue. To investigate this, I looked at my current system schematic

Wall-E3’s main controller is directly connected to two VNH5019 motor controllers, several LEDs (the Chg Stat Display module), two INA169 current sense modules, a Pulsed Light (now owned by Garmin) LIDAR system via it’s ‘Mode’ pin, the ‘HC-05 BT Module’ (now replaced by my new 5V Reg/Wixel board) via its TX/RX pins, and the battery pack via the ‘Chg Conn’ pin (this the photonic connection discussed above). It is also connected to a MPU6050 IMU, a Teensy 3.2 running the IR charging beam detector, and another Teensy 3.5 running the 7-element VL53L0X distance sensing array, all via two different I2C ports.

The I2C ports are no problem, as they are either Teensy-to-Teensy or Teensy-to-MPU6050, which has an onboard regulator to regulate 5V down to 3.3, so the data lanes are 3.3V. The LED panels is passive (doesn’t generate any signals of its own), so that’s not a problem. The Wixel RF Transceiver inside my 5V Regulator/Wixel module runs on 3.3V, so the RX/TX lines are compatible with Teensy 4.1. The ‘Irun’, ‘Itot’ and ‘BattV’ A/D inputs are all below 3.3V at their maximum values (The Irun and Itot lines max out at about 2V (2 amps through the current sensor), while BattV maxes out at about 2.4V (8.4V max battery voltage minus 6V drop through a 6V zener diode).

The ‘Mode’ line on the LIDAR could be an issue. The original Pulsed Light LIDAR was acquired by Garmin, so the original datasheets are no longer available. The Garmin datasheet says that the MODE pin output is limited to 3.3V, but I don’t know if that is the same for the original Pulsed Light model I’m using on Wall-E3. So, I hooked up my digital O’scope to the LIDAR’s MODE pin on Wall-E3 and measured it directly. As shown in the following scope grab, the output is indeed limited to 3.3V – yay!

Pulsed Light LIDAR-Lite MODE pin pulse output. Note max amplitude (Ma) = 3.308V

So, it looks like I can drop a Teensy 4.1 into Wall-E3’s system and it should do fine. I don’t really need the speed and/or memory improvements, but I do need a replacement for the now-defunct Teensy 3.5, in case I manage to kill yet another one.

21 March 2022 Update:

I took the time today to see how (or if) the Teensy 4.1 breakout module would fit on my current Wall-E3 robot. As shown below, it’s pretty big!

Based on the above photos, I don’t think this breakout board has a future on Wall-E3. Even though the module will fit, that doesn’t take into account the fact that the wiring from the module will extend horizontally from the module, rather than vertically as it does with the plain ‘Teensy + Female header’ arrangement. It was a great idea a the time, but I guess the reality is that the breakout module will be relegated to testing,

07 September 2024 Update:

I was playing with my 4WD robot and noticed the MPU6050 IMU wasn’t responding correctly, so to start the troubleshooting process I pulled the MPU6050 off the robot and connected it to a Teensy 4.1 instead of the Teensy 3.5 I have in the robot, because I had a 4.1 available and didn’t have a 3.5. This led to a couple of interesting discoveries:

I discovered it is very difficult to get a Teensy 4.1 with pins to fit into my ‘small’ plugboard. No amount of finger pressure would get the pins to fit into the correct sockets. This continued until I discovered that, way back in the day when I first got a couple of 4.1’s to try, I had soldered header pins to all the pins on the 4.1, including the five pins across the breakout board – oops! A few seconds with a side-cutter to remove these pins and I was back in business.
The default Wire1 pins on a Teensy 4.1 are different than the ones on a 3.5/3.2, and this threw me for a bit of a loop. Eventually I figured out that Wire1.begin() gets aimed at the proper default pins based on the compile target – Teensy 4.1 vs Teensy 3.5.

After making these changes, I was able to compile and run my ‘Teensy_MPU6050_DMP6_V4.ino’ Arduino sketch and verified that my MPU6050 module was working fine.

Stay tuned,

Frank

Wall-E3 Time Required for All-Sensor Update

Leave a reply

Corralling all sensor data updates into one place:

I have been struggling with how to manage sensor data updates for Wall-E3. When I originally started working with Wall-E, it had only three sensors – a left and right-side HC-04 ‘ping’ sensor and the front LIDAR distance sensor, so data updates weren’t a significant part of the algorithm. Since then the sensor population as ballooned past the double-digit mark, with seven VL53L0X side/rear distance sensors, the front LIDAR sensor, two high-side current sensors, and the MPU6050 IMU.

Back in August 2020 I decided to change from a ‘request only when needed’ to a TIMER interrupt-based sensor update paradigm. The idea was to update all sensor data X times/sec in an Interrupt Service Routine (ISR). This worked great, but caused other problems that eventually led me to abandon this approach. In addition to not knowing exactly when/where in the program the sensor data changed, it appeared this approach was incompatible with my use of the PID library for motion control. The PID library’s ‘Compute()’ function expects to be called in a loop that runs many times faster than the PID’s internal update period (100mSec by default). PID::Compute() returns without doing anything until its internal 100mSec timer expires, at which point it does one PID computation and then resets the timer. So, there was a conflict, because I wanted to call PID::Compute() each time the TIMER ISR executed (using a ‘global’ boolean flag), but PID::Compute() wants to execute only when it’s internal timer expires. I never could figure out how to make those two requirements work together. Eventually I abandoned both of them. First, I dumped the PID library and rolled my own PIDCalcs() function that computed a new output every time it was called, and I dumped the timer ISR in favor of ‘just in time’ sensor data updates.

Fast-forward to the present, and now I’m still struggling to figure out how to manage sensor data updates. As my latest ‘sand-box’ testing showed, I need to update all the distance sensors even when I’m only tracking one side, so just updating one side or the other doesn’t work. So, I created a ‘UpdateAllDistances()’ function as shown below:

void UpdateAllDistances()
{
  //Purpose: Update all 8 distance measurements

  glFrontdistval = GetFrontDistCm();
  GetRequestedVL53l0xValues(VL53L0X_ALL);
  UpdateLRDistanceArrays(glLeftCenterCm, glRightCenterCm);
}

//08/12/20 Extracted inline FRONT_DIST_ARRAY init code so can be called from anywhere
void InitFrontDistArray()
{
  //04/01/15 initialize 'stuck detection' arrays
  //06/17/20 re-wrote for better readability
  //to ensure var > STUCK_FRONT_VARIANCE_THRESHOLD for first FRONT_DIST_ARRAY_SIZE loops
  //array is initialized with sawtooth from 0 to MAX_FRONT_DISTANCE_CM

  myTeePrint.printf("InitFrontDistArray() top: prev_mean = %d, prev_var = %d\n",
    glFront_Dist_PrevMean, glFront_Dist_PrevVar);

  int newval = 0;
  int bumpval = MAX_FRONT_DISTANCE_CM / FRONT_DIST_ARRAY_SIZE;
  bool bgoingUp = true;

  for (int i = 0; i < FRONT_DIST_ARRAY_SIZE; i++)
  {
    aFrontDist[i] = newval;
    //DEBUG!!
    //myTeePrint.printf("i = %d, newval = %d, aFrontdist[%d] = %d\n", i, newval, i, aFrontDist[i]);
    //DEBUG!!
    if (bgoingUp)
    {

      if (newval < MAX_FRONT_DISTANCE_CM - bumpval) //don't want newval > MAX_FRONT_DISTANCE_CM
      {
        newval += bumpval;
      }
      else
      {
        bgoingUp = false;
      }
    }
    else
    {
      if (newval > bumpval) //don't want newval < 0
      {
        newval -= bumpval;
      }
      else
      {
        bgoingUp = true;
      }
    }
  }

  //04/19/19 init glFront_Dist_PrevMean  & glFront_Dist_PrevVar to mean/var respectively
  long sum = 0;
  for (int i = 0; i < FRONT_DIST_ARRAY_SIZE; i++)
  {
    sum += aFrontDist[i]; //adds in rest of values
  }
  glFront_Dist_PrevMean = (float)sum / (float)FRONT_DIST_ARRAY_SIZE;

  //	Step2: calc new 'brute force' variance
  float sumsquares = 0;
  for (int i = 0; i < FRONT_DIST_ARRAY_SIZE; i++)
  {
    sumsquares += (aFrontDist[i] - glFront_Dist_PrevMean) * (aFrontDist[i] - glFront_Dist_PrevMean);
  }

  glFront_Dist_PrevVar = sumsquares / FRONT_DIST_ARRAY_SIZE;
  myTeePrint.printf("%lu: aFrontDist Init: glFront_Dist_PrevMean = %3.2f, glFront_Dist_PrevVar = %3.2f\n", millis(), glFront_Dist_PrevMean, glFront_Dist_PrevVar);
  glFrontvar = glFront_Dist_PrevVar; //added 03/30/21 to prevent 'stuck' at startup

  //DEBUG!!
  //myTeePrint.printf("Initial Front Distance Array Contents\n");
  //myTeePrint.printf("Idx\tRdist\n");
  //for (size_t i = 0; i < REAR_DIST_ARRAY_SIZE; i++)
  //{
  //  myTeePrint.printf("%d\t%d\n", i, aFrontDist[i]);
  //}
  //DEBUG!!
}

void UpdateAllDistances()

{

//Purpose: Update all 8 distance measurements

glFrontdistval = GetFrontDistCm();

GetRequestedVL53l0xValues(VL53L0X_ALL);

UpdateLRDistanceArrays(glLeftCenterCm, glRightCenterCm);

}

//08/12/20 Extracted inline FRONT_DIST_ARRAY init code so can be called from anywhere

void InitFrontDistArray()

{

//04/01/15 initialize 'stuck detection' arrays

//06/17/20 re-wrote for better readability

//to ensure var > STUCK_FRONT_VARIANCE_THRESHOLD for first FRONT_DIST_ARRAY_SIZE loops

//array is initialized with sawtooth from 0 to MAX_FRONT_DISTANCE_CM

myTeePrint.printf("InitFrontDistArray() top: prev_mean = %d, prev_var = %d\n",

glFront_Dist_PrevMean, glFront_Dist_PrevVar);

int newval = 0;

int bumpval = MAX_FRONT_DISTANCE_CM / FRONT_DIST_ARRAY_SIZE;

bool bgoingUp = true;

for (int i = 0; i < FRONT_DIST_ARRAY_SIZE; i++)

{

aFrontDist[i] = newval;

//DEBUG!!

//myTeePrint.printf("i = %d, newval = %d, aFrontdist[%d] = %d\n", i, newval, i, aFrontDist[i]);

//DEBUG!!

if (bgoingUp)

{

if (newval < MAX_FRONT_DISTANCE_CM - bumpval) //don't want newval > MAX_FRONT_DISTANCE_CM

{

newval += bumpval;

}

else

{

bgoingUp = false;

}

else

{

if (newval > bumpval) //don't want newval < 0

{

newval -= bumpval;

}

else

{

bgoingUp = true;

}

//04/19/19 init glFront_Dist_PrevMean & glFront_Dist_PrevVar to mean/var respectively

long sum = 0;

for (int i = 0; i < FRONT_DIST_ARRAY_SIZE; i++)

{

sum += aFrontDist[i]; //adds in rest of values

}

glFront_Dist_PrevMean = (float)sum / (float)FRONT_DIST_ARRAY_SIZE;

// Step2: calc new 'brute force' variance

float sumsquares = 0;

for (int i = 0; i < FRONT_DIST_ARRAY_SIZE; i++)

{

sumsquares += (aFrontDist[i] - glFront_Dist_PrevMean) * (aFrontDist[i] - glFront_Dist_PrevMean);

}

glFront_Dist_PrevVar = sumsquares / FRONT_DIST_ARRAY_SIZE;

myTeePrint.printf("%lu: aFrontDist Init: glFront_Dist_PrevMean = %3.2f, glFront_Dist_PrevVar = %3.2f\n", millis(), glFront_Dist_PrevMean, glFront_Dist_PrevVar);

glFrontvar = glFront_Dist_PrevVar; //added 03/30/21 to prevent 'stuck' at startup

//DEBUG!!

//myTeePrint.printf("Initial Front Distance Array Contents\n");

//myTeePrint.printf("Idx\tRdist\n");

//for (size_t i = 0; i < REAR_DIST_ARRAY_SIZE; i++)

//{

// myTeePrint.printf("%d\t%d\n", i, aFrontDist[i]);

//}

//DEBUG!!

}

This function also causes the front and rear distance arrays to be updated and new front/rear variances to be calculated. The function is intended to be called from both the left and right wall tracking loops, and anywhere else updated distance and related data updates are required.

Having created this function, the next question becomes – how long does this function take to execute? If it is too long, then tracking performance will suffer. To answer this question, I placed code at the beginning and end of UpdateAllDistances() to toggle a hardware pin so I can measure the elapsed time on a scope, and I placed code at the beginning/end of a small WALL_TRACK_UPDATE_INTERVAL_MSEC test loop in setup(), as follows:

  //03/08/22 temporary code to measure UpdateAllEnvironmentParametes() duration
  myTeePrint.printf("Temporary duration measurement tests...\n");
  mSecSinceLastWallTrackUpdate = 0;
  uint16_t numdots = 0;
  while (true)
  {
    if (mSecSinceLastWallTrackUpdate >= WALL_TRACK_UPDATE_INTERVAL_MSEC)
    {
      mSecSinceLastWallTrackUpdate -= WALL_TRACK_UPDATE_INTERVAL_MSEC;
      digitalToggle(DURATION_MEASUREMENT_PIN2);

      myTeePrint.printf("%lu\n", millis());

      UpdateAllEnvironmentParameters();
    }
  }

//03/08/22 temporary code to measure UpdateAllEnvironmentParametes() duration

myTeePrint.printf("Temporary duration measurement tests...\n");

mSecSinceLastWallTrackUpdate = 0;

uint16_t numdots = 0;

while (true)

{

if (mSecSinceLastWallTrackUpdate >= WALL_TRACK_UPDATE_INTERVAL_MSEC)

{

mSecSinceLastWallTrackUpdate -= WALL_TRACK_UPDATE_INTERVAL_MSEC;

digitalToggle(DURATION_MEASUREMENT_PIN2);

myTeePrint.printf("%lu\n", millis());

UpdateAllEnvironmentParameters();

}

With this test, I got the following output on my HANMATECK DOS1102 digital O’Scope:

200mSec tracking loop (blue) and UpdateAllEnvironmentParameters() duration (yellow)

As can bee seen in the above plot, UpdateAllEnvironmentParameters() takes around 6-10mSec to update all environmental parameters (basically everything except MPU6050 heading), leaving 190-194mSec to complete the rest of the tracking update loop. This is very good news, as it means I can basically think of UpdateAllEnvironmentParameters() as a one-line ‘do everything’ command with negligible duration.

Next I made the same measurement, but this time with the actual ‘TrackLeftWallOffset() code being executed. As can be seen from the following image, the result is essentially identical to the first test; UpdateAllEnvironmentParameters() takes around 6-10mSec.

Then I did this test one more time, except this time I toggled the blue trace at the beginning and end of wall track processing, to show the time remaining in the 200mSec loop. Here’s what actually happens in the tracking loop:

    //09/04/21 back to elapsedMillis timing
    if (mSecSinceLastWallTrackUpdate > WALL_TRACK_UPDATE_INTERVAL_MSEC)
    {
      digitalToggle(DURATION_MEASUREMENT_PIN2); //03/08/22 toggle duration measurement pulse

      mSecSinceLastWallTrackUpdate -= WALL_TRACK_UPDATE_INTERVAL_MSEC;

      //03/08/22 abstracted these calls to UpdateAllEnvironmentParameters()
      UpdateAllEnvironmentParameters();//03/08/22 added to consolidate sensor update calls
      errcode = CheckForErrorCondx();

      //have to weight value by both angle and wall offset
      WallTrackSteerVal = glLeftSteeringVal + (glLeftCenterCm - WALL_OFFSET_TGTDIST_CM) / 1000.f;

      //update motor speeds, skipping bad values
      if (!isnan(WallTrackSteerVal))
      {

        //02/05/22 sampleTime removed from signature
        WallTrackOutput = PIDCalcs(WallTrackSteerVal, WallTrackSetPoint, lastError, lastInput, lastIval, lastDerror,
          kp, ki, kd);

        int glLeftspeednum = MOTOR_SPEED_QTR + WallTrackOutput;
        int glRightspeednum = MOTOR_SPEED_QTR - WallTrackOutput;

        glRightspeednum = (glRightspeednum <= MOTOR_SPEED_HALF) ? glRightspeednum : MOTOR_SPEED_HALF;
        glRightspeednum = (glRightspeednum > 0) ? glRightspeednum : 0;
        glLeftspeednum = (glLeftspeednum <= MOTOR_SPEED_HALF) ? glLeftspeednum : MOTOR_SPEED_HALF;
        glLeftspeednum = (glLeftspeednum > 0) ? glLeftspeednum : 0;

        MoveAhead(glLeftspeednum, glRightspeednum);

        myTeePrint.printf("%lu\t%d\t%d\t%d\t%d\t\t%d\t%d\t%d\t%d\t\t%2.2f\t%2.2f\t\t%2.2f\t%2.2f\n",
          millis(),
          glLeftFrontCm, glLeftCenterCm, glLeftRearCm, glRearCm,
          glRightFrontCm, glRightCenterCm, glRightRearCm, glFrontdistval,
          glFrontvar, glRearvar,
          WallTrackSteerVal, WallTrackSetPoint);
      }
      digitalToggle(DURATION_MEASUREMENT_PIN2); //03/08/22 toggle duration measurement pulse

    }

//09/04/21 back to elapsedMillis timing

if (mSecSinceLastWallTrackUpdate > WALL_TRACK_UPDATE_INTERVAL_MSEC)

{

digitalToggle(DURATION_MEASUREMENT_PIN2); //03/08/22 toggle duration measurement pulse

mSecSinceLastWallTrackUpdate -= WALL_TRACK_UPDATE_INTERVAL_MSEC;

//03/08/22 abstracted these calls to UpdateAllEnvironmentParameters()

UpdateAllEnvironmentParameters();//03/08/22 added to consolidate sensor update calls

errcode = CheckForErrorCondx();

//have to weight value by both angle and wall offset

WallTrackSteerVal = glLeftSteeringVal + (glLeftCenterCm - WALL_OFFSET_TGTDIST_CM) / 1000.f;

//update motor speeds, skipping bad values

if (!isnan(WallTrackSteerVal))

{

//02/05/22 sampleTime removed from signature

WallTrackOutput = PIDCalcs(WallTrackSteerVal, WallTrackSetPoint, lastError, lastInput, lastIval, lastDerror,

kp, ki, kd);

int glLeftspeednum = MOTOR_SPEED_QTR + WallTrackOutput;

int glRightspeednum = MOTOR_SPEED_QTR - WallTrackOutput;

glRightspeednum = (glRightspeednum <= MOTOR_SPEED_HALF) ? glRightspeednum : MOTOR_SPEED_HALF;

glRightspeednum = (glRightspeednum > 0) ? glRightspeednum : 0;

glLeftspeednum = (glLeftspeednum <= MOTOR_SPEED_HALF) ? glLeftspeednum : MOTOR_SPEED_HALF;

glLeftspeednum = (glLeftspeednum > 0) ? glLeftspeednum : 0;

MoveAhead(glLeftspeednum, glRightspeednum);

myTeePrint.printf("%lu\t%d\t%d\t%d\t%d\t\t%d\t%d\t%d\t%d\t\t%2.2f\t%2.2f\t\t%2.2f\t%2.2f\n",

millis(),

glLeftFrontCm, glLeftCenterCm, glLeftRearCm, glRearCm,

glRightFrontCm, glRightCenterCm, glRightRearCm, glFrontdistval,

glFrontvar, glRearvar,

WallTrackSteerVal, WallTrackSetPoint);

}

digitalToggle(DURATION_MEASUREMENT_PIN2); //03/08/22 toggle duration measurement pulse

}

And here’s the screen grab from my O’scope showing the actual duration of everything in the above loop.

tracking loop processing duration (blue) and UpdateAllEnvironmentParameters() duration (yellow)

As can be seen, almost all of the tracking processing time is spent in UpdateAllEnvironmentParameters(), and there is plenty of time to do additional processing (like anomaly handling). The 200 mSec loop is denoted above by adjacent rising edges of the blue trace, and all processing is finished at the trailing edge of the blue trace, so only about 10mSec, or about 5%, of the 200mSec is taken.

So it is clear that consolidating all environmental sensor updates into one function is a big winner. The time taken for sensor data updates is a small percentage of the time available for the entire tracking loop, but it is almost all of the time required in each tracking loop. This is very interesting result. The time required for sensor update probably cannot be reduced, as it depends on the actual hardware sensor response times and the ability to get the sensor data back to the main Teensy 3.5 processor via I2C. However, it now appears that I could easily reduce the overall tracking loop duration from the nominal 200mSec to 100, 50, or even 20mSec with no adverse effects, and presumably a corresponding increase in tracking performance. This is probably the biggest win associated with the change from the Arduino MEGA2560 to the Teensy 3.5 – so much less time required for processing.

Stay tuned,

Frank