Tag Archives: Wall-E2

Another try at Wall Offset Tracking

1 Reply

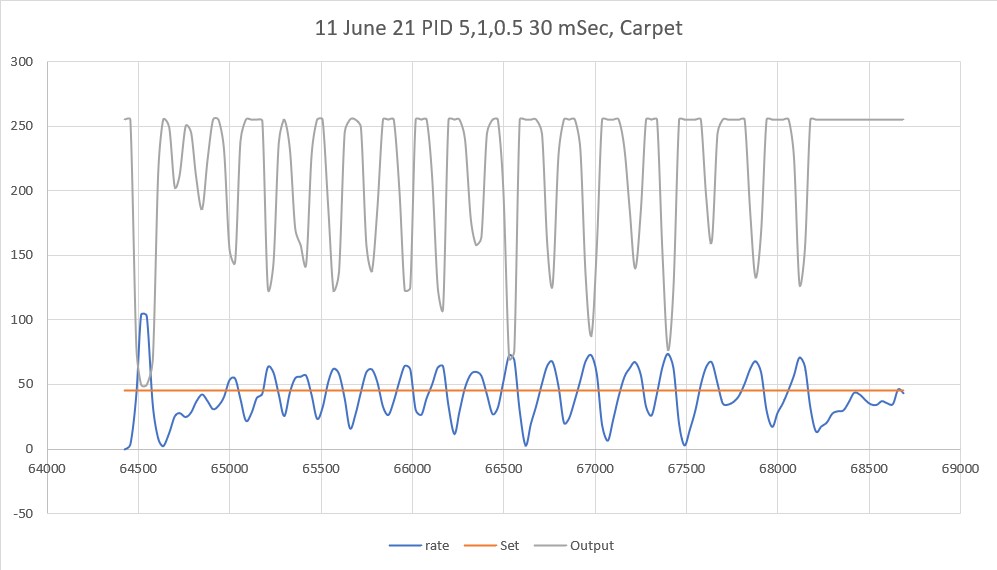
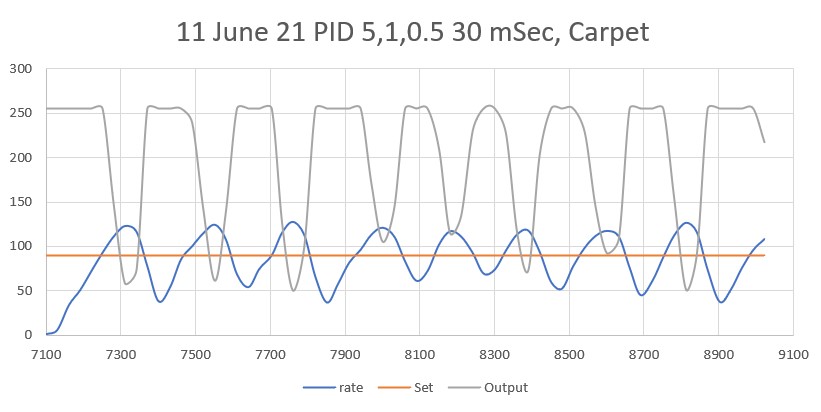
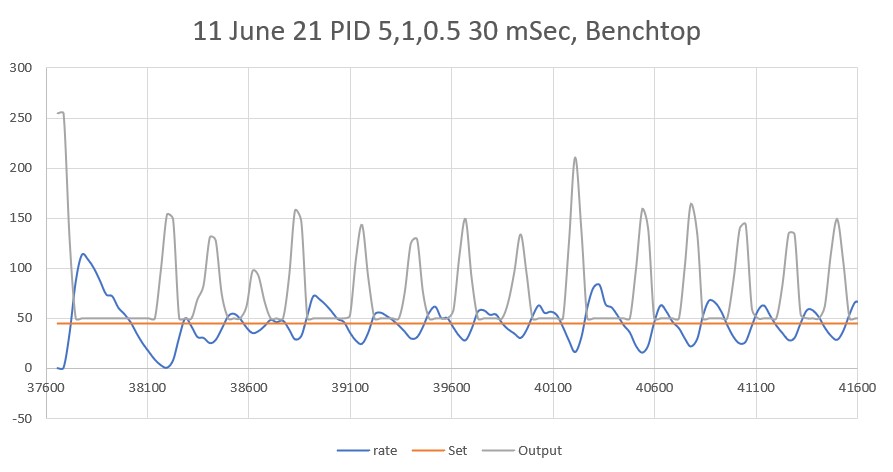
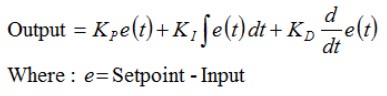Posted 11 September 2021

I’m making another try at getting wall offset capture and tracking right, after several failed attempts. This time I’m starting with a small ‘FourWD_WallTrackTest_V3’ project in VS2019. I think I actually got this working before, but an unfortunate laptop backup catastrophe cost me a couple of months of work, and it has taken me this long to recover. Here’s the current program:

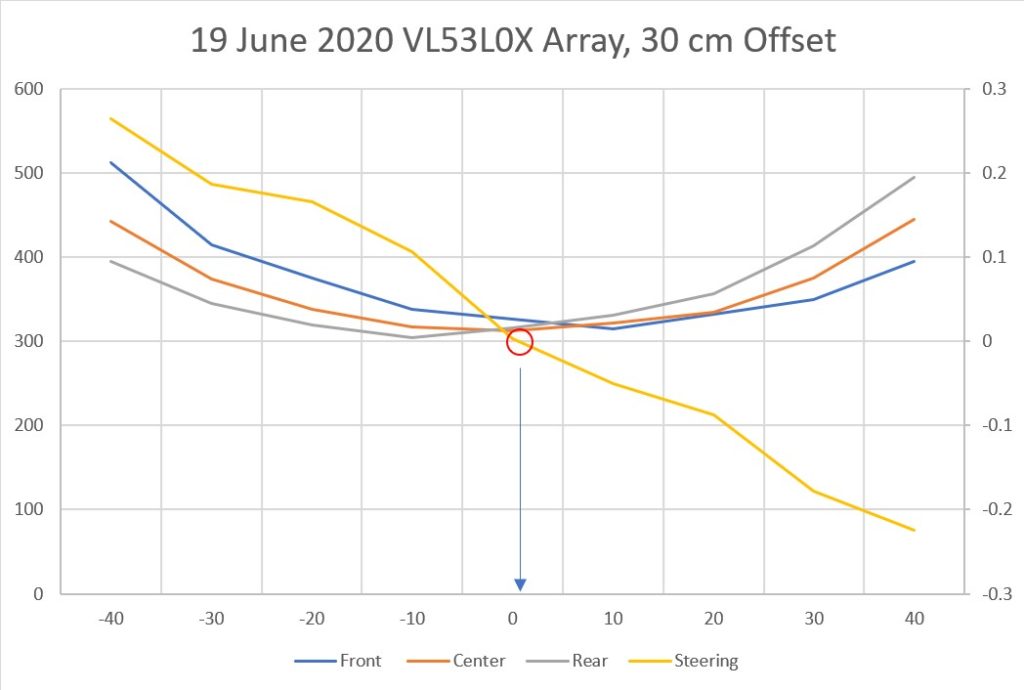
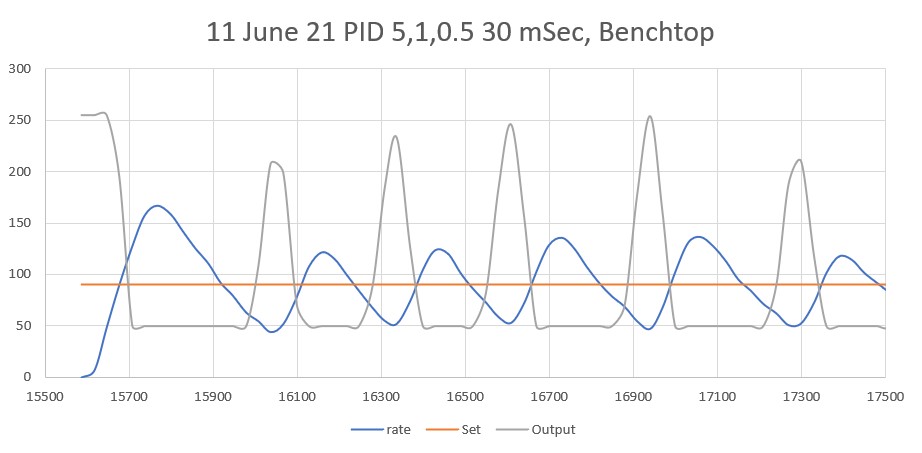
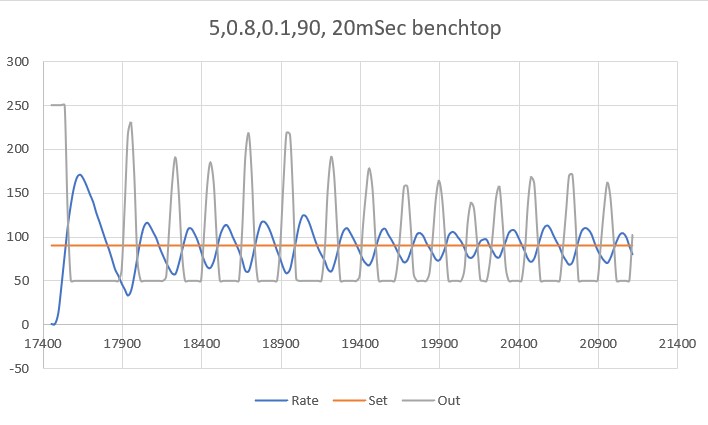
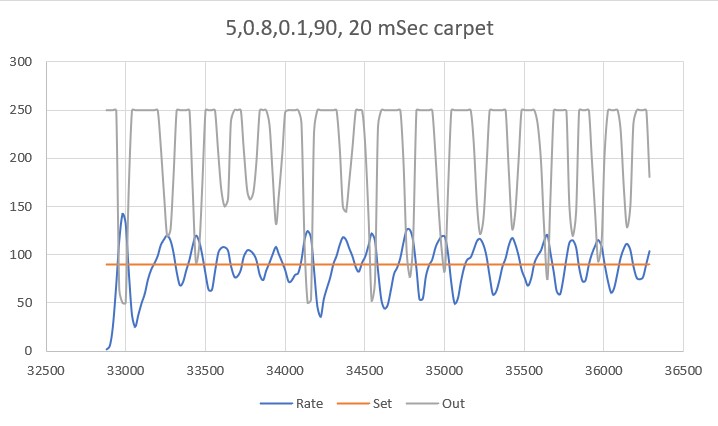
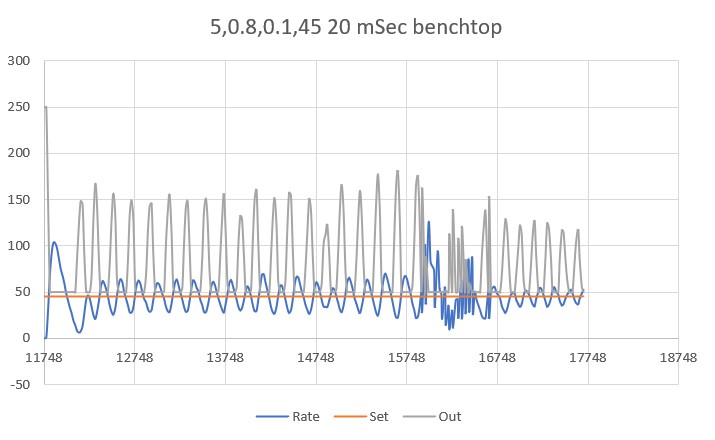
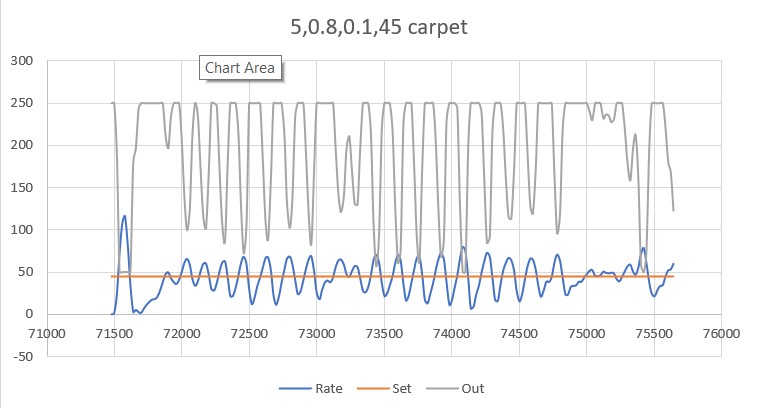
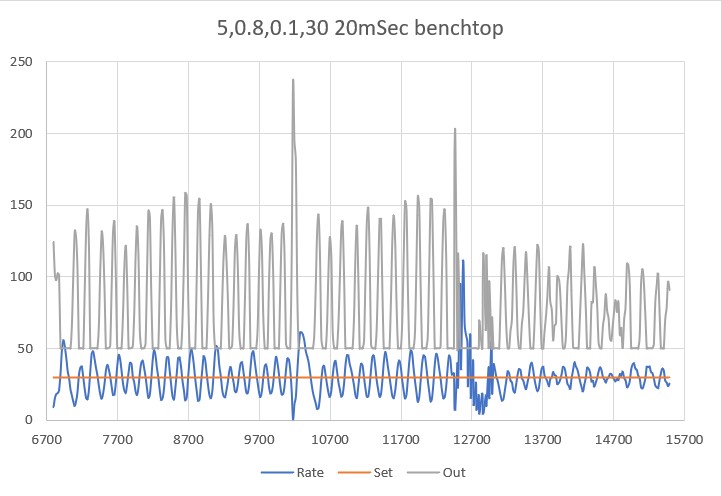
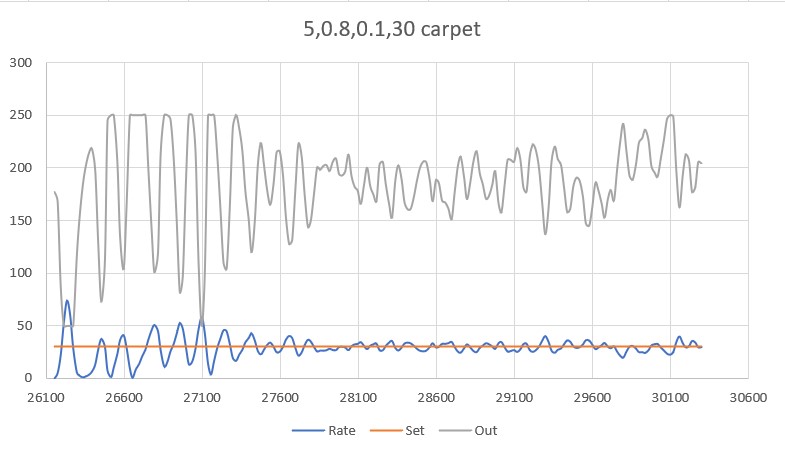
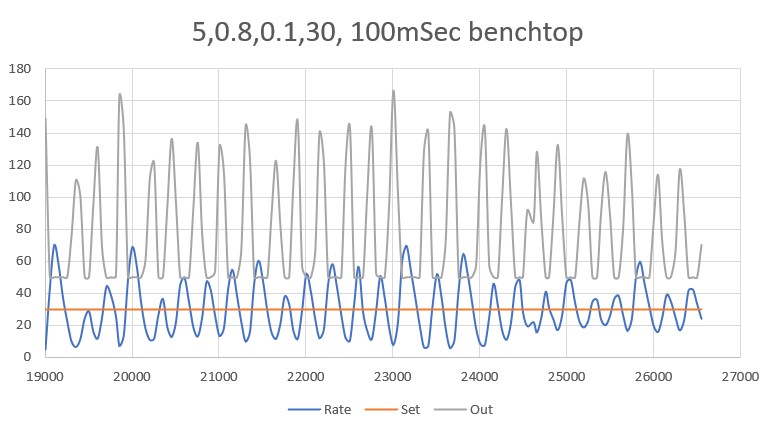
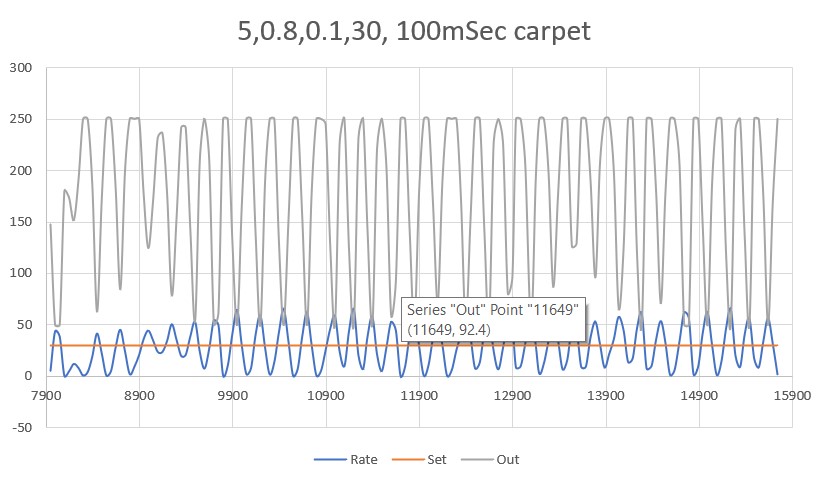
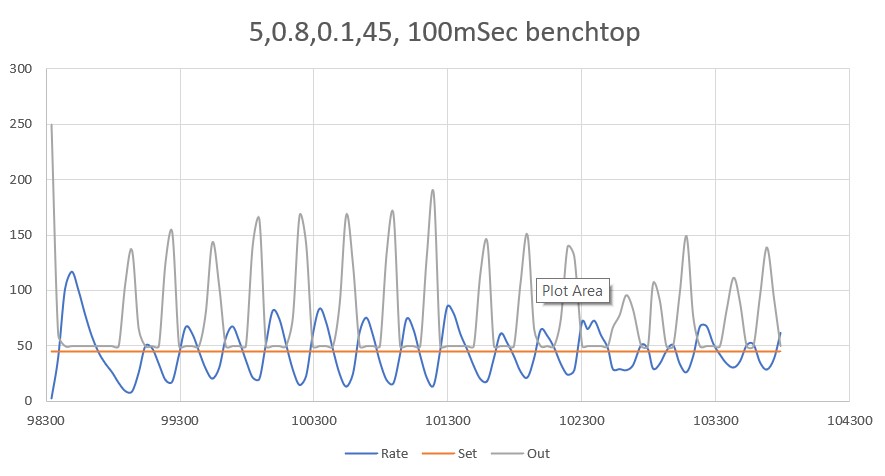
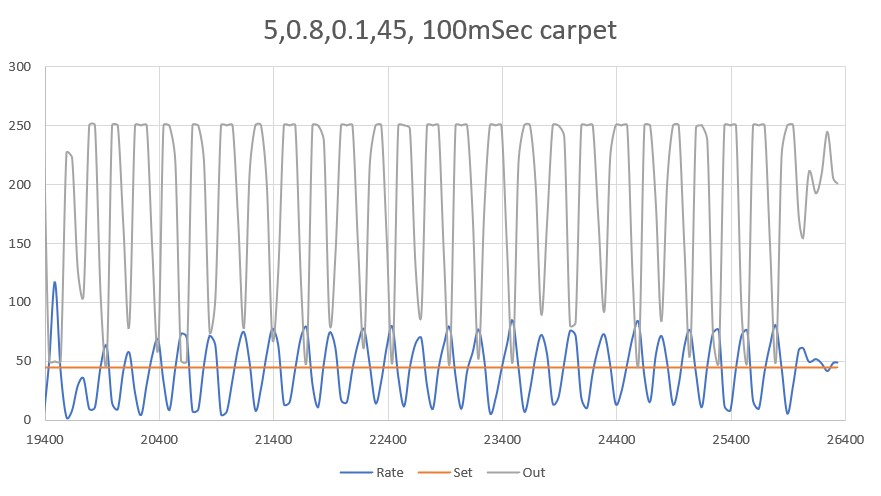
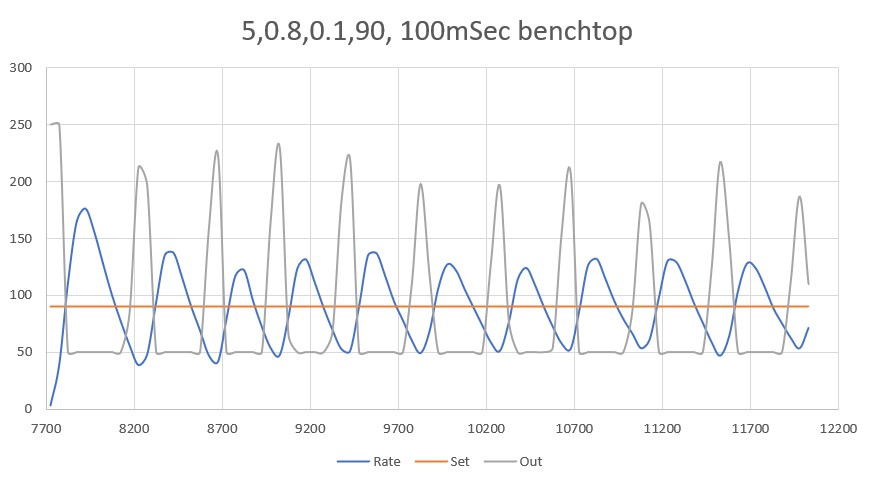
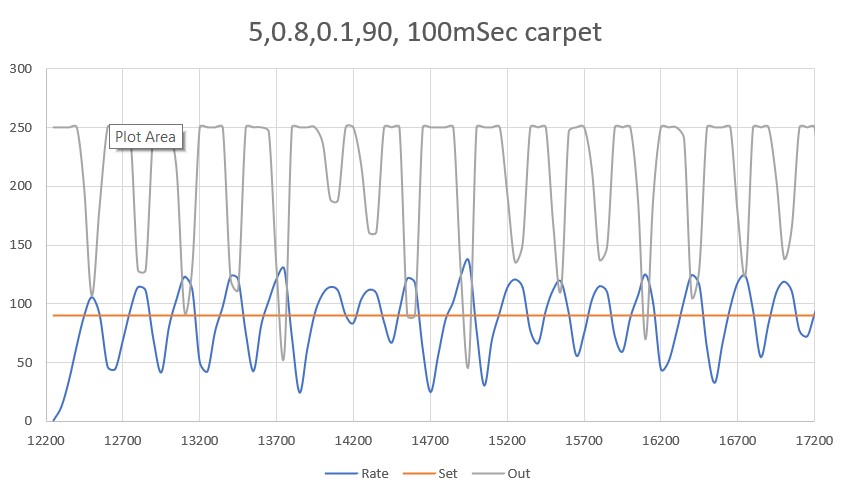
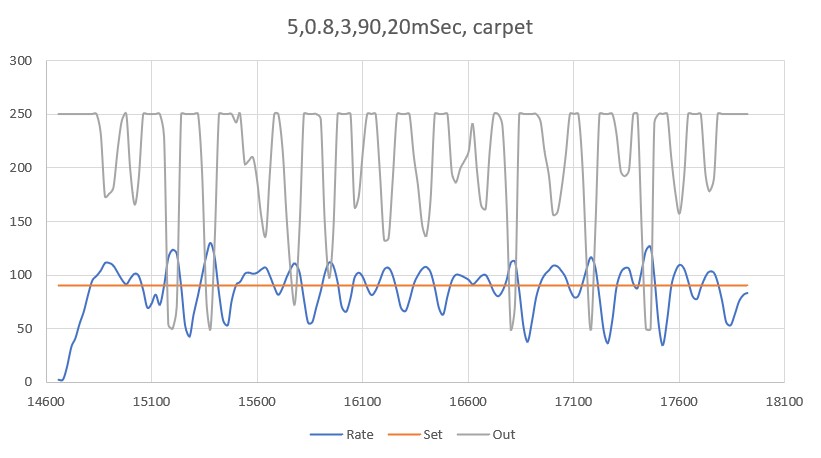
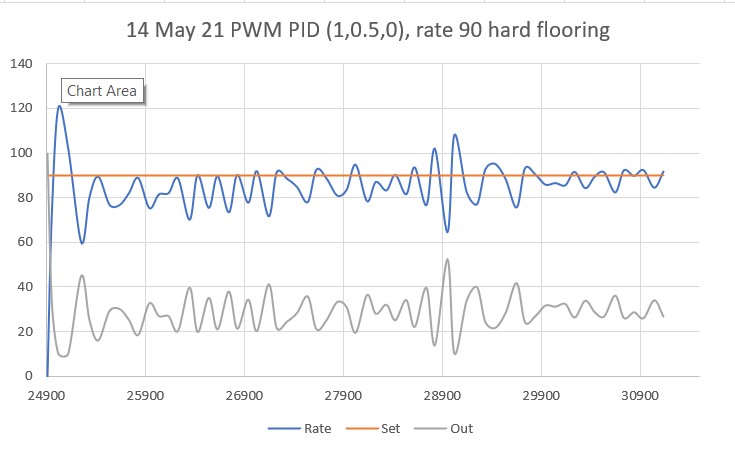
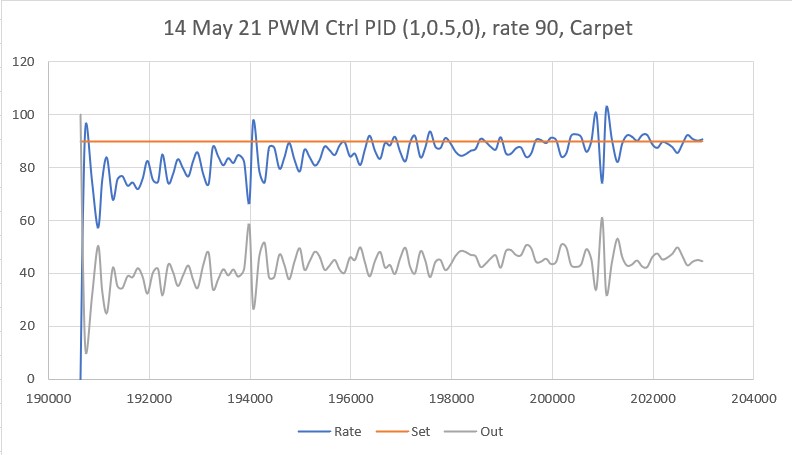
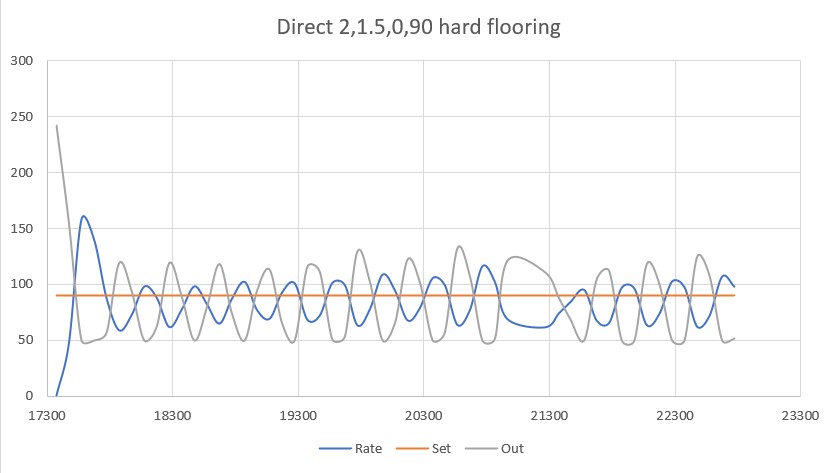
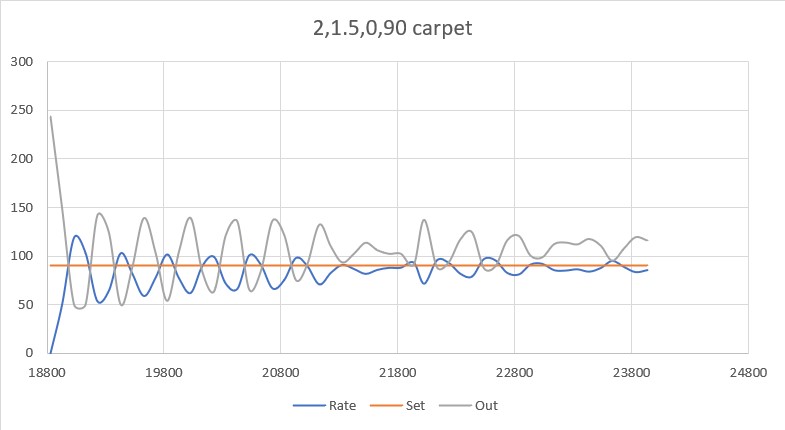
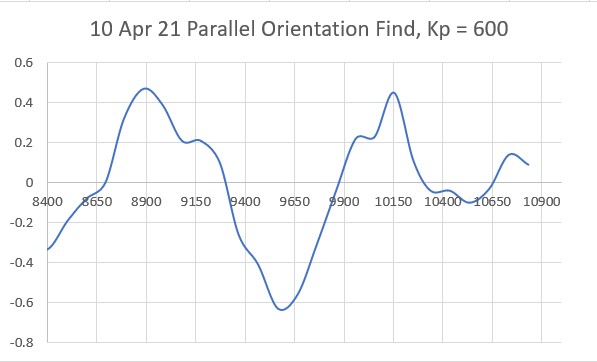
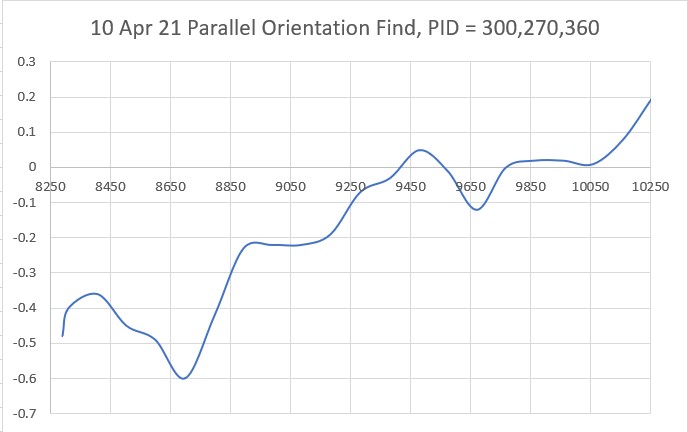
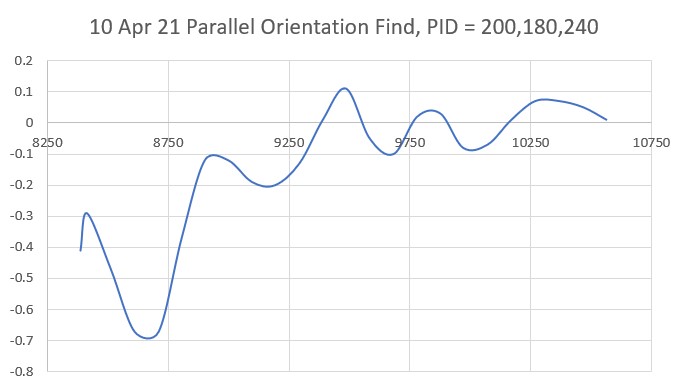
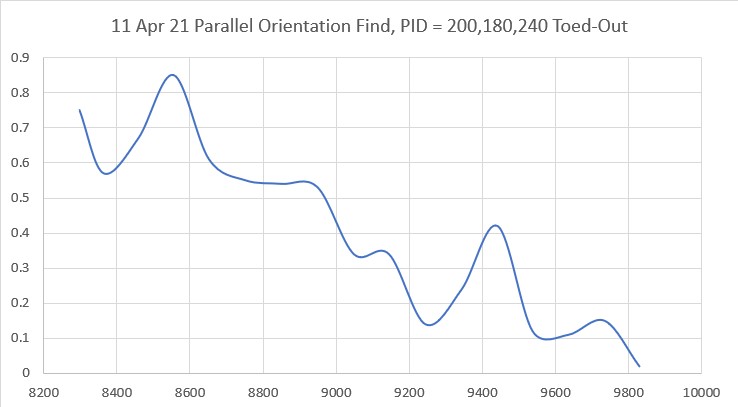
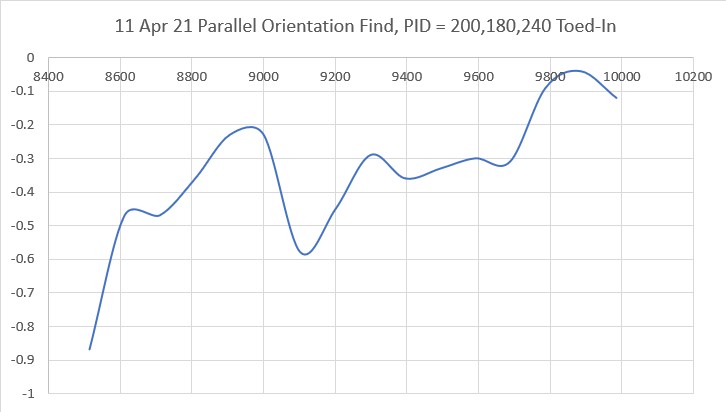
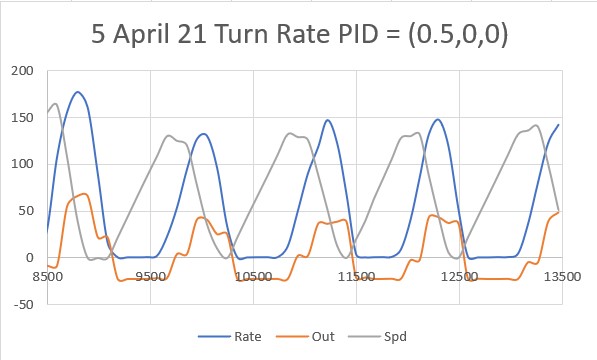
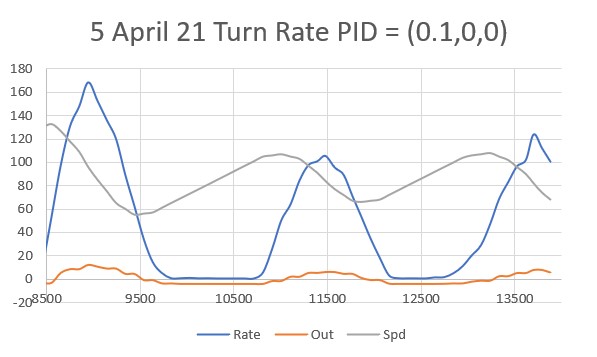
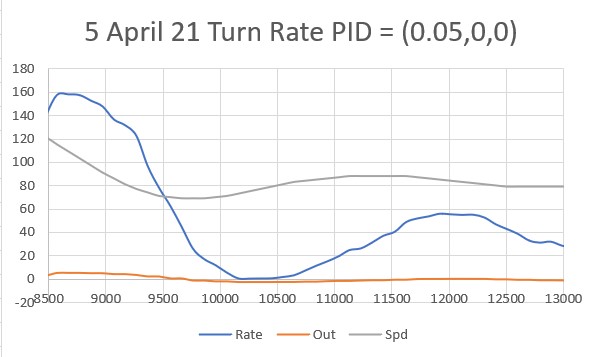
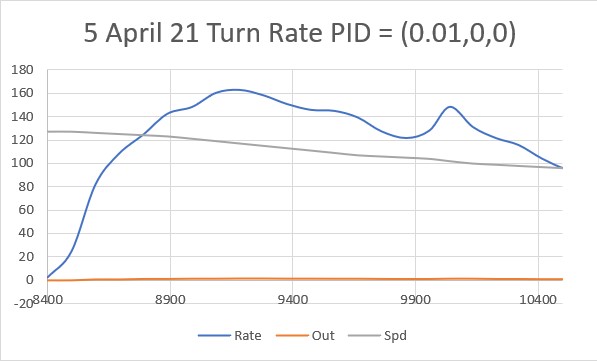
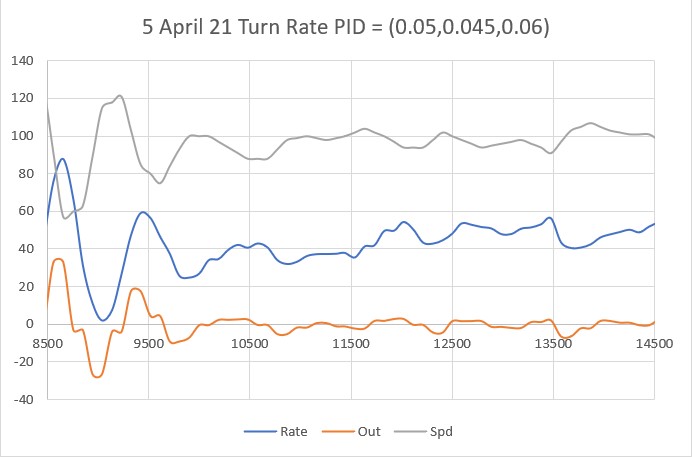
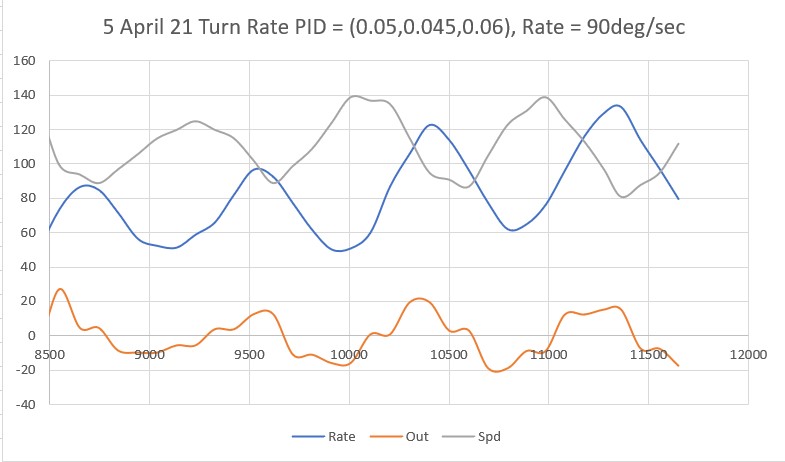
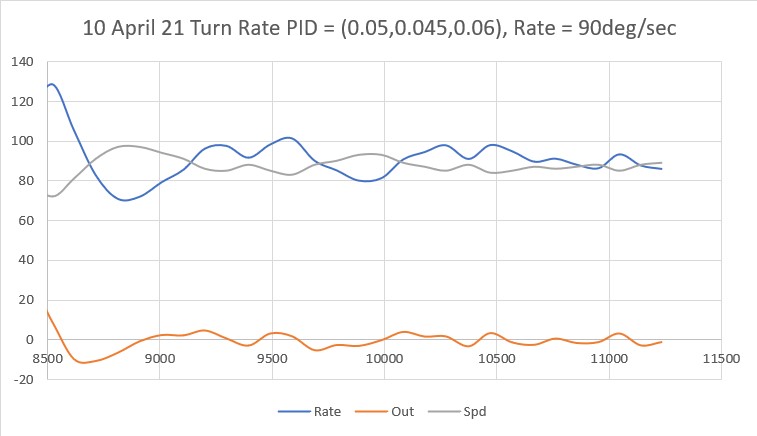
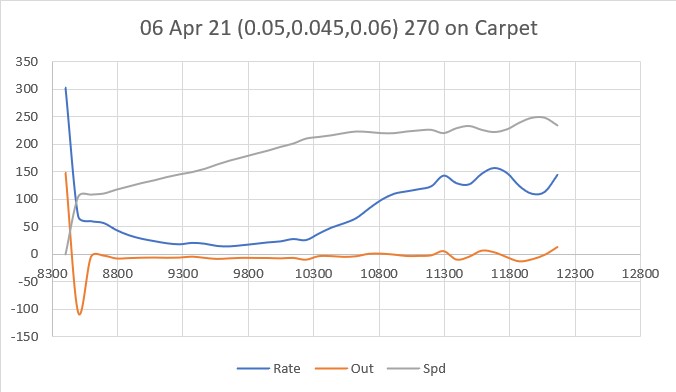
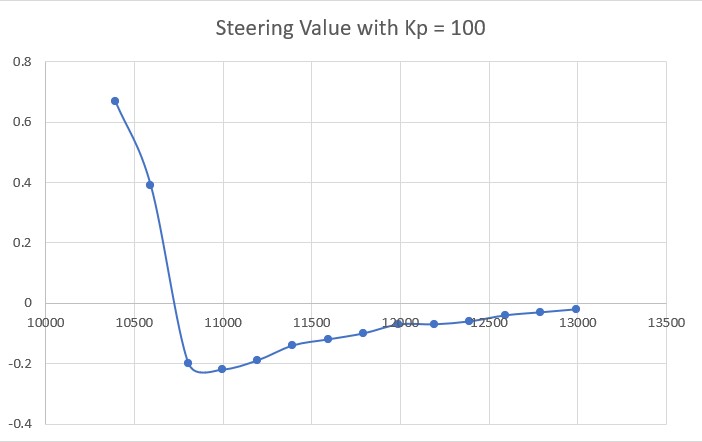
With this code, I ran a test using PID values of 300,0,0 and an offset target of 40cm. The following short video and Excel plot show the results

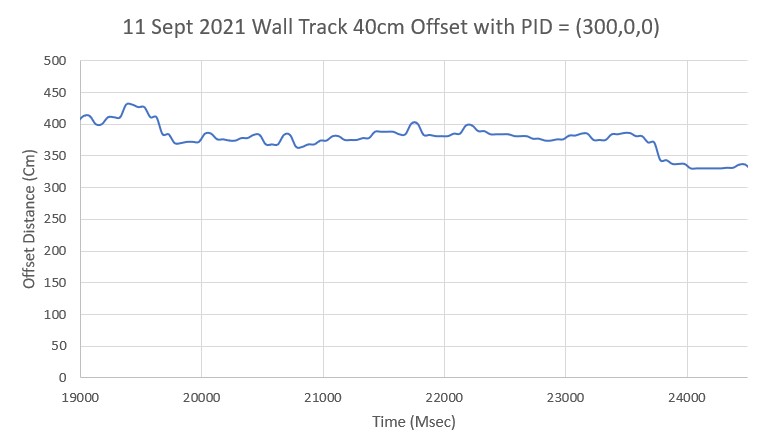
Now all I have to do is make this same trick work for both the ‘inside offset’ and ‘outside offset’ starting conditions, and then for both the left-side and right-side tracking conditions, then I can integrate the code back into the main robot operating system.

18 September 2021 Update:

After getting the left-side tracking working reasonably well, I started working on right-side tracking, and discovered that what worked for the left side with no problems did not work particularly well for right-side tracking. After the usual number of programming mistakes I did get right-side tracking working, albeit with a significantly different PID parameter set. For left-side tracking, PID = (300,0,0) seemed to work OK, but for right-side tracking I wound up with PID = (300,0,300). Moreover, when I tried even very small (like 10) values for the I parameter, the robot lost track after just two or three oscillations. So, for the moment it looks like (300,0,0) for the left side, and (300,0,300) for the right side. Here’s a short video showing successful right-side tracking.

And here is the ‘finished’ FourWD_WallTrackTest_V3 code:

Stay tuned

Frank

Another Try at Wall Offset Tracking, Part II

Leave a reply

Posted 22 June 2021

In my previous post on this subject, I described my effort to improve Wall-E2’s wall tracking performance by leveraging controlled-rate turns and the dual VL53L0X ToF LIDAR arrays. This post describes an enhancement to that effort, aimed at allowing the robot to start from a non-parallel orientation and still capture and track a desired wall offset.

The previous post showed that when starting from a parallel orientation either inside or outside the desired wall offset, the robot would make a turn toward the offset line, move straight ahead until achieving the desired offset, then turn down-track and start tracking the desired offset. The parallel starting condition was chosen to make things easier, but of course that isn’t realistic – the starting orientation may or may not be known. In previous work I created an entire function ‘RotateToParallelOrientation()’ to handle this situation, but I would rather not have to do that. It occurred to me that I might be able to eliminate this function entirely by utilizing the known characteristics of the triple-VL53L0X array. The linear array exhibits a definite relationship between ‘steering value’, (the difference between the front and rear sensor values, divided by 100) and the off-perpendicular orientation of the array. At perpendicular (parallel orientation of the robot), this value is nominally zero, and exhibits a reasonably linear relationship out to about +/- 40º from perpendicular, as shown in the following plot from this post from a year ago.

Array distances and steering value for 30 cm offset. Note steering value zero is very close to parallel orientation

As can be seen above, the ‘Steering’ value is reasonably linear, with a slope of about -0.0625/deg. So, for instance, the calculated value for an offset of 30cm would be -0.0625*30 = -0.1875, which is very close to the actual plotted value above for 30º

So, it should be possible to calculate the off-perpendicular angle of the robot, just from the measured steering value, and from that knowledge calculate the amount of rotation needed to achieve the desired offset line approach angle.

The desired approach angle was set more or less arbitrarily by

and this assumes an initial parallel orientation (i.e. 0º offset in the above plot). If, for instance, the initial steering value was -0.1875, indicating that the robot was pointing 30º away from parallel, then the code to compute the total cut (assuming we are tracking the wall on the left side of the robot) would look something like this:

So, for example, if the robot’s starting orientation was offset 30º away from the wall, and 20cm inside the desired offset line of 30cm, we would have:

cutAngleDeg = WALL_OFFSET_TGTDIST_CM – (int)(Lidar_LeftCenter / 10.f);

cutAngleDeg = 30 – 10 = 20

adjCutAngleDeg = cutAngleDeg – 30 = -10º, so the robot would actually turn 10º CCW (back toward the wall) before starting to move to capture the desired offset line.

If, on the other hand, the robot was starting from outside the desired offset (say at 60cm), but with the same (away from wall) pointing angle, then the result would be

cutAngleDeg = WALL_OFFSET_TGTDIST_CM – (int)(Lidar_LeftCenter / 10.f);

cutAngleDeg = 30 – 60 = -30

adjCutAngleDeg = cutAngleDeg – 30 = -30 – 30 = -60º, so the robot would actually turn 60º CCW (back toward the wall) before starting to move to capture the desired offset line.

26 June 2021 Update:

I modified my test program to just report the rear, center, and front VL53L0X distances, plus the steering value and the computed off-parallel angle, using the -0.0625 slope value obtained from the above plots. Unfortunately, the results were wildly unrealistic, leading me to believe something was badly wrong somewhere along the line. So, I redid the plots, thinking maybe the left side VL53L0X sensors were different enough to make that much of a difference. When I plotted the steering value vs off-parallel angle for 10, 20, 30 & 40cm wall offsets, I got a significantly different plot, as shown below:

As can be seen in the above plot, the slope of steering values to off-parallel angles is nice and linear, and also quite constant over the range of wall offset distances from 10 to 40 cm; this is quite a bit different than the behavior of the right-side sensor array, but it is what it is. In any case, it appears that the slope is close to 1.4/80 = 0.0175, or almost twice the right-side slope derived from the previous right-side plots.

Using the value of 0.0175 in my GetSteeringAngle() function results, and comparing the calculated off-parallel angle with the actual measured angle, I get the following Excel plot.

As can be seen in the above plot, the agreement between measured and calculated off-parallel angles is quite good, using the average slope value of 0.0175.

The above plot shows the raw values that produced the first plot.

So, back to my ‘FourWD_WallTrackTest’ program to develop Wall-E2’s ability to capture and then track a particular desired offset. In my first iteration, I always started with Wall-E2 parallel to the wall, and calculated an intercept angle based on the difference between the robot’s actual and desired offsets from the near wall. This worked very nicely, but didn’t address what happens if the robot doesn’t start in a parallel orientation. However, when I tried to use the data from a previous post, the results were wildly off. Now it is time to try this trick again, using the above data instead. Because the measured steering value/off angle slopes for all selected wall offsets were essentially identical, I can eliminate the intermediate step of calculating the appropriate slope value based on the current wall offset distance.

So, I modified my ‘getSteeringAngle()’ function to drop the ‘ctr_dist_mm’ parameter and to use a constant 0.0175 slope value, as shown below:

With this modification, I was able to get pretty decent results; Wall-E2 successfully captured and tracked the desired offsets from three different ‘inside’ (robot closer to wall than the desired offset) orientations, as shown in the following short videos:

‘Inside’ capture, with initial orientation angle > desired approach angle
‘Inside’ capture with initial orientation angle < desired approach angle
‘Inside’ capture with negative initial orientation angle

04 July 2021 Update:

After succeeding with the ‘inside’ cases, I started working on the ‘outside’ ones. This turned out to be considerably more difficult, as the larger distances from the wall caused considerable variation in the VL53L0X measurements (lower SNR?), which in turn produced more variation in the starting and ‘cut’ angles. However, the result does seem to be reasonably reliable, as shown in the following videos.

‘outside’ capture with initial outward angle
‘outside’ capture with initial inward angle
‘outside’ capture with small outward angle.

05 July Update:

After getting the left-side tracking algorithm working reasonably well, I ported the ‘TrackLeftWallOffset()’ functionality to ‘TrackRightWallOffset()’. After making (and mostly correcting) the usual number of mistakes, I got it going reasonably well, as shown in the following short videos:

Right wall tracking, starting inside desired offset, oriented toward wall
Right wall tracking, starting inside desired offset, oriented away from wall
Right wall tracking, starting outside desired offset, oriented toward wall
Right wall tracking, starting outside desired offset, oriented away from wall

Here is the complete code for my wall capture/track test program:

Here is a link to the above file, plus all required library & ancillary files.

Stay tuned,

Frank

Another Try at Wall Offset Tracking

1 Reply

Posted 22 June 2021

About nine months ago (October 2020) I made a run at getting offset tracking to work (see here and here). This post describes yet another attempt at getting this right, taking advantage of recent work on controlled-rate turns. I constructed a short single-task program to do just the wall tracking task, hopefully simplifying things to the point where I can understand what is happening.

One of the big issues that arose in previous work was the inability to synch my TIMER5 ISR with the PID library’s ‘Compute()’ function. The PID library insists on managing the update timing internally, which meant there was no way to ensure that Compute() would be called every time the ISR ran. I eventually came to the conclusion that I simply could not use the PID library version, and instead wrote my own small function that did the Compute() function, but with the timing value passed in as an argument rather than being managed internally. This forces the PID calculations to actually update in synch with the TIMER5 interrupt. Here’s the new PIDCalcs() function:

As can be seen from the above, this is a very simple routine that just does one thing, and doesn’t incorporate any of the improvements (windup suppression, sample time changes, etc) available in the PID library. The calling function has to manage the persistent parameters, but that’s a small price to pay for clarity and the assurance that the output value will indeed be updated every time the function is called.

With this function in hand, I worked on getting the robot to reliably track a specified offset, but was initially stymied because while I could get it to control the motors so that the robot stayed parallel to the nearest wall, I still couldn’t get it to track a specific offset. I solved this problem by leveraging my new-found ability to make accurate, rate-controlled turns; the robot first turns by an amount proportional to it’s distance from the desired offset, moves straight ahead until the offset is met, and then turns the same number of degrees in the other direction. Assuming the robot started parallel to the wall, this results in it facing the direction of travel, at the desired offset and parallel to the nearest wall. Here is the code for this algorithm.

Here are a couple of videos showing the ability to capture and track a desired offset from either side.

In both of the above videos, the desired wall offset is 30 cm.

Stay Tuned,

Frank

Turn Rate PID Tuning, Part IV

1 Reply

Posted 10 June 2021,

In my last post on this issue, I described using a small test program to explore an in-line version of the PID (Proportional-Integral-Differential) algorithm for turn rate control with Wall-E2, my autonomous wall-following robot. This post describes some follow-on work on this same subject.

The fundamental problem with all the available Arduino PID libraries is they all require the user to wait in a loop for the PID::Compute() function to decide when to actually produce a new output value, and since this computation is inside the function, it is difficult or impossible to synchronize any other related timed element with the PID function. In my case where I want to control the turn rate of a robot, the input to the PID engine is, obviously, the turn rate, in degrees/sec. But, calculation of the turn rate is necessarily a timed function, i.e. (curent_heading – last_heading) / elapsed_time, where the ‘elapsed_time’ parameter is usually a constant. But, all the Arduino PID libraries use an internal private class member that defines the measurement period (in milliseconds), and this value isn’t available externally (well, it is, but only because the user can set the sample time – it can’t be read). So, the best one can do with the current libraries is to use the same constant for PID::SetSampleTime() and for any external time-based calculations, and hope there aren’t any synchronization issues. With this setup, it would be quite possible (and inevitable IMHO) for the PID::Compute() function to skip a step, or to be ‘phase-locked’ to producing an output that is one time constant off from the input.

The solution to this problem is to not use a PID library at all, and instead place the PID algorithm in-line with the rest of the code. This ensures that the PID calculation any related time-based calculations are operating on the same schedule. The downside of this arrangement is loss of generality; all the cool enhancements described by Brett Beauregard in his wonderful PID tutorial go away or have to be implemented in-line as well. From Brett’s tutorial, here’s ‘the beginner’s PID algorithm’:

The difficulty with all the current PID libraries is the ‘dt’ parameter in the above expression; the implementation becomes much easier if ‘dt’ is a constant – i.e. the time between calculations is a constant. However, this constraint also requires that the library, not the user program, controls the timing. This just doesn’t work when the ‘Input’ parameter above also requires a constant time interval for calculation. In my case of turn rate control, the turn rate calculation requires knowledge of the time interval between calculations, and the calculation itself should be done immediately after the turn rate is determined, using the same time interval. So, the turn rate is calculated and then PID::Compute() is called, but Compute() may or may not generate a new output value, because it can return without action if it’s internal time duration criteria isn’t met; see the problem? It may, or even might, generate a new output value each time, but there is no way to ensure that it will!

After figuring this out the hard way (by trying and failing to make the library work), I finally decided to forget the library – at least for my turn rate problem, and in-line all the needed code. Once I had it all running, I abstracted just the PID algorithm to its own function so I could use it elsewhere. This function is shown below:

As you can see, the explanatory comments are much bigger than the function itself, which is really just eight lines long. Also, it has a huge number of arguments, five of which are references that are updated by the function. This function wouldn’t win any awards for good design, as it has too many arguments (wide coupling), but it does have high cohesion (does just one thing), and the coupling is at least ‘data’ coupling only.

Once this function was implemented, the calling function (in this case ‘SpinTurn()’ looks like this:

In the above code, the lines dealing with ‘TIMSK5’ are there to disable and then re-enable the TIMER5 interrupt I have set up to update external sensor values every 100 mSec. I’m not really sure that this HAS to be done, but once I learned how to do it I figured it wouldn’t hurt, either ☺

Now that I have this ‘PIDCalcs()’ function working properly, I plan to use it in several other places where I currently use the PID library; it’s just so much simpler now, and because all the relevant parameters are visible to the calling program, debugging is now a piece of cake where before it was just an opaque black box.

12 June 2021 Update:

After chasing down and eliminating a number of bugs and edge-case issues, I think I now have a pretty stable/working version of the ‘SpinTurn’ function, as shown below:

With this code in place, I made some 180º turns at 45 & 90 deg/sec, both on my benchtop and on carpet, as shown in the plots and video below:

Average turn rate = 41.8 deg/sec
Average turn rate = 86 deg/sec
Average turn rate = 44.8 deg/sec
Average turn rate = 90.1 deg/sec

Stay Tuned!

Frank

Turn Rate PID Tuning, Part III

1 Reply

In my previous post on this subject, I described my efforts to control the turn rate (in deg/sec) of my two-wheel robot, in preparation for doing the same thing on Wall-E2, four wheel drive autonomous wall following robot.

As noted previously, I have a TIMER5 Interrupt Service Routine (ISR) set up on my four wheel robot to provide updates to the various sensor values every 100 mSec, but was unable to figure out a robust way of synchronizing the PID library’s Compute() timing with the ISR timing. So, I decided to bag the PID library entirely, at least for turn rate control, and insert the PID algorithm directly into the turn rate control, and removing the extraneous stuff that caused divide-by-zero errors when the setSampleTime() function was modified to accept a zero value.

To facilitate more rapid test cycles, I created a new program that contained just enough code to initialize and read the MP6050 IMU module, and a routine called ‘SpinTurnForever() that accepts PID parameters and causes the robot to ‘spin’ turn forever (or at least until I stop it with a keyboard command. Here’s the entire program.

This program includes a function called ‘CheckForUserInput()’ that, curiously enough, monitors the serial port for user input, and uses a ‘switch’ statement to execute different commands. One of these commands (‘q’ or ‘Q’) causes ‘SpinTurnForever()’ to execute, which in turn accepts a 4-paremeter input that specifies the three PID parameters plus the desired turn rage, in deg/sec. This routine then starts and manages a CCW turn ‘forever’, in the ‘while()’ block shown below:

This routine mimics the PID library computations without suffering from library’s synchronization problems, and also allows me to fully instrument the contribution of each PID term to the output. This program also allows me to vary the computational interval independently of the rest of the program, bounded only by the ability of the MPU6050 to produce reliable readings.

After a number of trials, I started getting some reasonable results on my benchtop (hard surface with a thin electrostatic mat), as shown below:

Average turn rate = 89.6 deg/sec

As can be seen in the above plot, the turn rate is controlled pretty well around the 90 deg/sec turn rate, with an average turn rate of 89.6 deg/sec.

The plot below shows the same parameter set, but run on carpet rather than my bench.

Average turn rate = 88.2 deg/sec

Comparing these two plots it is obvious that a lot more motor current is required to make the robot turn on carpet, due to the much higher sideways friction on the wheels.

The next step was to see if the PID parameters for 90 deg/sec would also handle different turn rates. Here are the plots for 45 deg/sec on my benchtop and on carpet:

Average turn rate = 44.7 deg/sec
Average turn rate = 43.8 deg/sec

And then 30 deg/sec on benchtop and carpet

Average turn rate = 29.8 deg/sec
Average turn rate 28.8 deg/sec

It is clear from the above plots that the PID values (5,0.8,0.1) do fairly well for the four wheel robot, both on hard surfaces and carpet.

Having this kind of control over turn rate is pretty nice. I might even be able to do turns by setting the turn rate appropriately and just timing the turn, or even vary the turn rate during the turn. For a long turn (say 180 deg) I could do the first 90-120 at 90 deg/sec, and then do the last 90-60 at 30 deg/sec; might make for a much more precise turn.

All of the above tests were done with a 20 mSec time interval, which is 5x smaller than the current 100mSec time interval used for the master timer in Wall-E2. So, my next set of tests will keep the turn rate constant and slowly increase the time interval to see if I can get back to 100 mSec without any major sacrifice in performance.

28 May 2021 Update:

I went back through the tests using a 100 mSec interval instead of 20 mSec, and was gratified to see that there was very little degradation in performance. The turn performance was a bit more ‘jerky’ than with a 20 mSec interval, but still quite acceptable, and very well controlled, both on the benchtop and carpet surfaces – Yay! Here are some plots to show the performance.

Average turn rate = 29.7 deg/sec
Average turn rate = 28.4 deg/sec
Average turn rate = 44.4 deg/sec
Average turn rate = 43.0 deg/sec
Average turn rate = 89.7 deg/sec
Average turn rate = 86.6 deg/sec

31 May 2021 Update:

I made some additional runs on benchtop and carpet, thinking I might be able to reduce the turn-rate oscillations a bit. I found that by reducing the time interval back to 20 mSec and increase the ‘D’ (differential) parameter. After some tweaking back and forth, I wound up with a PID set of (5, 0.8, 3). Using these parameters, I got the following performance plots.

Average turn rate = 87.3 deg/sec
PID = (5,0.8,3), 20mSec interval, 90 deg/sec

As can be seen in the Excel plot and the movie, the turn performance is much smoother – yay!

Stay tuned!

Frank

New Batteries for Wall-E2

Leave a reply

I have been using a set of four Panasonic 18650 LiPo batteries in a 2-cell stack configuration in Wall-E2, my autonomous wall following robot. for a little over three years now, and they are starting to show their age. So, I decided to replace these

with these

Panasonic 18650G-A 3500 mAH 3.7V LiPo battery

Three years younger, and with another 100 mAH (rated, at least).

Here’s a photo record of the process of changing out the batteries

Old batteries still installed (can tell by the green showing through the ‘V5’ cutout)
Old batteries before replacement
  • Battery connection details
  • Replacement battery connection details
New batteries installed in holder

Stay tuned,

Frank

Turn Rate PID Tuning, Part II

1 Reply

Posted 14 May 2021,

In my previous post on this topic, I described my efforts to use the Arduino PID library to manage turns with Wall-E2, my autonomous wall following robot. This post talks about a problem I encountered with the PID library when used in a system that uses an external timing source, like the TIMER5 ISR in my system and a PID input that depends on accurate timing, such as my turn-rate input.

In my autonomous wall-following robot project, I use TIMER5 on the Arduino Mega 2560 to generate an interrupt ever 100 mSec, and update all time-sensitive parameters in the ISR. These include results from all seven VL53L0X ToF distance sensors, the front-mounted LIDAR, and heading information from a MP6050 IMU. This simplifies the software immensely, as now the latest information is available throughout the code, and encapsulates all sensor-related calls to a single routine.

In my initial efforts at turn-rate tuning using the Arduino PID library, I computed the turn rate in the ISR by simply using

This actually worked because, the ISR frequency and the PID::Compute() frequency were more or less the same. However, since the two time intervals are independent of each other there could be a phase shift, which might drift slowly over time. Also, if either timer interval is changed sometime down the road, the system behavior could change dramatically. I thought I had figured out how to handle this issue by moving the turn-rate computation inside the PID::Compute() function block, as shown below

In a typical PID use case, you see code like the following:

After making the above change, I started getting really weird behavior, and all my efforts at PID tuning failed miserably. After a LOT of troubleshooting and head-scratching, I finally figured out what was happening. In the above code configuration, the PID generates a new output value BEFORE the new turn rate is computed, so the PID is always operating on information that is at least 100mSec old – not a good way to run a railroad!

Some of the PID documentation I researched said (or at least implied) that by setting the PID’s sample time to zero using PID::SetSampleTime(0), that Compute() would actually produce a new output value every time it was called. This meant that I could do something like the following:

Great idea, but it didn’t work! After some more troubleshooting and head-scratching, I finally realized that the PID::SetSampleTime() function specifically disallows a value of zero, as it would cause the ‘D’ term to go to infinity – oops! Here’s the relevant code

As can be seen from the above, an argument of zero is simply ignored, and the sample time remains unchanged. When I pointed this out to the developer, he said this was by design, as the ‘ratio’ calculation above would be undefined for an input argument of zero. This is certainly a valid point, but makes it impossible to synch the PID to an external master clock – bummer!

After some more thought, I modified my copy of PID.cpp as follows:

By moving the SampleTime = (unsigned long)NewSampleTime; line out of the ‘if’ block, I can now set the sample time to zero without causing problems with the value of ‘ratio’. Now PID::Compute() will generate a new output value every time it is called, which synchs the PID engine with the program’s master timing source – yay!

I tried out a slightly modified version of this technique on my small 2-wheel robot. The two-wheeler uses an Arduino Uno instead of a Mega, so I didn’t use a TIMER interrupt. Instead I used the ‘elapsedMillisecond’ library and set up an elapsed time of 100 mSec, and also modified the program to turn indefinitely at the desired turn rate in deg/sec.

I experimented with two different methods for controlling the turn rate – a ‘PWM’ method where the wheel motors are pulsed at full speed for a variable pulse width, and a ‘direct’ method where the wheel motor speeds are varied directly to achieve the desired turn rate. I thought the PWM method might work better on a heavier robot for smaller angle turns as there is quite a bit of inertia to overcome, but the ‘direct’ method might be more accurate.

Here’s the code for the ‘direct’ method, where the wheel speeds are varied with

Here’s the code for the PWM method: the only difference is that is the duration of the pulse that is varied, not the wheel speed.

Here’s a short video showing the two-wheel robot doing a spin turn using the PWM technique with a desired turn rate of 90 deg/sec, using PID = (1,0.5,0).

The average turn rate for the entire run was about 85 deg/sec.

Here’s another run, this time on carpet:

Average turn rate for the entire run was about 85 deg/sec

Here’s some data from the ‘direct’ method, on hard flooring

Average turn rate was ~ 85 deg/sec

And on carpet

Average turn rate ~83 deg/sec

So, it appears that either the PWM or ‘direct’ methods are effective in controlling the turn rate, and I don’t really see any huge difference between them. I guess the PWM method might be a little more effective with the 4-wheel robot caused by the wheels having to slide sideways while turning.

Stay Tuned!

Frank

Wall Parallel Find PID Tuning

1 Reply

Posted 10 April 2021

In addition to using PID for homing to its charging station and for turn rate control, Wall-E2 also uses PID for finding the parallel orientation to a nearby wall. After successfully tuning the turn rate and IR Homing PID controllers using the Ziegler-Nichols method for PID tuning, I decided to see what I could do with the PID controller for parallel orientation finding

Wall-E2 uses two 3-element VL53L0X Time-of-Flight distance sensors for parallel orientation finding. The idea is that when all three sensors report the same distance, then the robot must be oriented parallel to the wall. The Teensy 3.5 Array Controller MCU calculates a ‘steering value’ using the expression (shown for the left side array):

This value is fed to the PID engine, which drives the motors to zero it out – thus arriving at a parallel orientation. Originally I just basically ‘winged it’ in choosing PID Kp, Ki & Kd values, arriving emperically at Kp = 200, Ki = 50, Kd = 0. However, after going through the K-N process with Wall-E2’s other two PID control setups, I decided to try it with this one as well.

The first step is to determine Kc, the Kp value for which the system oscillates in a reasonably stable fashion. To accomplish this I started with Kp = 20 and worked my way up in stages, plotting the ‘steering value’ each time. The last three trials (as shown in the following plots) were for Kp = 400, Kp = 500 and Kp = 600:

Looking at the above plots, it looks like Kp = 600 will work for Kc. Using the K-N formula, we get

Using the above values for the Parallel Find PID, we get the following plot:

Which is not exactly what I thought it would be – it looks like my guess for Kc must be off. Trying again with a Kc = 400 –> PID = 200,180,240, we get:

which, to my eye at least, seems a bit better.

To test how this worked with ‘real’ parallel finding, I incorporated these parameter values into my ‘RotateToParallelOrientation()’ routine and ran a couple of tests. Here’s one where Wall-E2 starts in the ‘toed-out’ position:

And here’s the Excel plot from this same run

As can be seen, the robot takes less than two seconds to converge on a pretty decent parallel orientation, starting from a 30-40º angle to the near wall.

Here’s another run where the robot starts in the ‘toed-in’ orientation.

And here’s the Excel plot for the run

Again, the robot gets to a pretty decent parallel orientation within 2 seconds of the start of the run. The only concern I have with this run is that it winds up pretty close to the wall.

Turn Rate PID Tuning

1 Reply

Posted 05 April 2021

Wall-E2, my autonomous wall-following robot, does a lot of turns to follow walls. Originally Wall-E2 used a simple timing algorithm to make turns, but this wasn’t very accurate. On a hard surface a 5-second turn at half motor speed could result in a 360º turn, while the same 5 seconds on carpet my only cover 90º. After installing the MPU6050 IMU about 18 months ago, turns could be controlled much more accurately, but the turn rate still varied widely on carpet vs hard flooring. Some time ago, I revised Wall-E2’s program to use a PID engine for turn rate control, but this resulted in a low-frequency ‘motorboating’ movement as the robot ramped up motor current until the angle started changing, followed by ramping the motor current down again because the turn rate target had been exceeded.

After having some success with improving the robot’s performance in homing to the charging station by utilizing the Zeigler-Nichols tuning method, I decided to try using it to improve turn rate control.

The method starts with setting the PID variables to (Kp, 0, 0) and then varying the Kp values to determine Kc, the value at which the setpoint variable (in this case, the turn rate in deg/sec) exhibits a steady oscillation. The value of Kc is then used to calculate all three PID parameters using

The existing setting for Kp, Ki, and Kd was Kp = 5, Ki = 0, Kd = 10, and this resulted in the following plot for a single 270º turn.

To start the process of determining Kc, I first zeroed out the Kd factor, resulting in the following plot:

So the system is clearly exhibiting a ‘constant amplitude oscillation’, but Kc is the minimum Kp value that produces oscillation. So, I started reducing Kp looking for the point at which the oscillation stopped, producing the following plots:

Comparing the above plots, it seems the value of Kc is probably around 0.1. Using the Z-N formula above, I get

These values are almost two orders of magnitude smaller than the values I had been using – ouch! Looking back on the original work, I had declared the Kp, Ki, & Kd variables as ‘const int’, which means the lowest positive value I could use was ‘1’, which might explain why I never tried anything smaller. Of course, I could have also done what I did with the home-to-charger PID engine and arranged the turn rate calculation so that instead of Kc = 0.1, it would have been more like 100, resulting in (Kp,Ki,Kd) values of (50,45,60).

Anyway, using values of (0.05, 0.045, 0.06) results in the following plot

And here is a short video showing the robot executing the 270º turn plotted above

I was quite impressed by the difference between what I had before and the current performance after implementing the Z-N tuning method; the turn rate was an almost constant 40º/sec (an average of 42.9º according to Excel). And, now that I have a semi-constant rate to look at, it appears to me that I should probably crank up the turn rate to something more like 90º/sec.

With the turn rate cranked up to 90º/sec and using the same values for Kp, Ki, Kd, I get the following plot and video.

The plot of turn rate vs time shows considerably more variation with a 90º/sec turn rate, as compared to 45º/sec; maybe Kc is different due to the different physical dynamics of the robot? The average turn rate from the Excel data is 80º/sec; not the 90º/sec I was looking for, but still not bad. Even so, this result is much better than I had before, with extreme motorboating between 0º/sec and something much higher. I may or may not try to re-determine Kc, but in the meantime I think I’ll run with this for a while.

10 April 2021 Update:

Some of the above data were collected at a pretty low charge level. When I had the opportunity to recharge Wall-E2 I re-took the 90º/sec run with the following results:

As the above plot shows, the turn rate was held almost constant (average of 87.9º) throughout the turn – very nice!

Here’s another run, this time on carpet with a fully charged battery. As expected, the robot has a harder time getting started on carpet due to the added sideways friction on the wheels. However, once the turn gets started, it stabilizes fairly well on the 90º turn rate target

Stay tuned,

Frank

Another Try at Charging Station Homing PID Tuning

Leave a reply

Posted 04 April 2021

Lately I have been working on improving the performance of Wall-E2, my autonomous wall-following robot, when homing in and connecting to it’s charging station. The robot uses the PID (Proportional-Integral-Derivative) library to drive the motors to home in on an IR beacon, and this ‘mostly’ works, but still occasionally hangs up on the lead-in rails. I have made several attempts to get this right (see this post and earlier work), but have never really gotten it zeroed in. After yet another web search for tuning help, I ran across this post dealing with the Ziegler-Nichols method for PID tuning. Basically the method starts by setting the proportional (Kp), integral (Ki) and derivative (Kd) terms to zero, and then slowly increasing the proportional (Kp) term until a ‘stable oscillation condition’ is achieved (Kp = Kc). Then the Ki & Kd terms can be calculated using the following relationships:

Getting to the ‘Kc’ (Kp-critical) value for my setup is a bit more difficult than normal, as the PID engine only operates for a few seconds, from the time the IR homing beacon is detected, to the time the robot actually connects (or doesn’t) to the charging probe. Here’s a short video showing a typical run (Kd = 150 in this case), and an Excel plot of the steering value from the same run.

As can be seen from the above, there really isn’t much of an ‘oscillation’ to go on – there is basically only one full cycle from about 10.5 sec to around 12.0 sec.

Here’s another run, this time with Kd set to 200. As can be seen, this is much more like what I was expecting to see, with several full cycles of oscillation. The amplitude trails off a bit toward the end, but this may have been due to a low battery level – I’ll have to repeat this experiment after getting a full charge into the robot.

Kp = 200, Kd = Ki = 0. Period is approximately 1.3 sec

However, using the above data with Kc = 200, we get

I revised my program to incorporate the Z-N numbers from the above calculations, and this resulted in the homing runs shown below; in the first one, Wall-E2 was oriented directly at the charging station beacon, and the robot’s track was pretty much direct, with no side-side oscillation at all. In the second one I oriented the robot a bit off-axis to excite a more active homing response. In both runs, the LEDs on the rear of the robot show the current relative wheel speed commands – LED’s to the left of center indicate higher wheel speed on the left, and vice versa. In the first run, the LEDs show that there is some oscillation of wheel speed commands, but it is relatively small, leading to an almost serene homing performance. In the second run the initial orientation offset forces the robot to more actively manage the wheel speeds to stay ‘on the beam’.

Stay tuned,

Frank