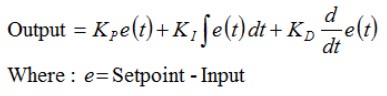Tag Archives: PID

More Wall Track PID Tuning Work

1 Reply

Posted 15 October 2022

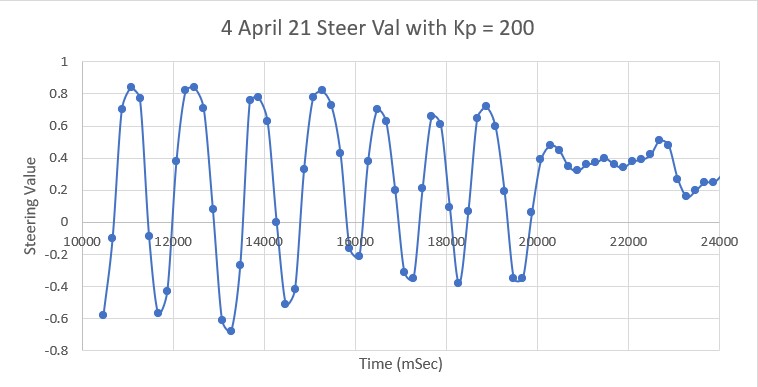
While working on my new ‘RunToDaylight’ algorithm for WallE3, my autonomous wall-following robot, I noticed that when WallE3 finds a wall to track after travelling in the direction of most front distance, it doesn’t do a very good job at all, oscillating crazily back and forth, and sometimes running head-first into the wall it is supposedly trying to track. This is somewhat disconcerting, as I thought I had long ago established a good wall tracking algorithm. So, I decided to once again plunge headlong into the swamps and jungles of my wall-tracking algorithm, hoping against hope that I won’t get eaten by mosquitos, snakes or crocodiles.

I went back to my latest part-task program, ‘WallE3_WallTrackTuning’. This program actually does OK when the robot starts out close to the wall, as the ‘CaptureWallOffset()’ routine is pretty effective. However, I noticed that when the robot starts out within +/- 4cm from the defined offset value, it isn’t terribly robust; the robot typically just goes straight with very few adjustments, even as it gets farther and farther away from the offset distance – oops!

So, I created yet another part-task program ‘WallE3_WallTrackTuning_V2’ to see if I could figure out why it isn’t working so well. With ‘WallE3_WallTrackTuning’ I simply called either TrackLeftWallOffset() or TrackRightWallOffset() and fed it the user-entered offset and PID values. However, this time I decided to pare down the code to the absolute minimum required to track a wall, as shown below (user input code not shown for clarity):

The big change from previous versions was to go back to using the desired offset distance as the setpoint for the PID algorithm, and using the measured distance from the (left or right) center VL53L0X sensor as the input to be controlled. Now one might be excused from wondering why the heck I wasn’t doing this all along, as it does seem logical that if you want to control the robot’s distance from the near wall, you should use the desired distance as the setpoint and the measured distance as the input – duh!

Well, way back in the beginning of time, when I changed over from dual ultrasonic ‘Ping’ sensors to dual arrays of three VL53L0X LIDAR sensors well over 18 months ago, I wound up using a combination of the ‘steering value’ ( (front – rear)/100 ) and the reported center distance – desired offset as the input to the PID calc routine, as shown in the following code snippet:

This is the line that calculates the input value to the PID:

This actually worked pretty well, but as I discovered recently, it is very difficult to integrate two very different physical mechanisms in the same calculations – almost literally oranges and apples. When the offset is small, the steering value term dominates and the robot simply continues more or less – but not quite – parallel to the wall, meaning that it slowly diverges from the desired offset – getting closer or further away. When the divergence gets large enough the offset term dominates and the robot turns toward the desired offset, but it is almost impossible to get PID terms that are large enough to actually make corrections without being so large as to cause wild oscillations.

The above problem didn’t really come to a head until just recently when I started having problems with tracking where the robot started off at or close to the desired offset value and generally parallel, meaning both terms in the above expression were near zero – for this case the behavior was a bit erratic to say the least.

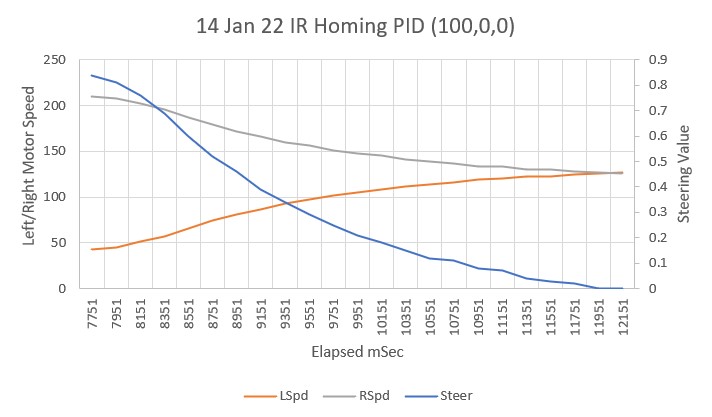
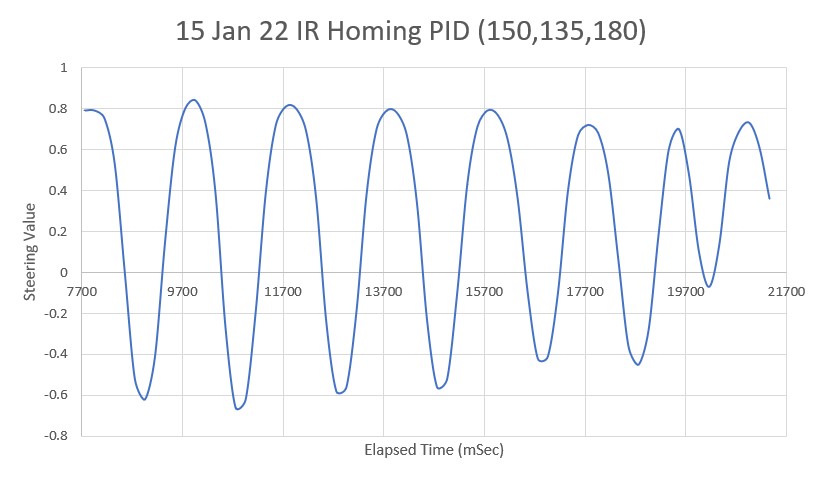
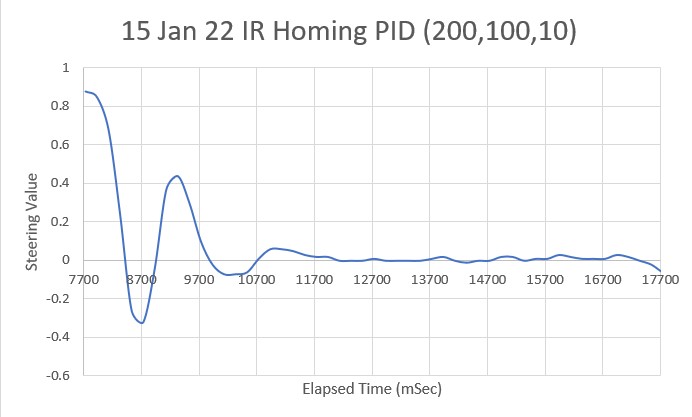
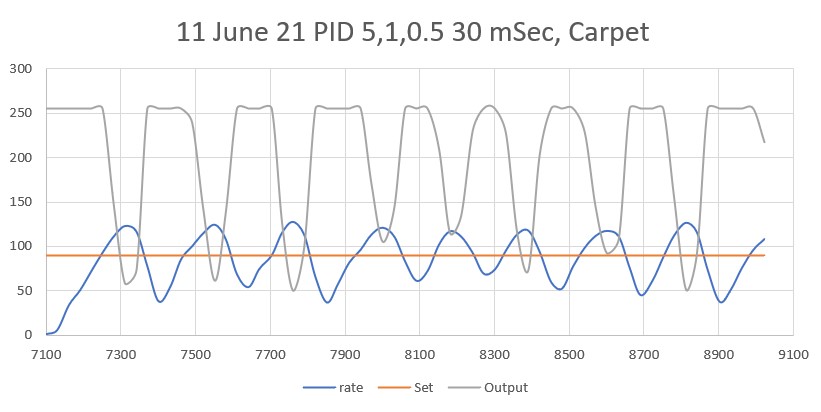
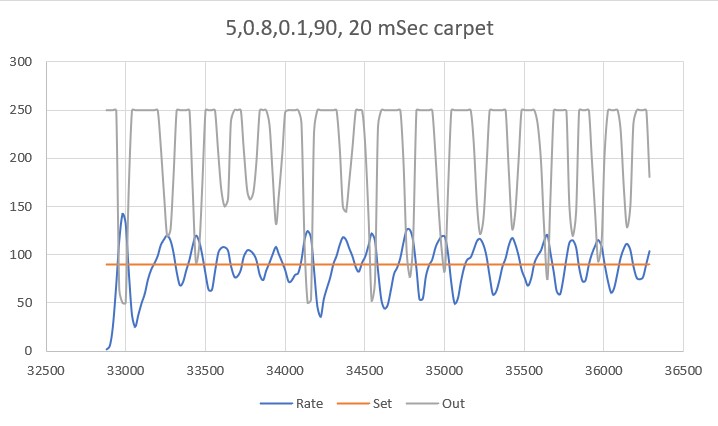
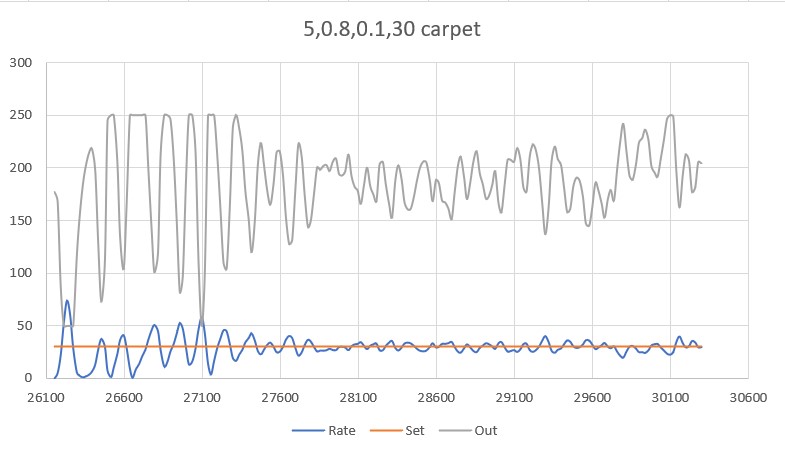
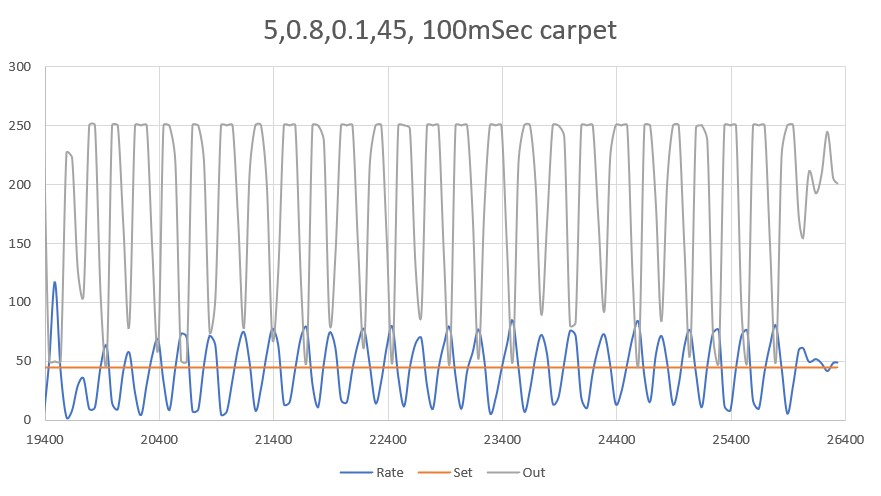
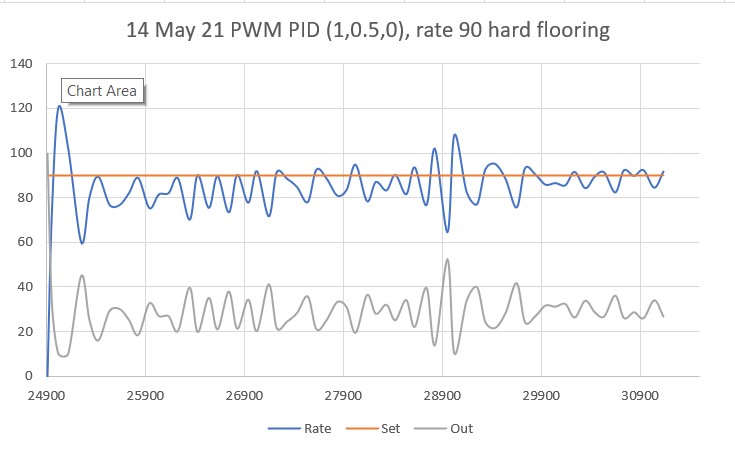
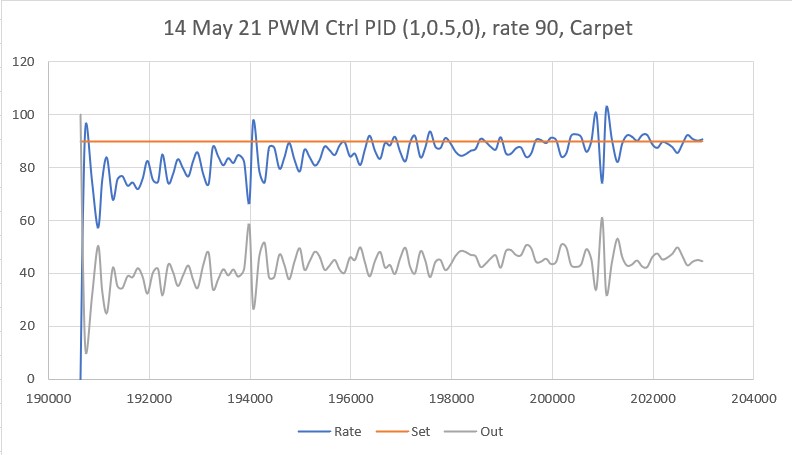
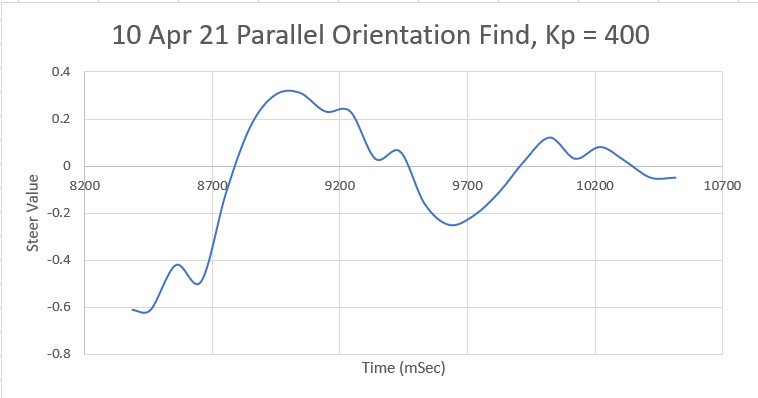
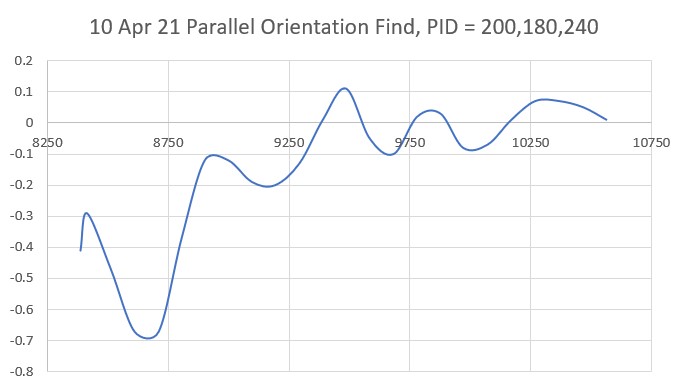
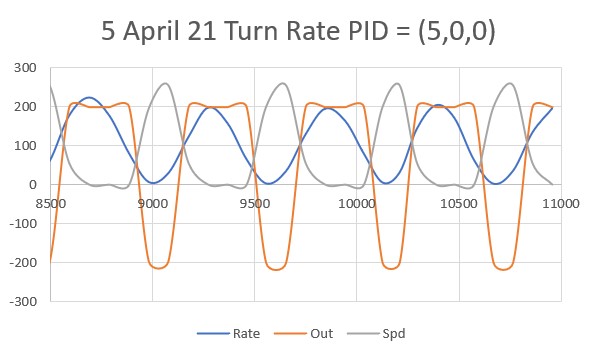
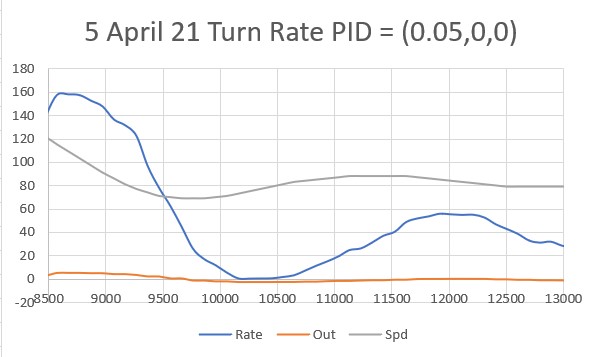
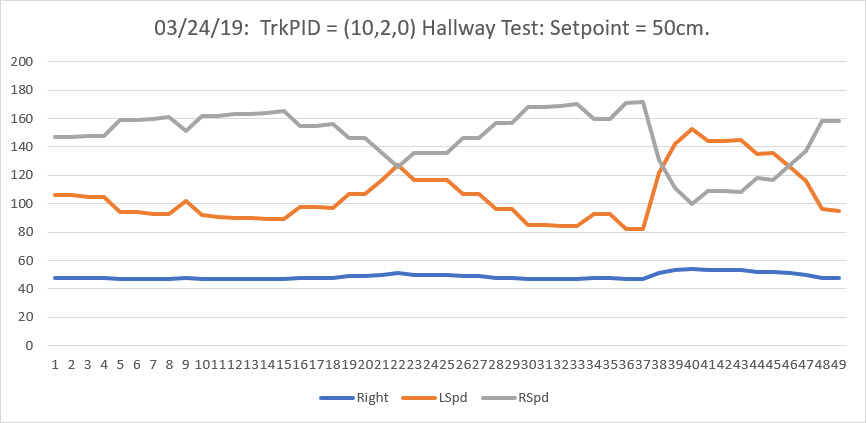
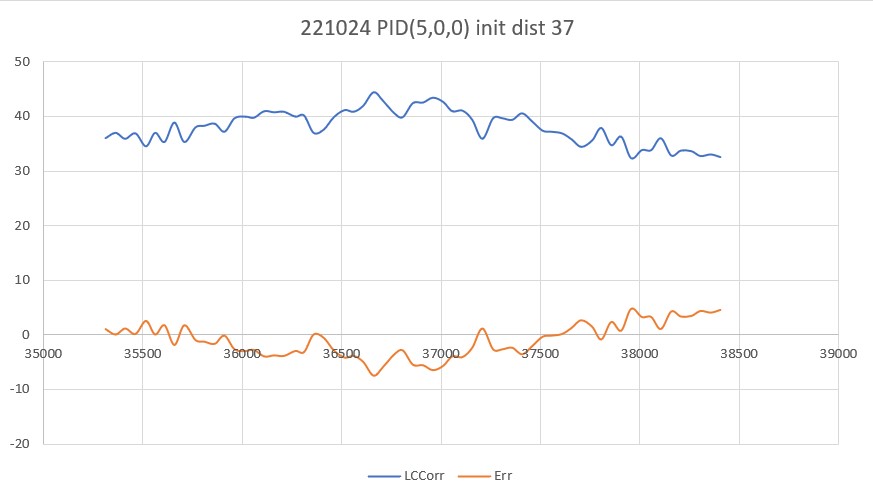
So, back to the basics. The following plot and short video show the robot’s behavior with the new setup (offset = 40cm, PID = (10,0,0)):

Tracking left wall with desired offset = 40cm
Desired offset = 40cm, PID = (10,0,0)

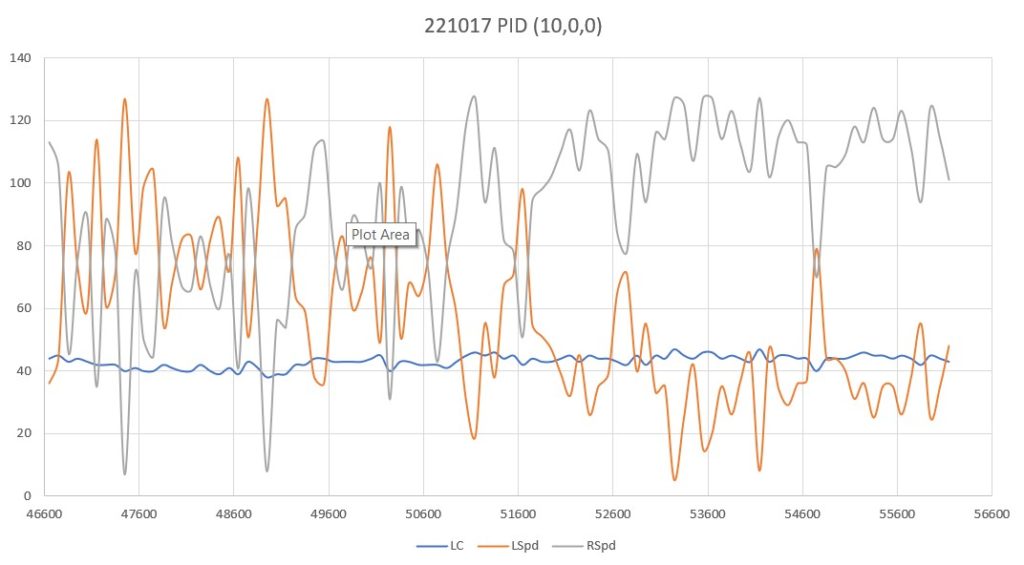
With this setup, the robot tracks the desired 40cm offset very well (average of 41.77cm), with a very slow oscillation. I’m sure I can tweak this up a bit with a slightly higher ‘P’ value and then adding a small amount of ‘I’, but even with the most basic parameter set the system is obviously stable.

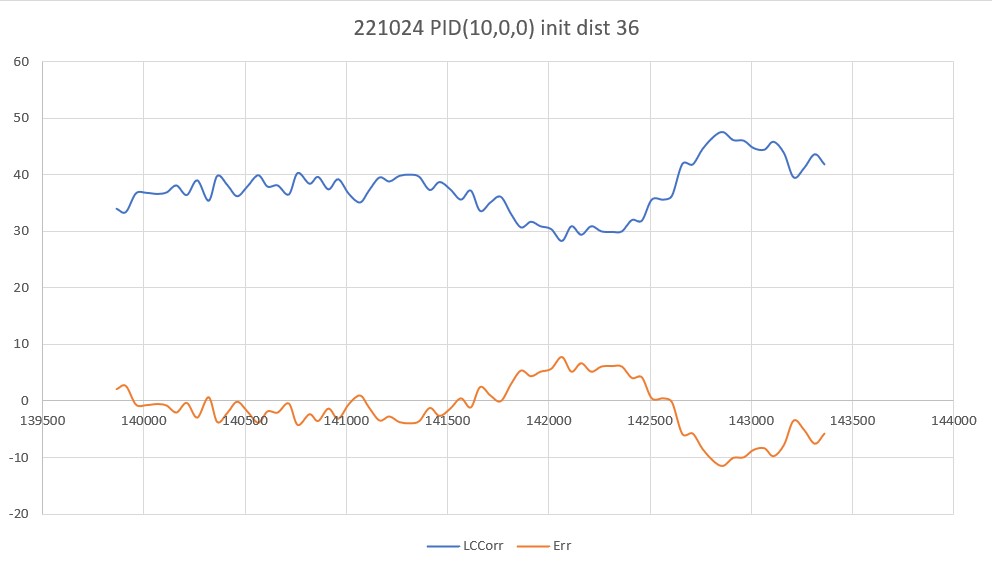
20 October 2022 Update:

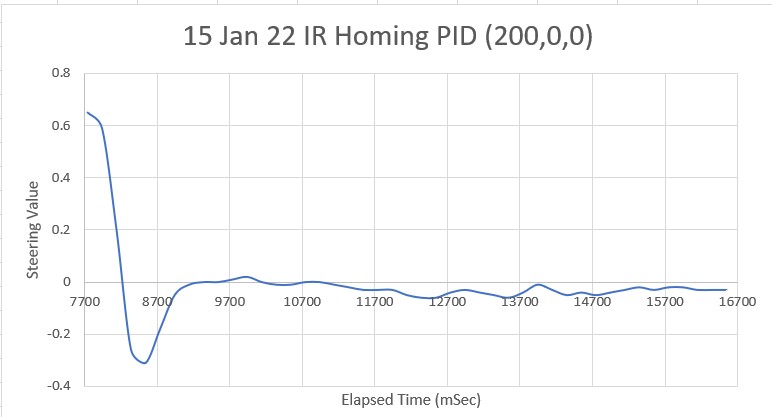
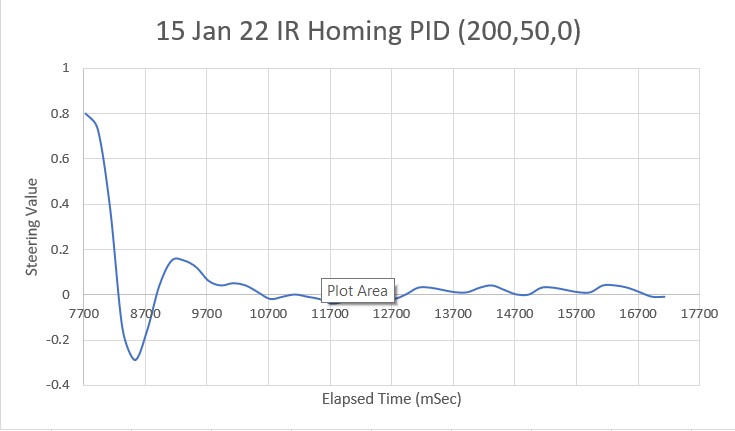
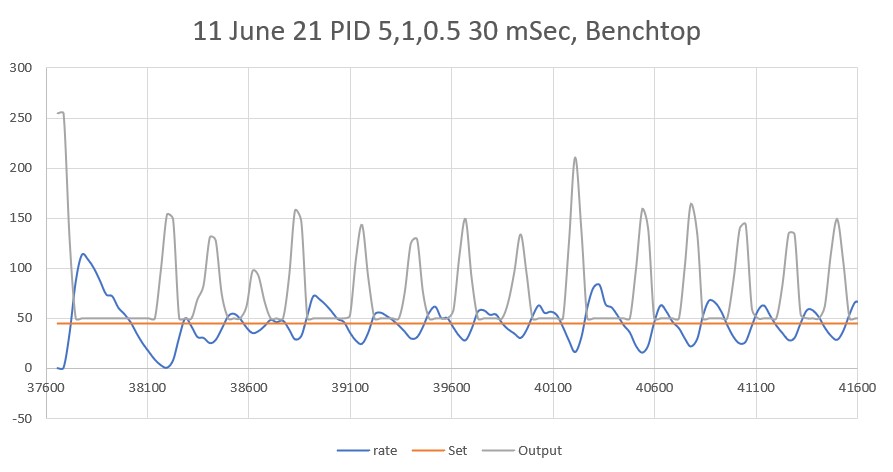
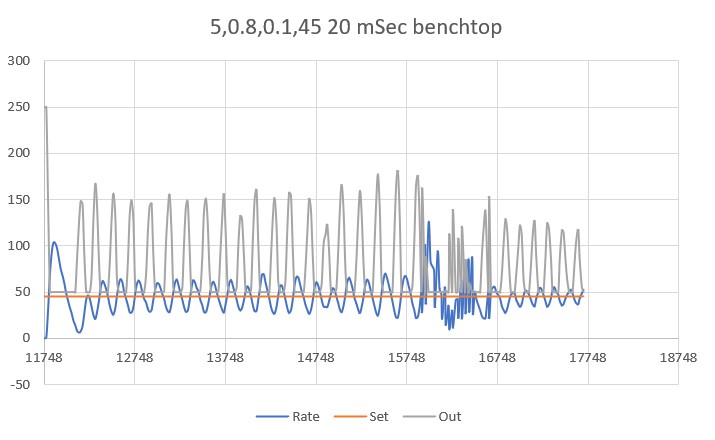
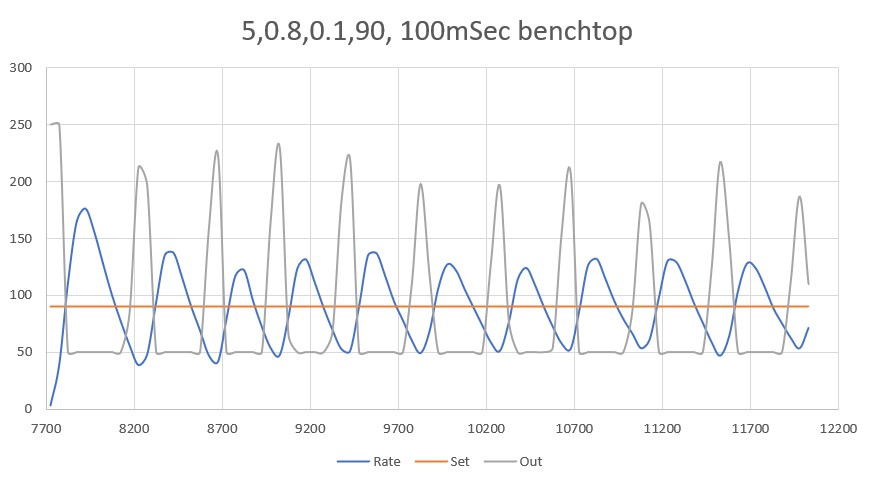
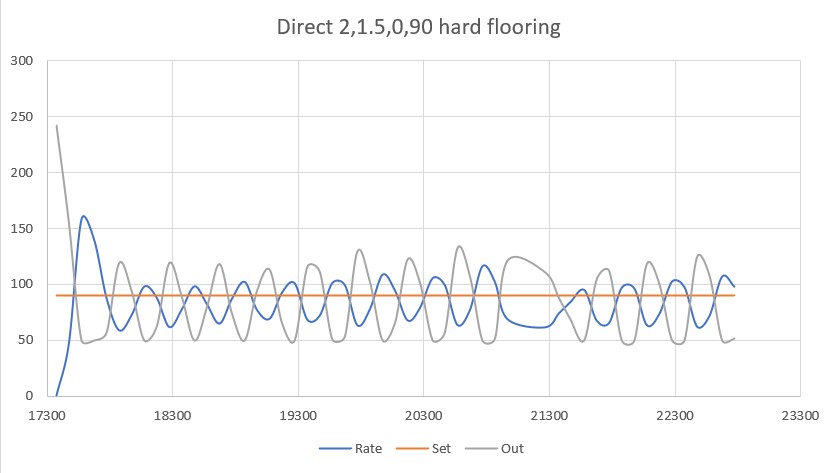
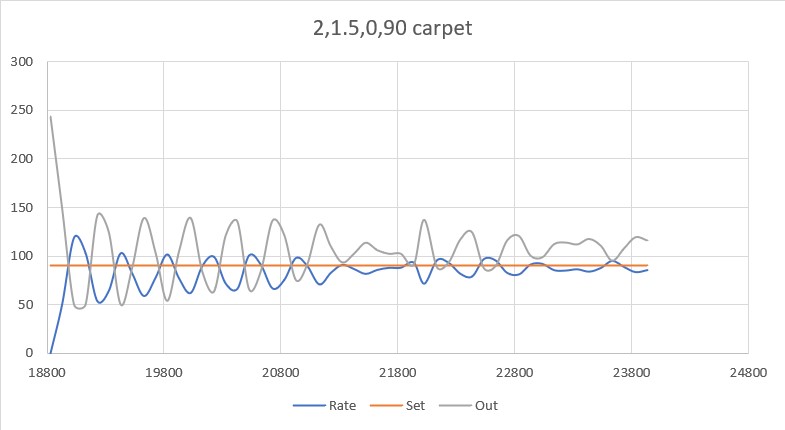
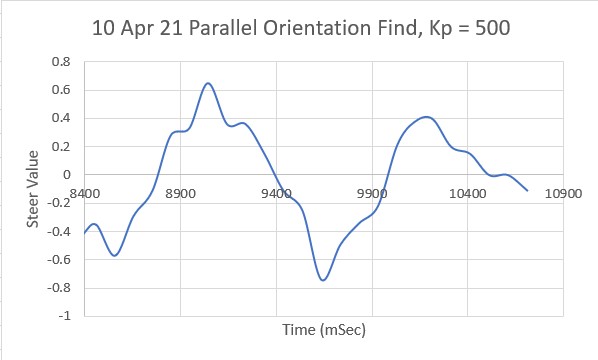
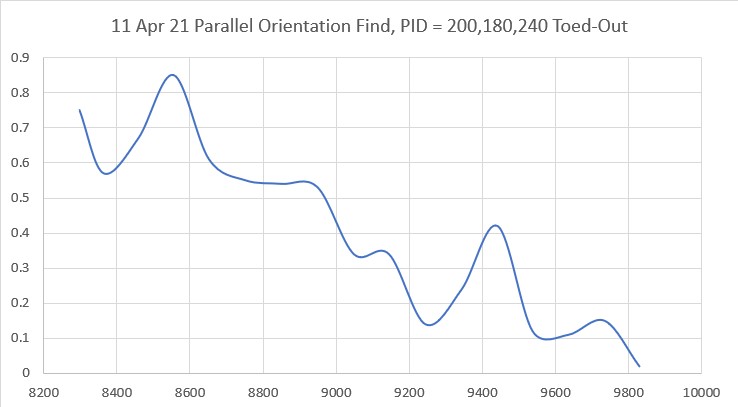
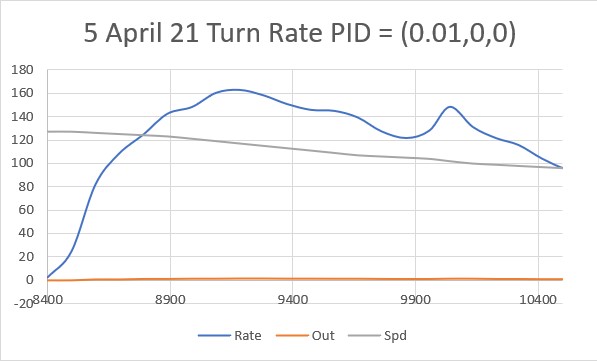
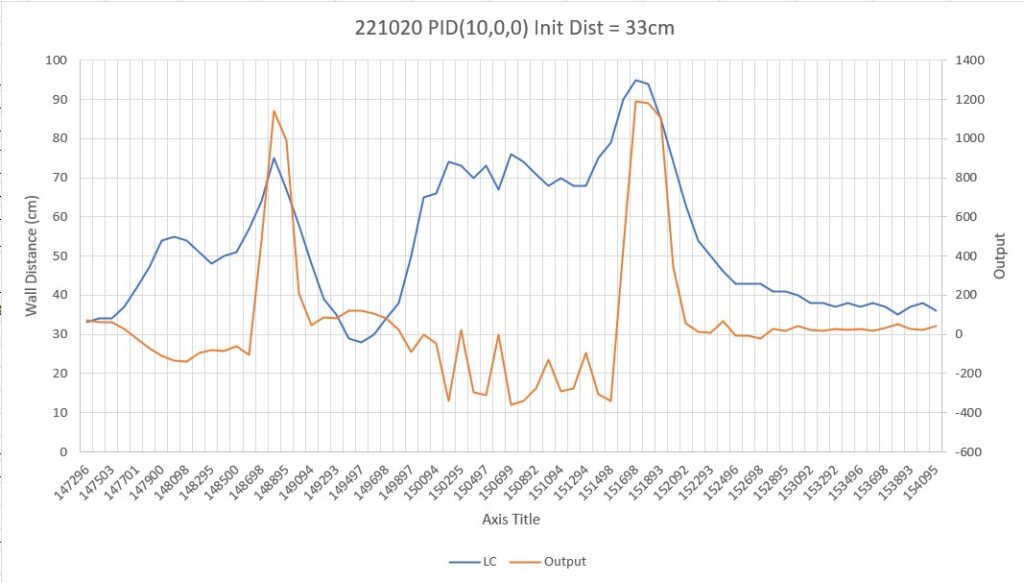
I made another run with PID(10,0,0), but this time I started the run with the robot displaced about 7cm from the 40cm offset. As shown in the plot and short video, this caused quite a large oscillation; not quite disastrous, but probably would have been if my test wall had been any longer.

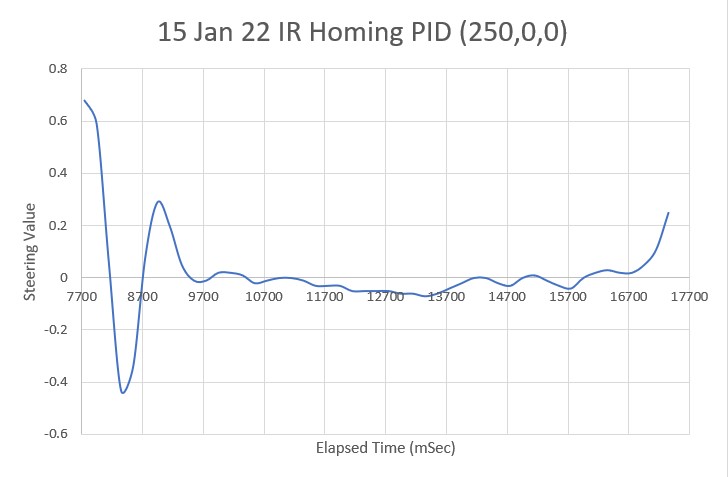
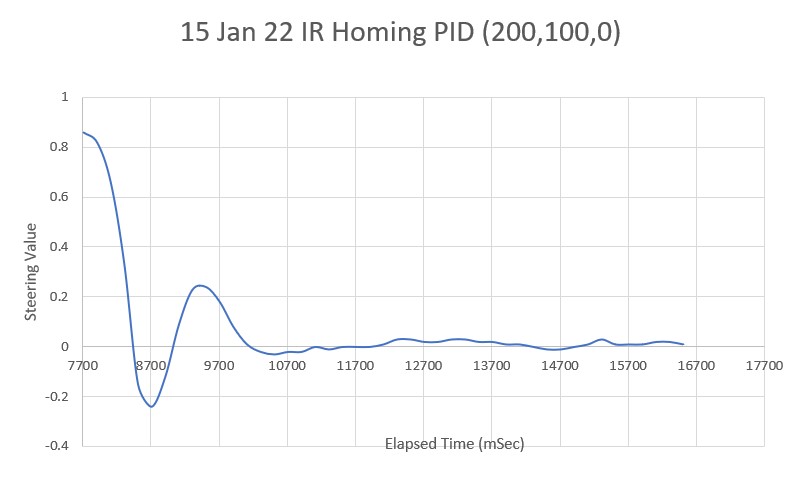
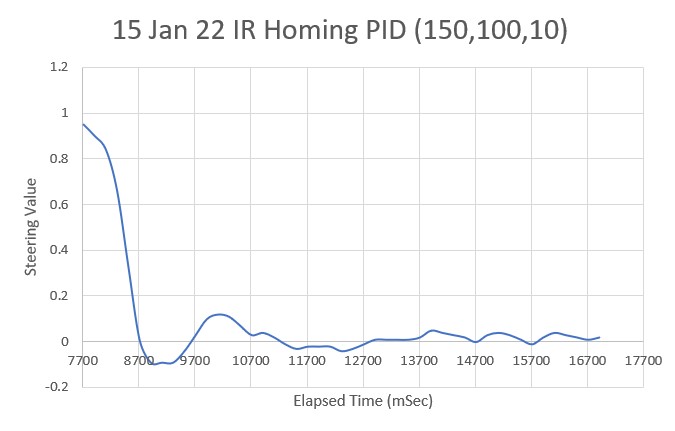
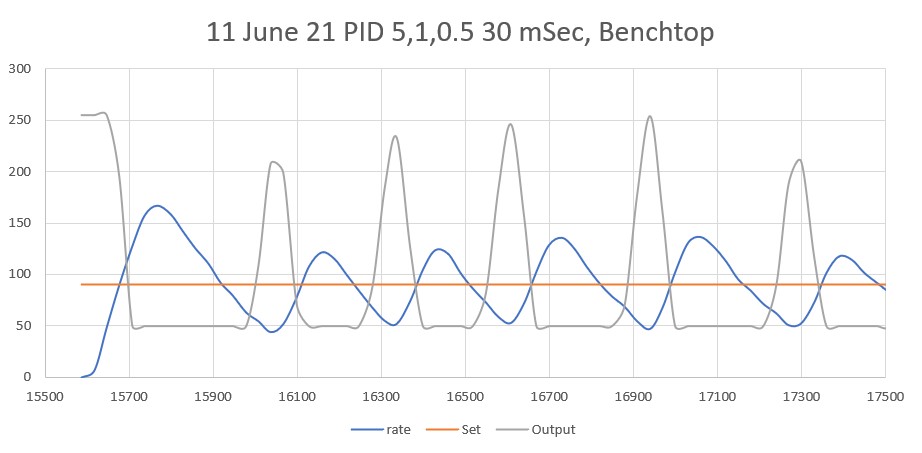
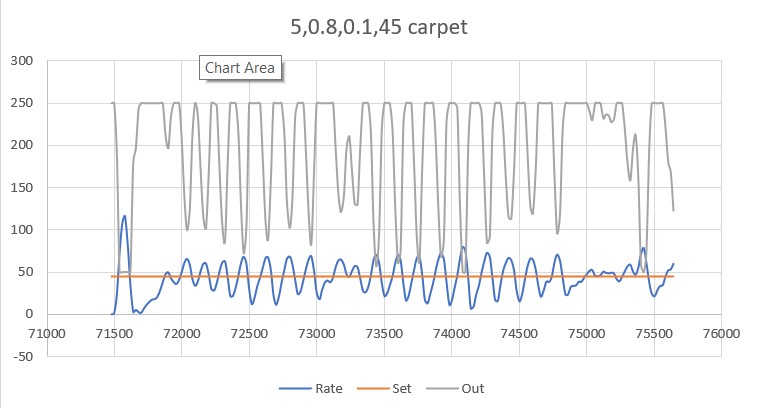
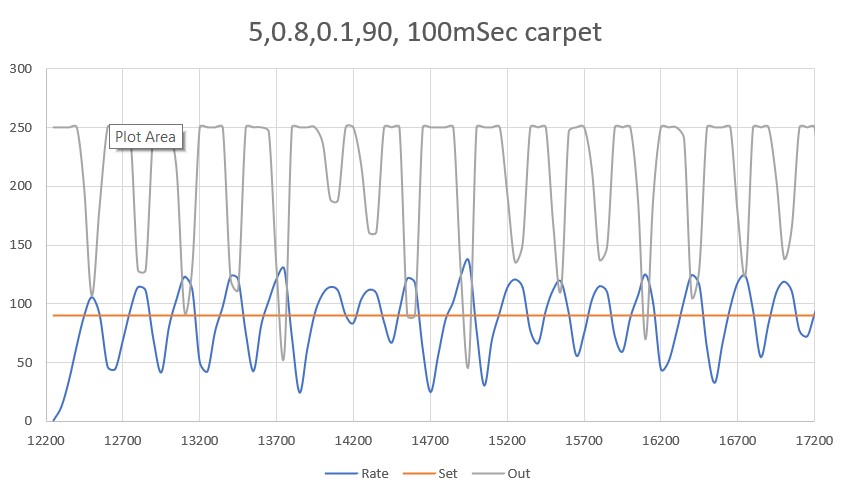
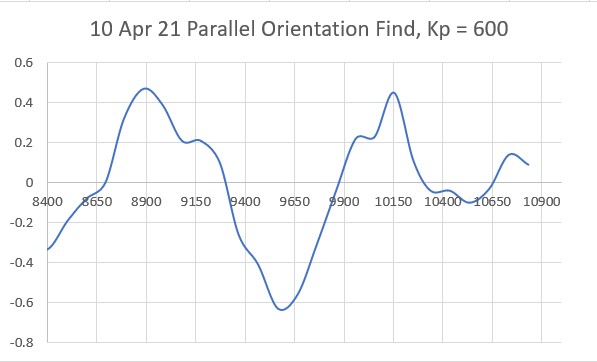
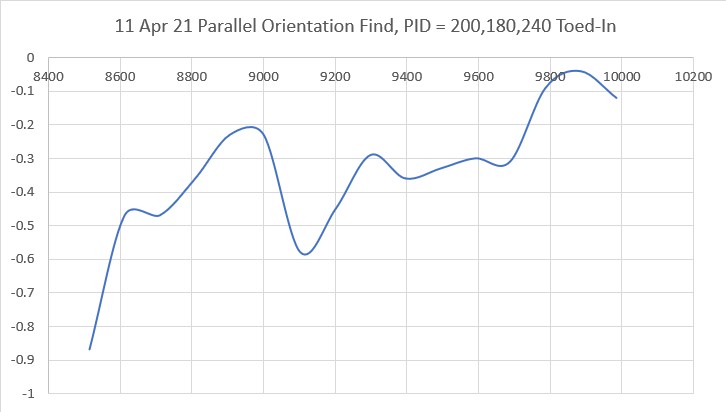
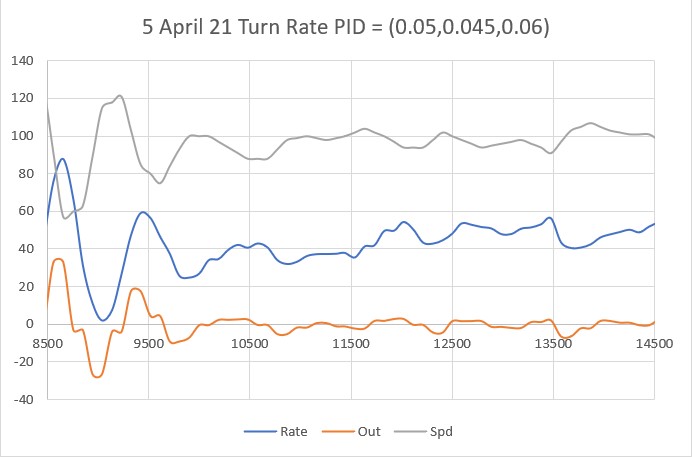
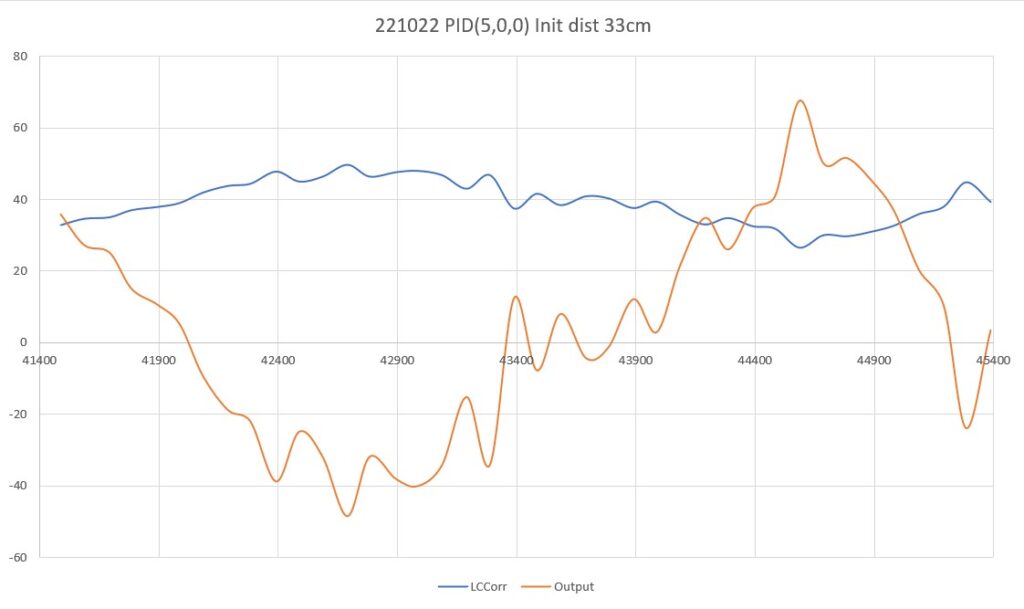
PID(10,0,0) with robot initial distance from wall = 33cm
PID(10,0,0) with initial position at 33cm

After looking at the data from this run, I decided to try lowering the P value from 10 to 5, thinking that the lower value would reduce the oscillation magnitude with a non-zero initial displacement from the desired setpoint. As the following plot and short video shows, the result was much better.

221022 PID(5,0,0) init dist 33cm
221022 PID(5,0,0) init dist 33cm

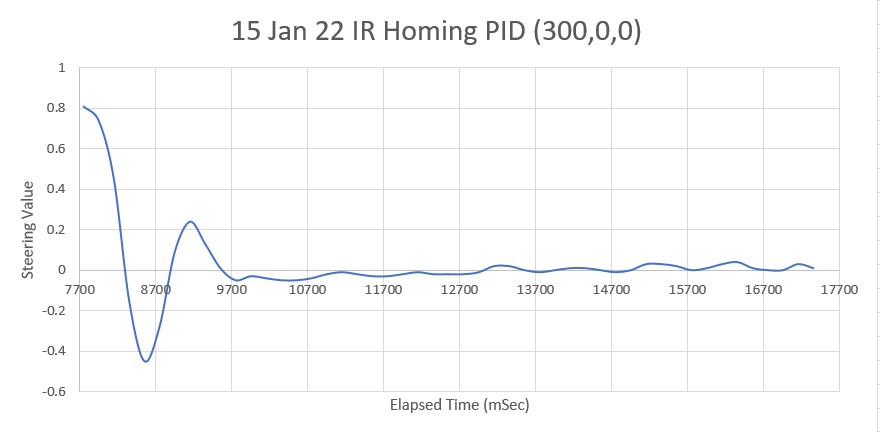
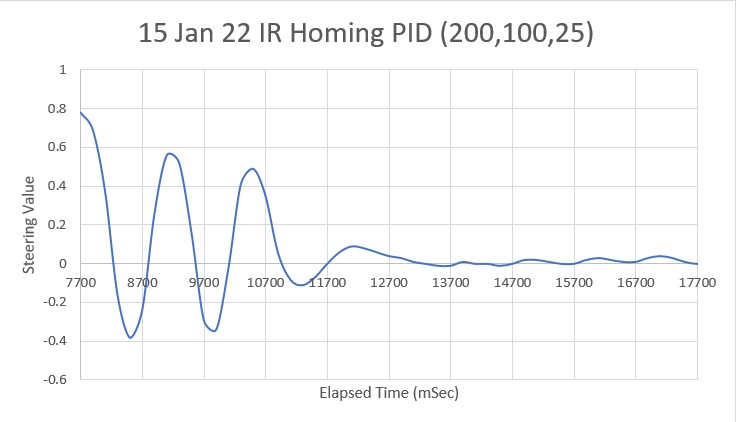
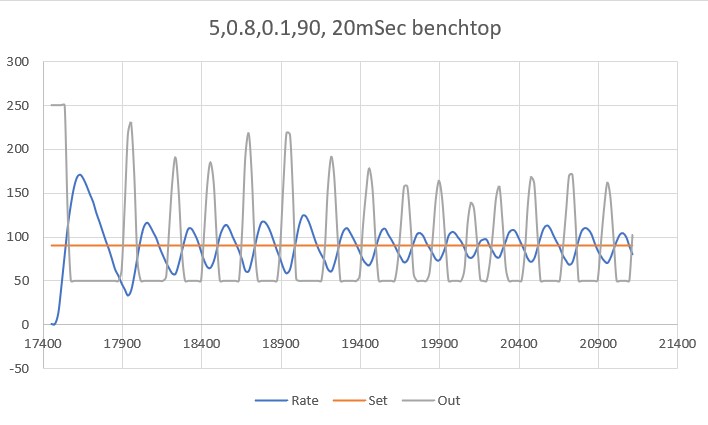
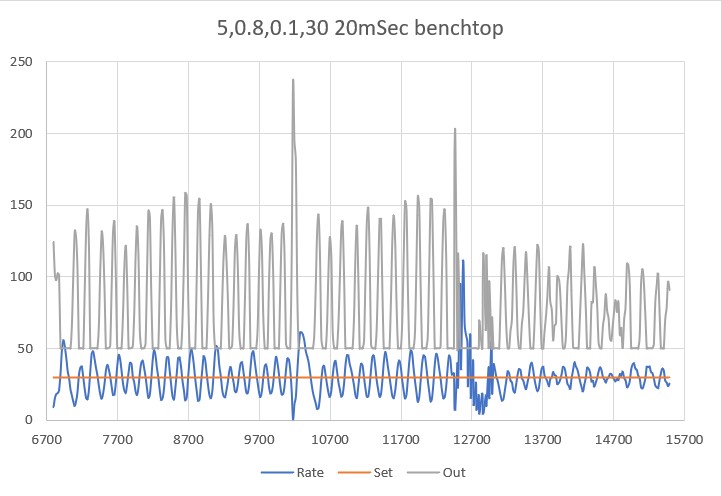
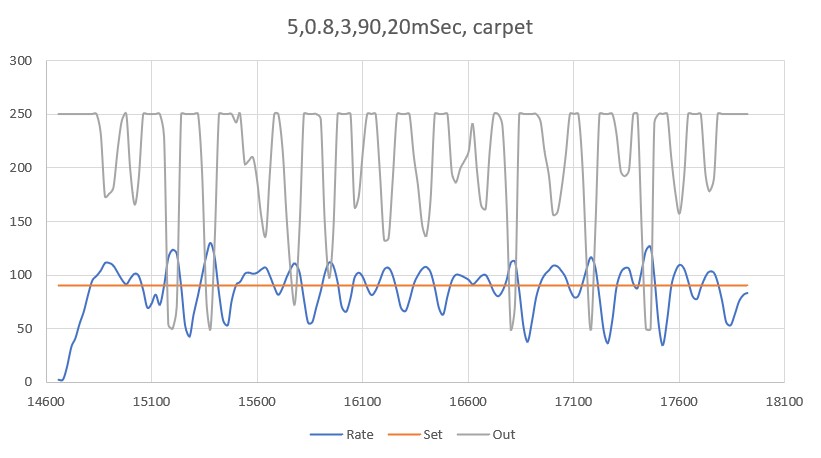
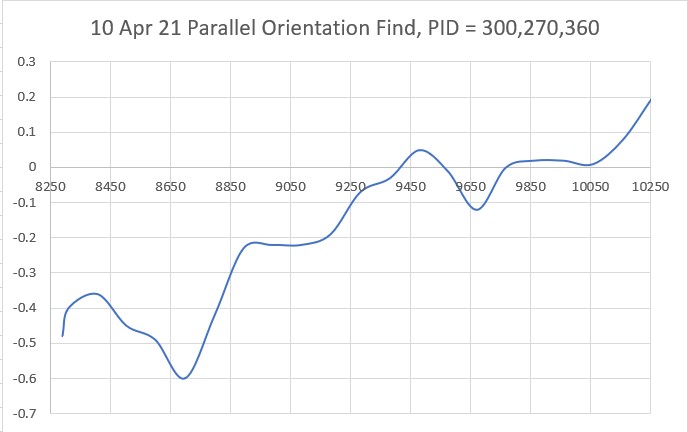
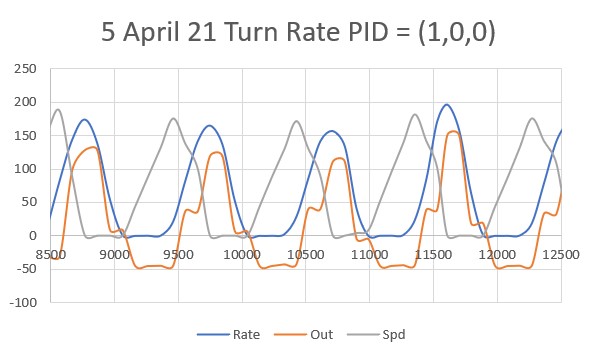
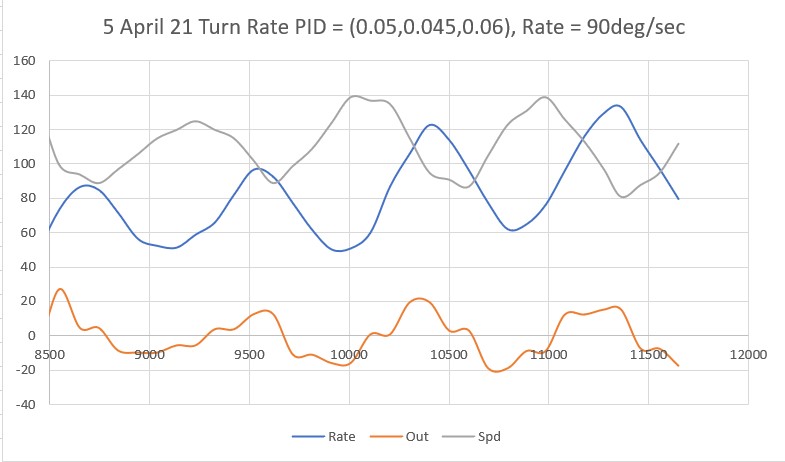
So then I tried PID(3,0,0), again with an initial placement of 33cm from the wall, 7cm from the setpoint of 40cm

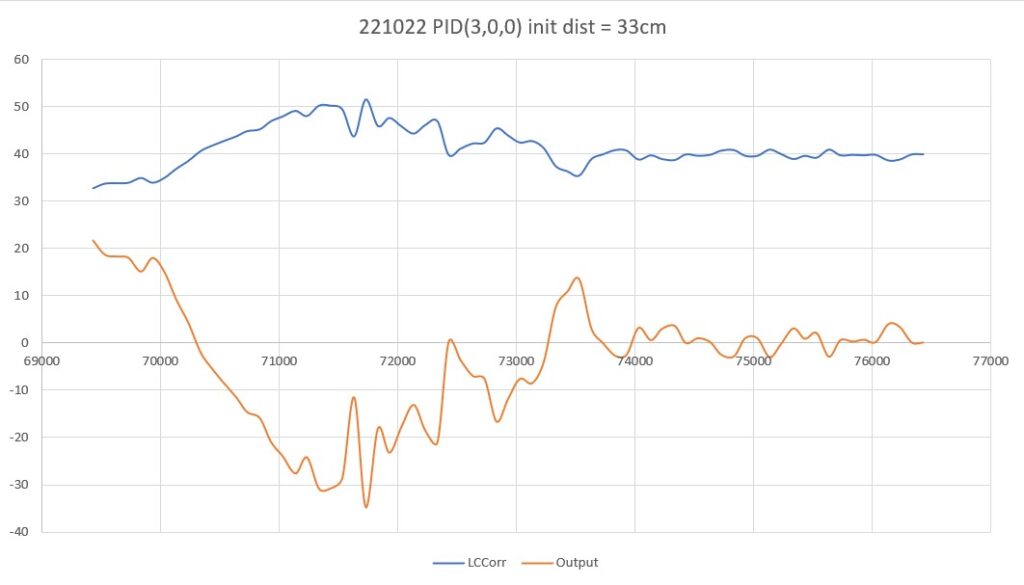
PID(3,0,0) init dist 33cm, avg for all points ~41.3cm
PID(3,0,0) init dist 33cm, avg for all points ~41.3cm

As shown by the plot and video, PID(3,0,0) does a very good job of recovering from the large initial offset and then maintaining the desired 40cm offset. This result makes me start to wonder if my separate ‘Approach and Capture’ stage is required at all. However, a subsequent run with PID (3,0,0) but with an initial placement of 15cm (25cm error) disabused me of any thoughts like that!

ouch!

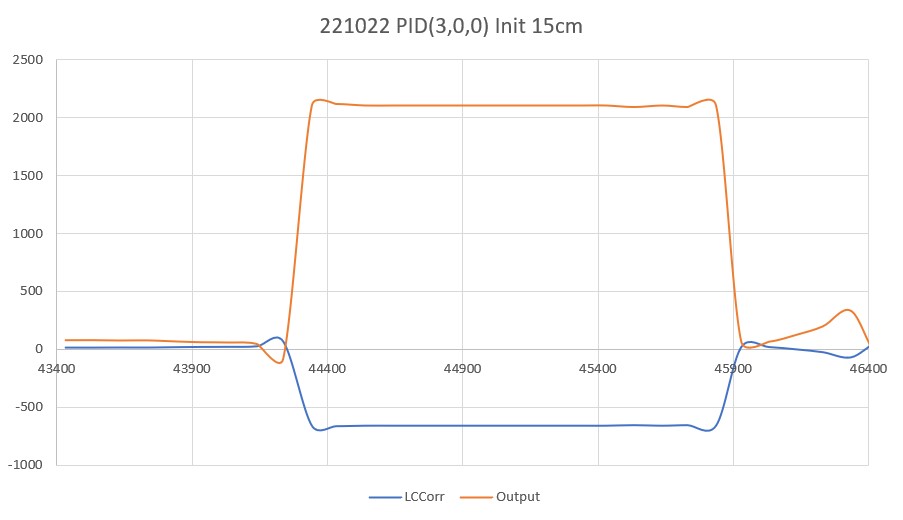
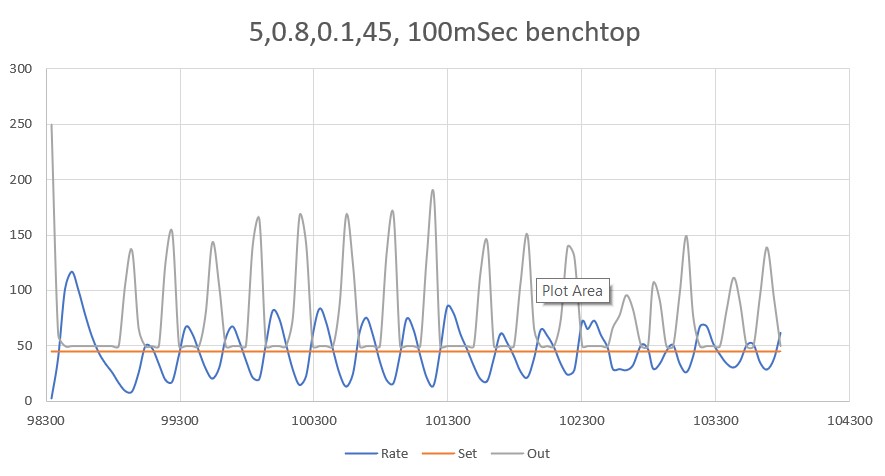
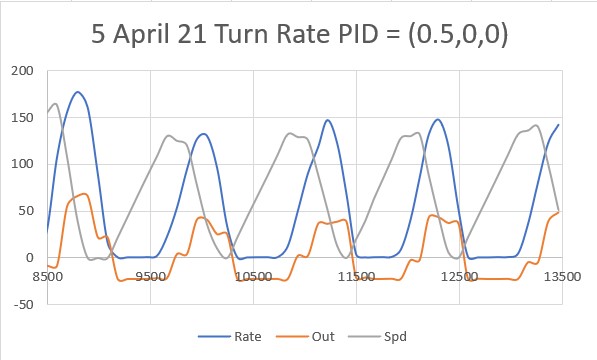
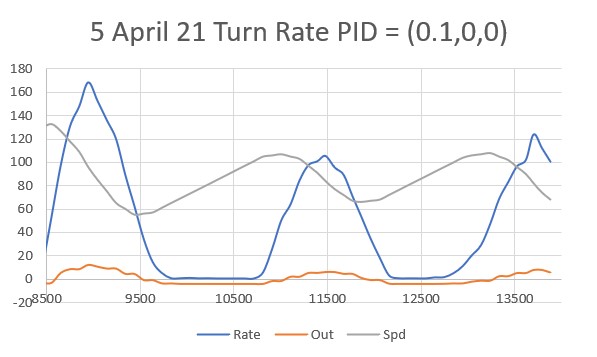
After talking this over with my PID-expert stepson, he recommended that I continue to decrease the ‘P’ term until the robot never quite gets to the desired setpoint before running out of room, and then adding some (possibly very small) amount of ‘D’ to hasten capture of the desired setpoint. So, I continued, starting with a ‘P’ value of 2, as shown below:

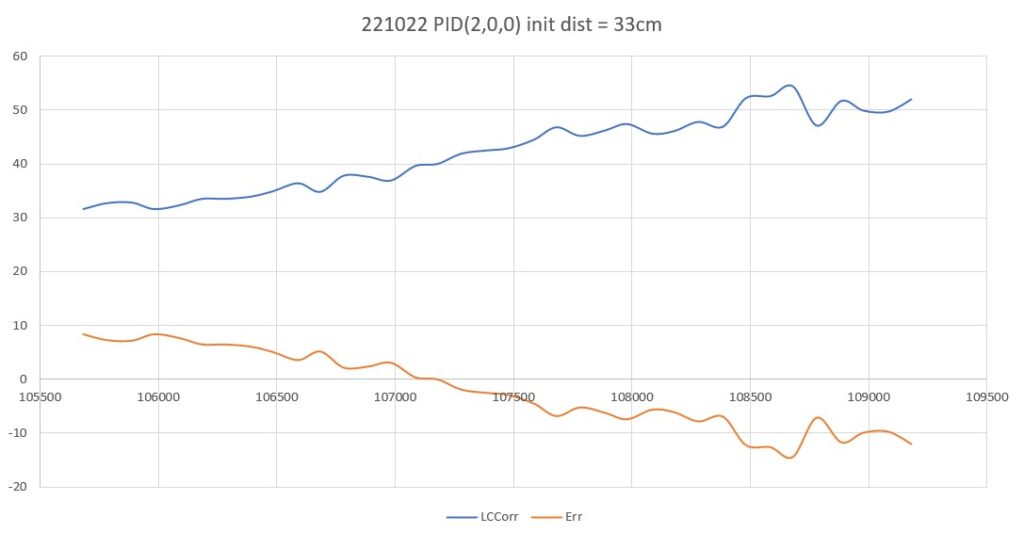
The ‘Err’ term is the actual PID error term, not multiplied by P as before

This result was a bit unexpected, as I thought such a ‘straight-line’ trajectory should have ended before going past the 40cm setpoint, indicating that I had achieved my ‘not quite controlling’ value of ‘P’. However, after thinking about a bit and looking at the actual data (shown below), I think what this shows is that the robot case is fundamentally different than most PID control applications in that reducing the error term (and thus the ‘drive’ signal) doesn’t necessarily change the robot’s trajectory, as the robot will tend to travel in a straight line in the absence of a contravening error term. In other words, removing the ‘drive’ due to the error term doesn’t cause the robot to slow down, as it would in a normal motor drive scenario.

23 October 2022 Update:

In previous work on this subject, I had already recognized that the ‘capture’ and ‘track’ phases of Wall-E’s behavior required separate treatment, and had implemented this with a ‘CaptureWallOffset()’ function to handle the ‘capture’ phase. This function calculates the amount of rotation needed to achieve an approximately 30 deg orientation angle with respect to the near wall, then moves forward to the desired wall offset value, and then turns back to parallel the near wall.

So, my next step is to re-integrate this ‘CaptureWallOffset()’ routine with my current distance-only based offset tracking algorithm. The idea is to essentially eliminate the problem space where the distance-only PID algorithm fails, so the PID only has to handle initial conditions very near the desired setpoint. When the ‘CaptureWallOffset()’ routine completes, the robot should be oriented parallel to the wall, and at a distance close to (but not necessarily the same as) the desired setpoint. Based on the above results, I think I will change the setpoint from the current constant value (40 cm at present) to match the measured distance from the wall at the point of ‘CaptureWallOffset()’ routine completion. This will guarantee that the PID starts out with the input matching the setpoint – i.e. zero error.

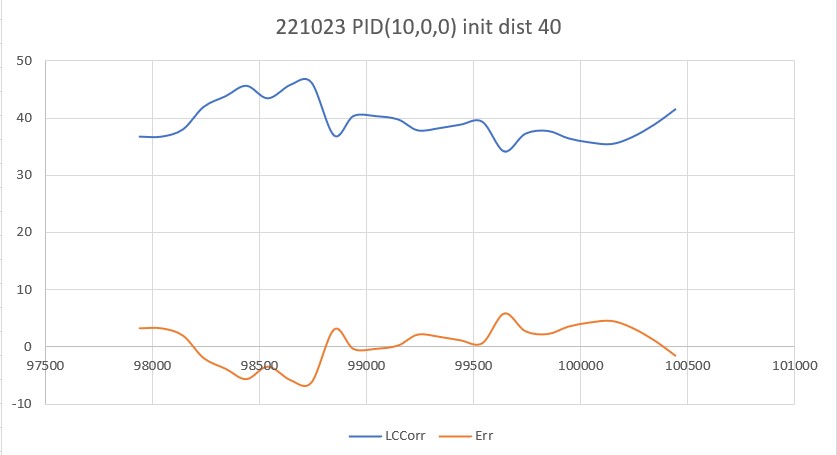
With this new setup, I made a run with the robot starting just 13cm from the wall. The CaptureWallOffset() routine moved the robot from the initial 13cm to about 37cm, with the robot ending up nearly parallel. The PID tracking algorithm started with an initial error term of +3.3, and tracked very well with a ‘P’ value of 10. See the plot and short video below. The video shows both the capture and track phases, but the plot only shows the track portion of the run.

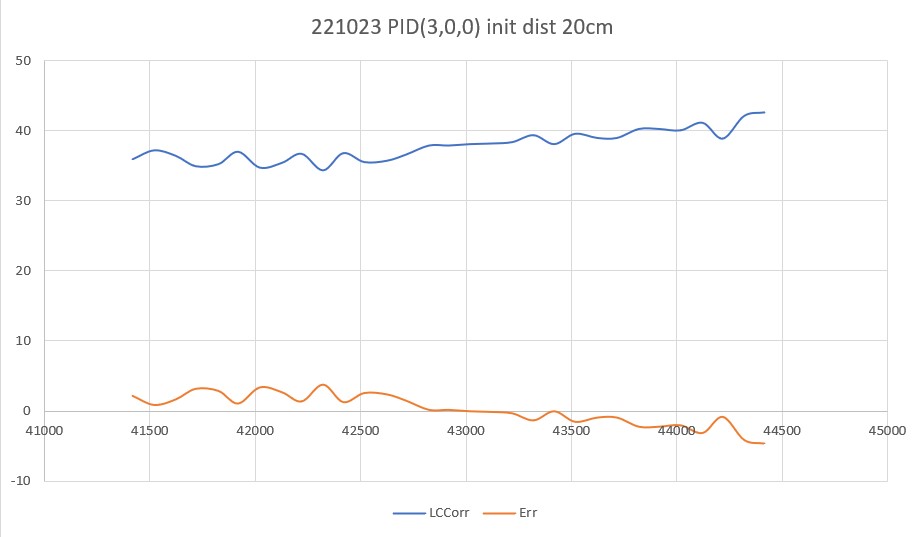
PID tracking after completion of CaptureWallOffset()

Here’s a run with PID(3,0,0), starting at an offset of 22cm.

24 October 2022 Update:

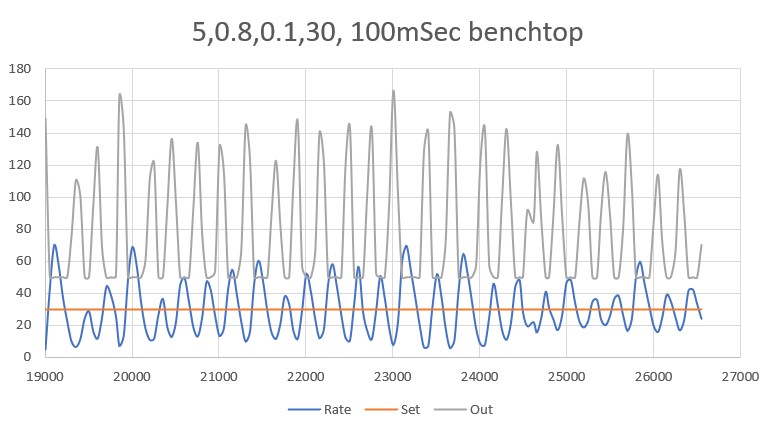
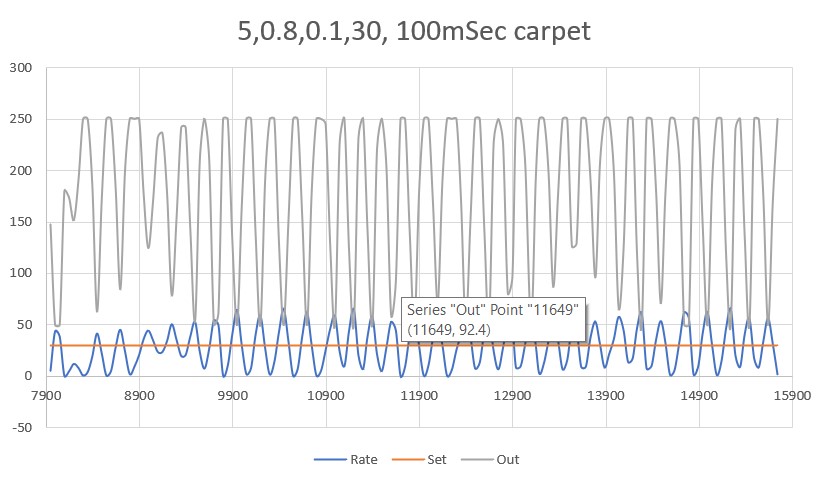
While reading through some more PID theory/practice articles, I was once again reminded that smaller time intervals generally produce better results, and that struck a bit of a chord. Some time back I settled on a time interval of about 200mSec, but while I was working with my ‘WallTrackTuning_V2’ program I realized that this interval was due to the time required by the PulsedLight LIDAR to produce a front distance measurement. I discovered this when I tried to reduce the overall update time from 200 to 100mSec and got lots of errors from GetFrontDistCm(). After figuring this out, I modified the code to use a 200mSec time interval for the front LIDAR, and 100mSec for the VL53L0X side distance sensors.

So, it occurred to me that I might be able to reduce the side measurement interval even further, so I instrumented the robot to toggle a digital output (I borrowed the output for the red laser pointer) at the start and end of the wall tracking adjustment cycle, as shown in the code snippet below:

Using my handy-dandy Hanmatek DSO, I was able to capture the pin activity, as shown in the following plot:

Wall track update cycle activity with 100mSec interval (20mSec/div)

As shown above, the update code takes a bit less than 20mSec to complete, and idles for the remaining 80mSec or so, waiting for the 100mSec time period to elapse. So, I should be able to reduce the time interval by at least a factor of two. I changed the update interval from 100mSec to 50mSec, and got the activity plot shown below:

Wall track update cycle activity with 50mSec interval (20mSec/div)

The above plot has the same 20mSec/div time scale as the previous one; as can be seen, there is still plenty of ‘idle’ time between wall tracking updates. Now to see if this actually changes the robot’s behavior.

As shown in the next plot and video, I ran another ‘sandbox’ test, this time with the update interval set to 50mSec vice 100mSec, and with an 11Cm initial offset.

PID(5,0,0), initial distance 11Cm
PID(5,0,0), initial distance 37Cm

Then I ran it again, except this time with a PID of (10,0,0):

PID(10,0,0), initial distance 11Cm
221024 PID(10,0,0) Init 36cm, LCorr

This wasn’t at all what I expected. I thought the larger ‘P’ value would cause the robot to more closely track the desired offset, but that isn’t what happened. Everything is fine for the first two seconds (140,000 to 142,000 mSec), but then the robot starts weaving dramatically- to the point where the motor values max out at 127 on one side and 0 on the other – bummer. Looks like I need another consulting session with my PID wizard stepson!

25 October 2022 Update:

My PID wiz stepson liked my idea of breaking the wall tracking problem into an offset capture phase, followed by a wall tracking phase, but wasn’t particularly impressed with my thinking about reducing the PID update interval while simultaneously increasing the P value to 10, so, I’m back to taking more data. The following run is just the wall tracking phase, with 50mSec update interval and a P value of 3.

As can be seen, the robot doesn’t really make any corrections – just goes in a straight line more or less. However, the left/right wheel speed data does show the correct trend (left wheel drive decreasing, right wheel drive increasing), so maybe a non-zero ‘I’ value would do the trick?

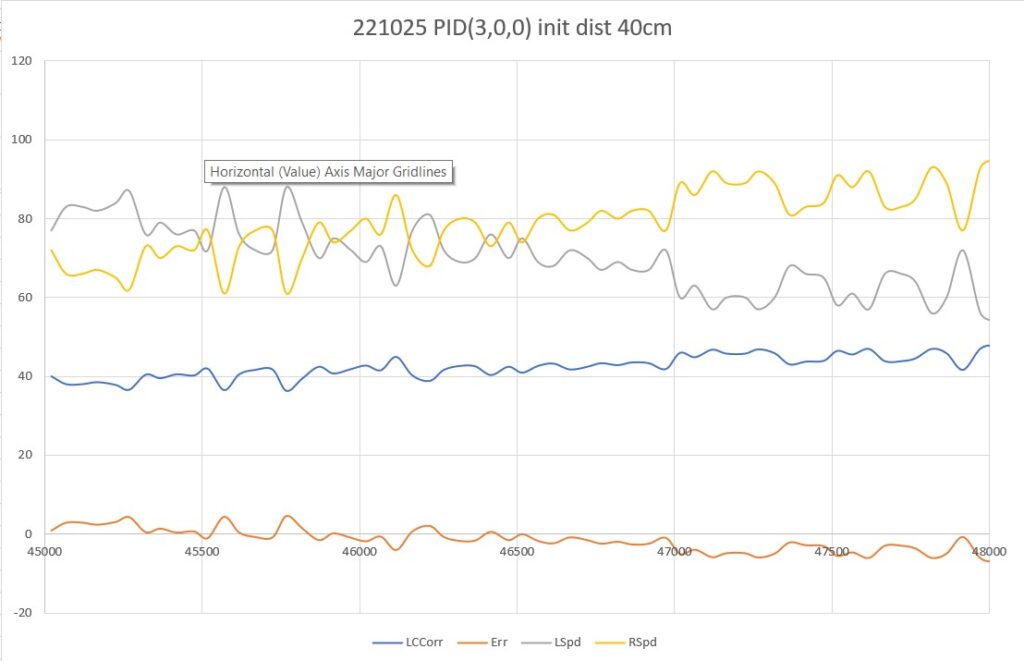
Here’s a run with PID(3,0.5,0):

PID(3,0.5,0) init dist 40cm

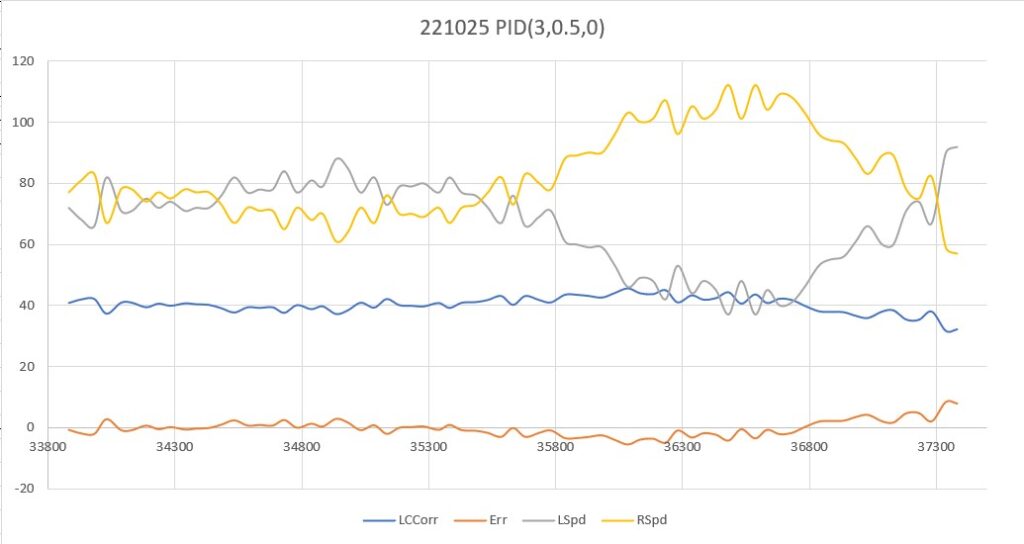
In the above plot the I value does indeed cause the robot to track back to the target distance, but then goes well past the target before starting to turn back. Too much I?

Here’s another run with PID(3,0.1,0) – looking pretty good!

PID(3,0.1,0) init dist 40cm

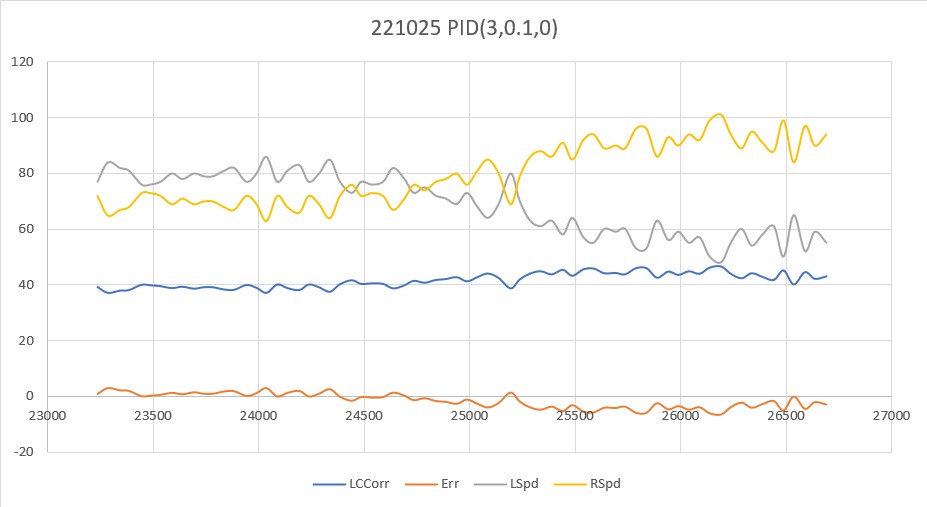
This looks pretty good; with I = 0.1 the robot definitely adjusted back toward the target distance, but in a much smoother manner than with I = 0.5. OK, time to let the master view these results and see if I’m even in the right PID universe.

One thing to mention in these runs – they are performed in my office, and the total run length is a little over 2m (210Cm), so I’m only seeing just one correction maneuver. Maybe if I start out with a small offset from the target value? Nope – that won’t work – at least not tonight; my current code changes the setpoint from the entered value (40Cm in this case) to the actual offset value (36Cm on this run) before starting the run. Curses! Foiled again!

27 October 2022 Update:

Today I had some time to see how the PID handles wall-tracking runs starting with a small offset from the desired value. First I started with a run essentially identical to the last run from two days ago, just to make sure nothing significant had changed (shouldn’t, but who knows for sure), as shown below:

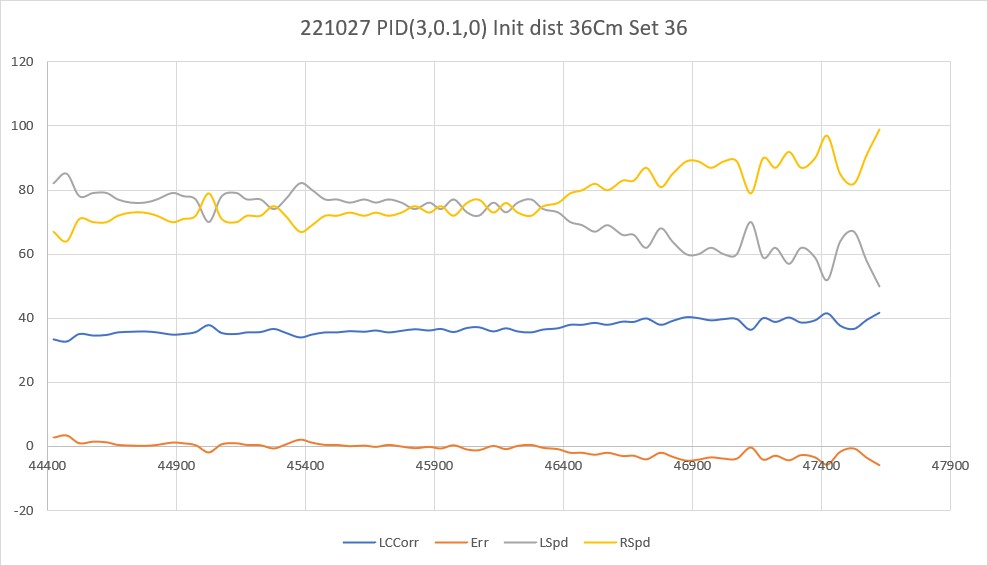
Then I tried a run with the same PID values, but with a small initial offset from the desired 40Cm:

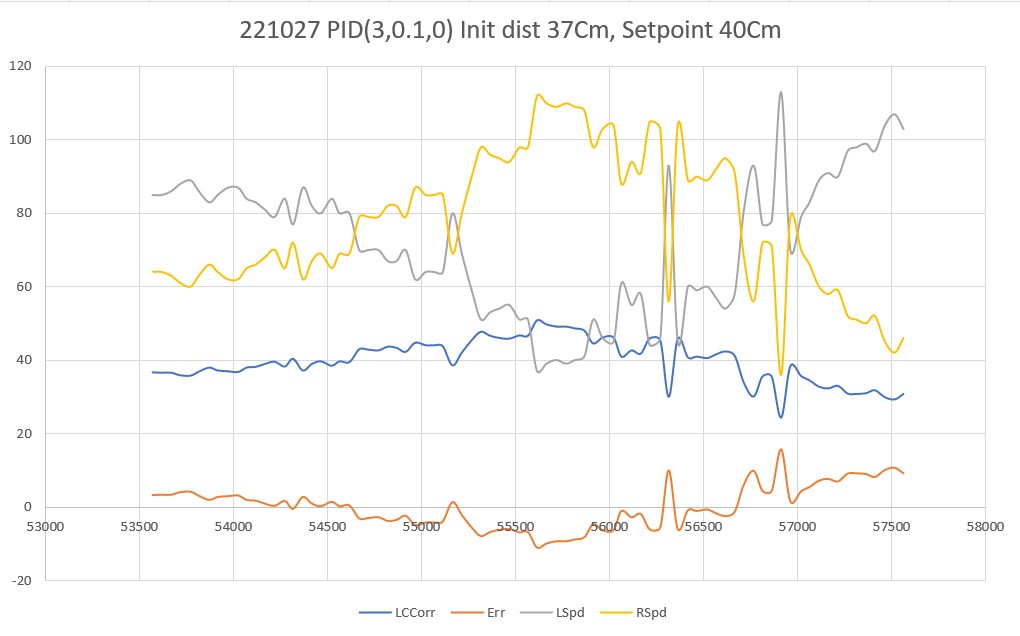
As can be seen, the robot didn’t seem to handle this very well; there was an initial correction away from the wall (toward the desired offset), but the robot cruised well past the setpoint before correcting back toward the wall. This same behavior repeated when the robot went past the setpoint on the way back toward the wall.

To see which way I needed to move with the ‘I’ value, a made another run with the ‘I’ value changed from 0.1 to 0.25, as shown below:

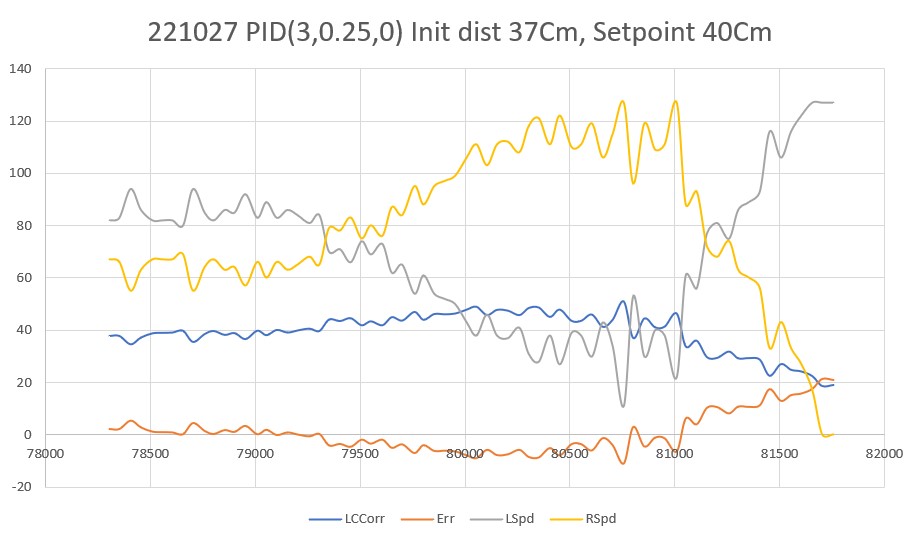
Now the corrections were much more dramatic, and tracking was much less accurate. on the second correction (when the robot passed through the desired setpoint going away from the wall), the motor drive values maxed out (127 on the left, 0 on the right).

Next I tried an ‘I’ value of 0.05, as shown below:

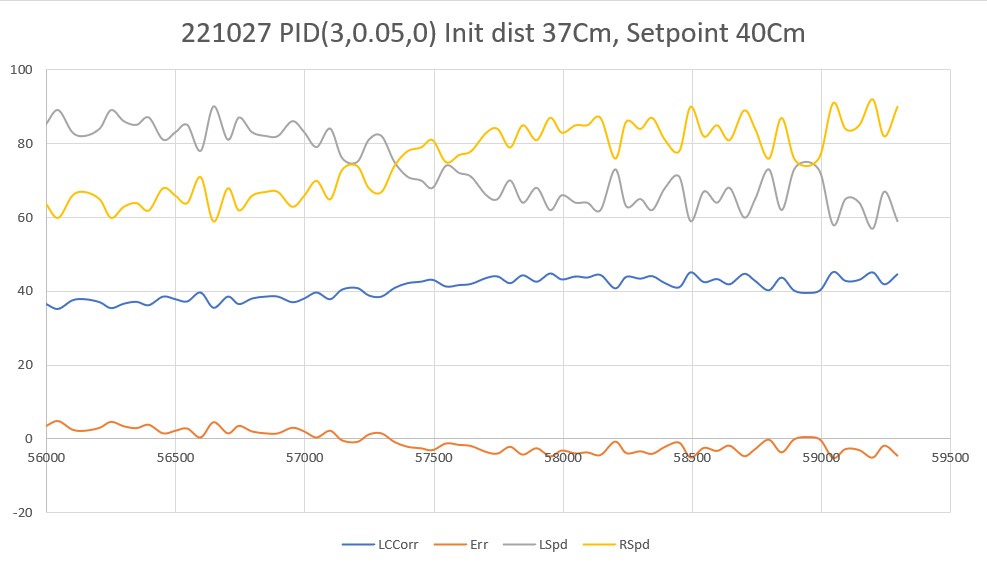
This looks much nicer – deviations from the desired offset are much smaller, and everything is much smoother. However, I’m a little reluctant to declare victory here, as it may well be that the ‘I’ value is so small now that it may not be making any difference at all, and what I’m seeing is just the natural straight-line behavior of the robot. In addition, the robot may not be able to track the wall around some of the 45deg wall direction changes found in this house.

28 October 2022 Update:

I decided to rearrange my office ‘sandbox’ to provide additional running room for my wall-following robot. By setting up my sandbox ‘walls’ diagonally across my office, I was able to achieve a run length of almost 4 meters (3.94 to be exact). Here is a plot and short video from a run with PID(3,0.1,0):

First run on my new 4m wall

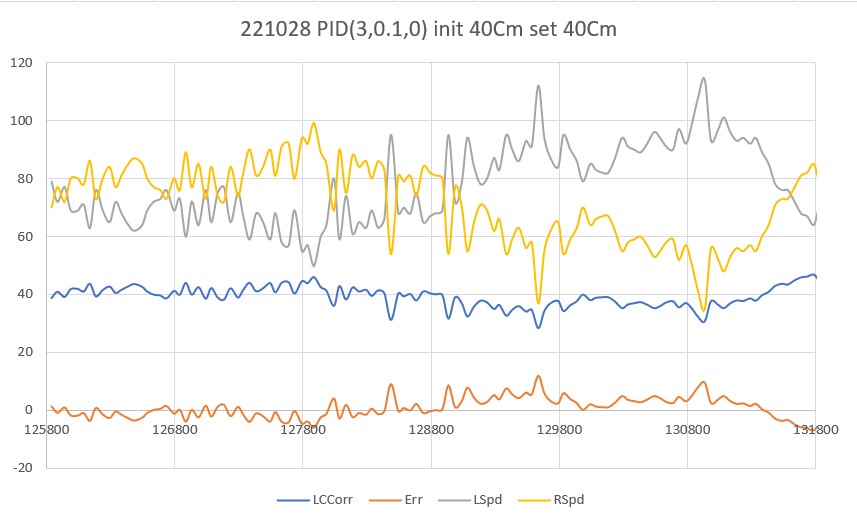
I was very encouraged by this run. The robot tracked very well for most of the run, deviating slightly at the very end. I’m particularly pleased by the 1.4sec period from about 129400 (129.4sec) to about 130800 (130.8sec); during this period the left & right wheel motor drive values were pretty constant, indicating that the PID was actively controlling motor speeds to obtain the desired the wall offset. I’m not sure what caused the deviation at the end, but it might have something to do with the ‘wall’ material (black art board with white paper taped to the bottom half) in that section. However, after replacing that section with white foam core, the turn-out behavior persisted, so it wasn’t the wall properties causing the problem.

After looking at the data and the video for a while, I concluded that the divergence at the end of the run was real. During the first part of the run, the robot was close enough to the setpoint so that no significant correction was required. However, as soon as the natural straight-line behavior diverged enough from the set point to cause the PID to produce a non-small output, the tracking performance was seriously degraded. In other words, the PID was making things worse, not better – rats.

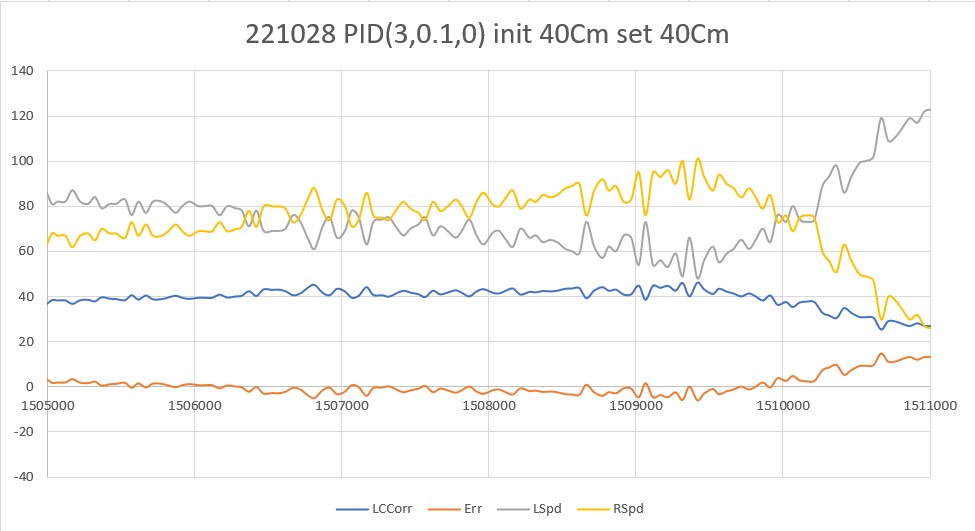
So, I tried another run, this time adding just a smidge of ‘D’, on the theory that this would still allow the PID to drive the robot back toward the setpoint, but not quite as wildly as before. With PID (3, 0.1, 0.1) I got the following plot:

Adding some ‘D’

As can be seen, things are quite a bit nicer, and the robot seemed to track fairly well for the entire 4m run.

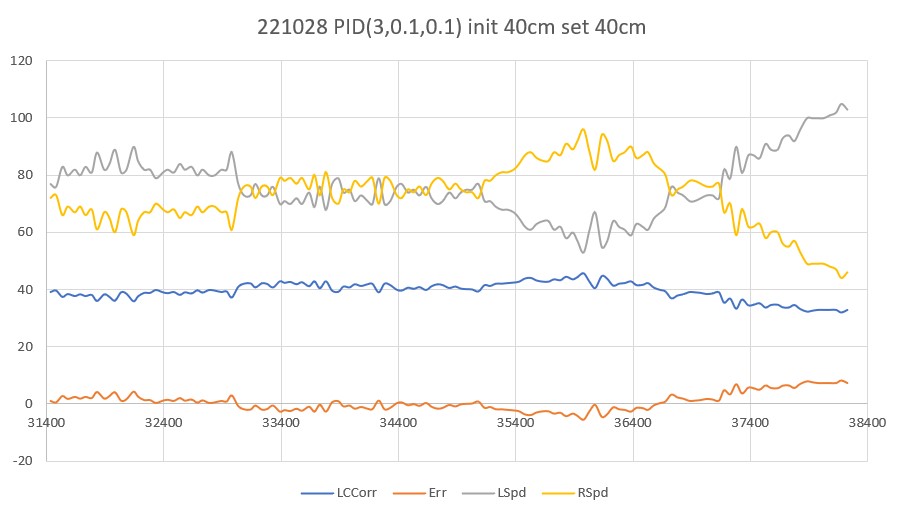
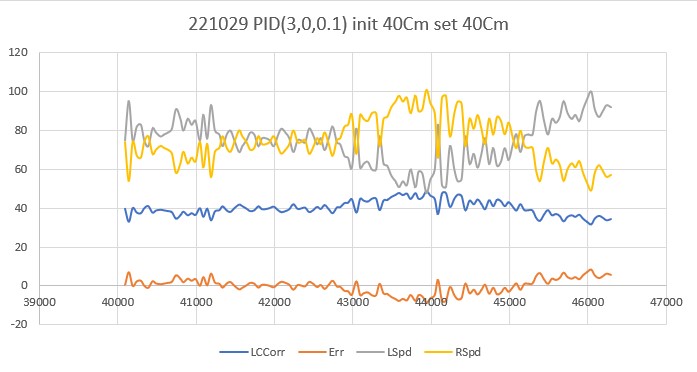
Tried another run this morning with PID(3,0,0.1), i.e. removing the ‘I’ factor entirely, but leaving the ‘D’ parameter at 0.1 as in my last run yesterday. As can be seen in the following plot and short video, the results were very encouraging.

Made another run with ‘D’ bumped to 0.5 – looks even better.

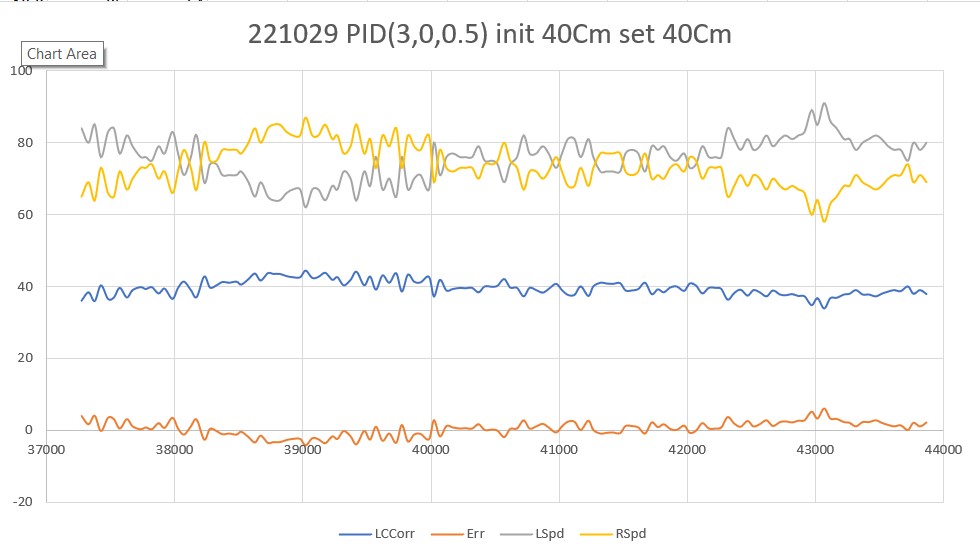
Next, I investigated Wall-E3’s ability to handle wall angle changes. As the following plot and video shows, it actually does quite well with PID(3,0,0.5)

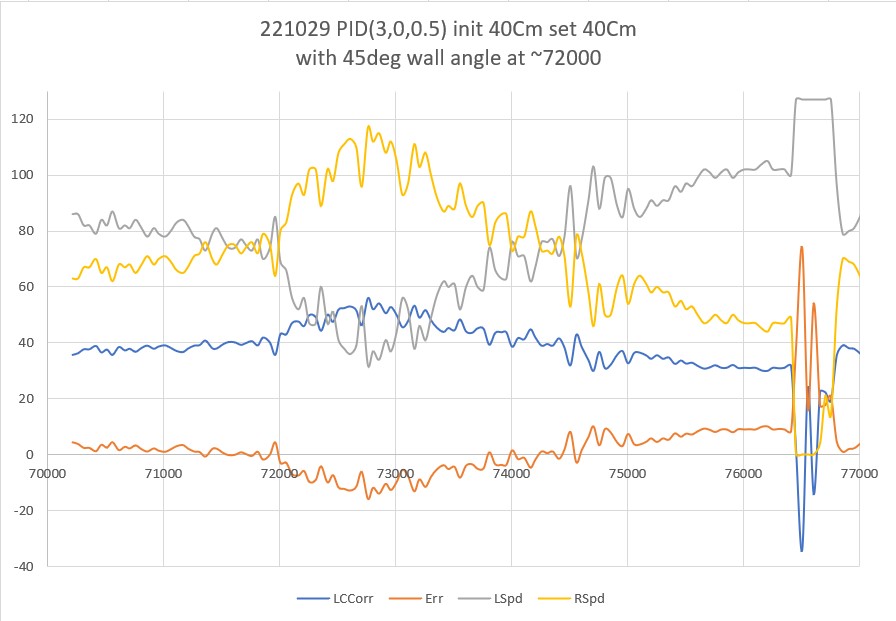
transients at end of run are due to encountering another angled wall – not shown in video

30 October 2022 Update

After a few more trials, I think I ended up with PID(3,0,1) as a reasonable compromise. With this setup, Wall-E3 can navigate both concave and convex wall angle changes, as shown in the following plot and short video.

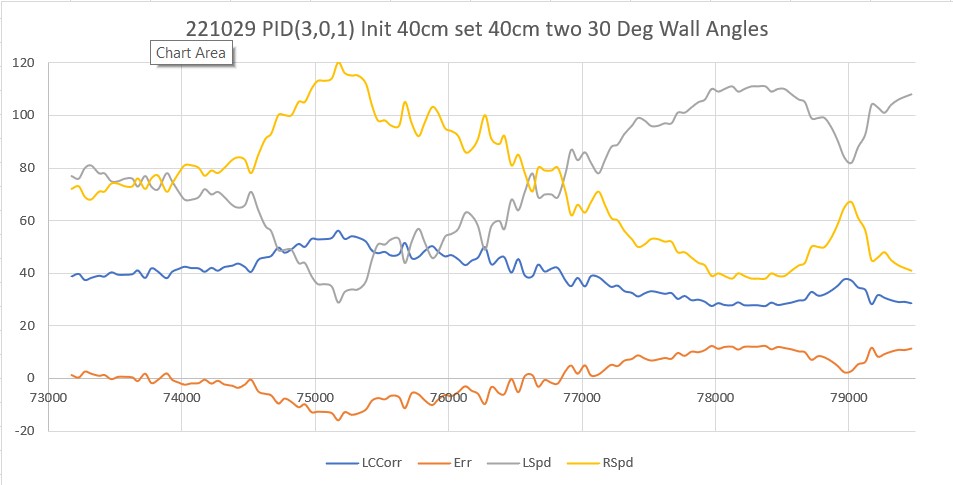
As an aside, I also investigated several other PID triplets of the form (K*3,0,K*1) to see if other values of K besides 1 would produce the same behavior. At first I thought both K = 2 and K = 3 did well, but after a couple of trials I found myself back at K = 1. I’m not sure why there is anything magic about K = 1, but it’s hard to get around the fact that K = 2 and K = 3 did not work as well tracking my ‘sandbox’ walls.

At this point, I think it may be time to back-port the above results into my WallE3_AnomalyRecovery_V2.sln project, and then ultimately back into my main robot control project.

06 November 2022 Update:

Well, now I know why my past efforts at wall tracking didn’t rely exclusively on offset distance as measured by the 3 VL53L0X sensors on each side of the robot. The problem is that the reported distance is only accurate when the robot is parallel to the wall; any off-parallel orientation causes the reported distance to increase, even though the robot body is at the same distance. In the above work I thought I could beat this problem by compensating the distance measurement by the cosine of the off-parallel angle. This works (sort of) but causes the control loop to lag way behind what the robot is actually doing. Moreover, since there can be small variations in the distance reported by the VL53L0X array, the robot can be physically parallel to the wall while the sensors report an off-parallel orientation, or alternatively, the robot can be physically off-parallel (getting closer or farther away) to the wall, while the sensors report that it is parallel and consequently no correction is required. This is why, in previous versions, I tried to incorporate a absolute distance measurement along with orientation information into a single PID loop (didn’t work very well).

09 November 2022 Update:

After beating my head against the problem of tracking the nearby wall using a three-element array of VL53L0X distance sensors and a PID algorithm, I finally decided it just wasn’t wasn’t working well enough to rely on for generalized wall tracking. It does work, but has a pretty horrendous failure mode. If the robot ever gets past about 45 deg orientation w/r/t the near wall, the distance values from the VL53L0X sensor become invalid and the robot goes crazy.

So, I have been spending my night-time sleep preparation time (where I do some of my best thinking) trying to think of different ways of skinning this particular cat, as follows:

  • The robot needs to be able to accurately track a given offset
  • Must have enough agility to accommodate abrupt wall direction changes (90 deg changes are easy – but there are several 45 deg changes in our house)
  • Must handle obstacles appropriately.

It’s that first item on the list that I can’t seem to handle with the typical PID algorithm. So, I started to think about alternative schemes, and the one I decided to experiment with was the idea of implementing a zig-zag tracking algorithm using my already-proven SpinTurn() function. SpinTurn() uses relative heading output from my MP6050 MPU to implement CW/CCW turns, and has proven to be quite reliable (after Homer Creutz and I beat MPU6050 FIFO management into submission).

I modified one of my Wall Track Tuning programs to implement the ‘zig-zag’ algorithm, and ran some tests in my office ‘sandbox’. As the following Excel plot and short video shows, it actually did quite well, considering it was the product of a semi-dream state thought process!

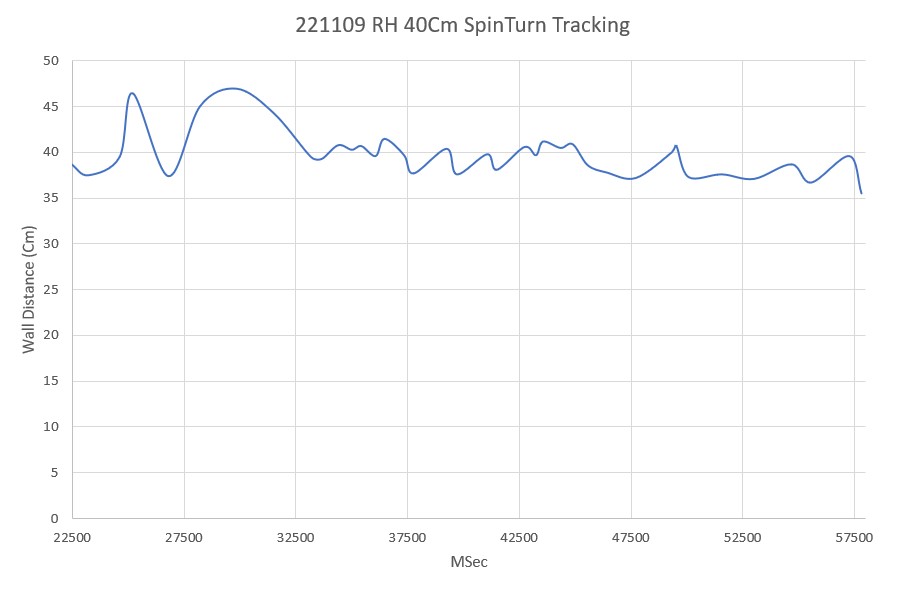
As can be seen from the above, the robot did a decent job of tracking the desired 40Cm offset (average distance for the run was 39.75Cm), especially for the first iteration. I should be able to tweak the algorithm to track the wall faster and with less of a ‘drunken sailor’ behavior.

Stay tuned,

Frank

Wall-E3 Replacing Mega 2560 With Teensy 3.5 Part IV

Leave a reply

Posted 14 January 2022

After finding and fixing the connector problem that prevented the IR Homing Teensy 3.2 module from communicating via I2C with the Teensy 3.5 main controller, I was ready to move on to some real IR homing tests.

For this effort, I decided to change the IR homing algorithm over from the PID library to my home-grown PID routine, discussed here. In the process, I realized that my PIDCalcs() function was overly complex; in particular the ‘sampletime’ calling argument is never used inside the function, as a regular interval is assumed. In all my PID implementations, this is a valid assumption, as I use an ‘elapsedMillisec’ object to enforce regular calls to PIDCalcs(). After eliminating this parameter, the PIDCalcs() function now looks like this:

And the calling routine for this round of testing (not using distance information) looks like this:

The ‘steering value’ output from the IR Homing beacon demodulator ranges from -1 to +1, and motor speeds range from 0 to 255 with a median value of 127. So, I started testing WALL-E3 with a PID of 100,0,0 – the idea being that a max output of +/- 1 from the demodulator would produce an output of +/- 100, which, when used to modulate motor speeds from the median value of 127 would produce motor speeds of 227/27 in one direction and 27/227 in the other. In other words, a Kp value of 100 should produce significant motor speed modulation without hitting the motor speed limits in either direction.

I set up a small test range in my office, and made a couple of runs. Here’s a short video showing on of the runs, and an Excel plot showing steering value and motor speeds vs time.

Homing beacon on the carpet patch. Note smooth turning behavior at start due to new wheel geometry

The next step is to increase the Kp value to the point where oscillations occur, as the starting point for the Zeigler-Nichols PID tuning method. For PID = (200,0,0) I got this behavior.

And for PID = (250,0,0),

And Kp = 300

Looks like Kp = 300 might be a good place to start. So, according to the Zeigler-Nichols PID tuning method, I should use Kp = 0.5Kc = 150, Ki = 0.45Kc = 135, Kd = 0.6Kc = 180. Using these values, I get:

Needless to say, this is NOT what I had in mind! Clearly I erred somewhere along the way. Abandoning the Z-N tuning algorithm, I turned to the ‘manual’ tuning procedure I have used in the past (also discussed in the Z-N article): With Ki, Kd set to 0, increase Kp until the system oscillates, but before it becomes unstable. Then increase Ki until the oscillations stop. Then increase D until “the system achieves an acceptable quick loop to its set-point” (whatever that means).

Starting with a Kd of 200, I increased Ki in increments of 50 to get:

This looks pretty good, even as a first try. However, when compared to the original PID = (200,0,0) plot (shown below), it looks like the Ki value of 50 didn’t actually do very much one way or the other.

Increasing Ki to 100 produces the following plot.

Not much, if any, improvement. Keeping Kp = 200 and Ki = 100, try increasing Kd in increments of 25. The first increment (Kd = 25) produced a significant change, as shown below:

Which leads me to believe the 25 increment is way too much. Trying 10, we get:

PID = 200,100,10 is much nicer than the Kd = 25 version, but there was an annoying little ‘jag’ off-course right at the end – don’t know why. Just for grins I tried PID = (150,100,10):

And this looks pretty good, actually. I think I may run with these values for a while and see how it works. Here’s the video of the above run:

One final note before leaving this subject. I added some code to IRHomeToChgStnNoPings() to measure the time required to run through each motor speed determination loop. The code simply turns ON a digital output at the start, and turns it OFF again at the end. The loop runs every 200 mSec (the current value of MSEC_PER_IR_HOMING_ADJ), but the time required to do everything is only about 1.5 mSec. In other words, the Teensy sits idle for about 99% of the time while homing to the charging station. Or to put it another way, I could run the loop 10 times faster (20mSec vs 200mSec) and the Teensy wouldn’t even break a sweat!

Stay tuned,

Frank

Turn Rate PID Tuning, Part IV

1 Reply

Posted 10 June 2021,

In my last post on this issue, I described using a small test program to explore an in-line version of the PID (Proportional-Integral-Differential) algorithm for turn rate control with Wall-E2, my autonomous wall-following robot. This post describes some follow-on work on this same subject.

The fundamental problem with all the available Arduino PID libraries is they all require the user to wait in a loop for the PID::Compute() function to decide when to actually produce a new output value, and since this computation is inside the function, it is difficult or impossible to synchronize any other related timed element with the PID function. In my case where I want to control the turn rate of a robot, the input to the PID engine is, obviously, the turn rate, in degrees/sec. But, calculation of the turn rate is necessarily a timed function, i.e. (curent_heading – last_heading) / elapsed_time, where the ‘elapsed_time’ parameter is usually a constant. But, all the Arduino PID libraries use an internal private class member that defines the measurement period (in milliseconds), and this value isn’t available externally (well, it is, but only because the user can set the sample time – it can’t be read). So, the best one can do with the current libraries is to use the same constant for PID::SetSampleTime() and for any external time-based calculations, and hope there aren’t any synchronization issues. With this setup, it would be quite possible (and inevitable IMHO) for the PID::Compute() function to skip a step, or to be ‘phase-locked’ to producing an output that is one time constant off from the input.

The solution to this problem is to not use a PID library at all, and instead place the PID algorithm in-line with the rest of the code. This ensures that the PID calculation any related time-based calculations are operating on the same schedule. The downside of this arrangement is loss of generality; all the cool enhancements described by Brett Beauregard in his wonderful PID tutorial go away or have to be implemented in-line as well. From Brett’s tutorial, here’s ‘the beginner’s PID algorithm’:

The difficulty with all the current PID libraries is the ‘dt’ parameter in the above expression; the implementation becomes much easier if ‘dt’ is a constant – i.e. the time between calculations is a constant. However, this constraint also requires that the library, not the user program, controls the timing. This just doesn’t work when the ‘Input’ parameter above also requires a constant time interval for calculation. In my case of turn rate control, the turn rate calculation requires knowledge of the time interval between calculations, and the calculation itself should be done immediately after the turn rate is determined, using the same time interval. So, the turn rate is calculated and then PID::Compute() is called, but Compute() may or may not generate a new output value, because it can return without action if it’s internal time duration criteria isn’t met; see the problem? It may, or even might, generate a new output value each time, but there is no way to ensure that it will!

After figuring this out the hard way (by trying and failing to make the library work), I finally decided to forget the library – at least for my turn rate problem, and in-line all the needed code. Once I had it all running, I abstracted just the PID algorithm to its own function so I could use it elsewhere. This function is shown below:

As you can see, the explanatory comments are much bigger than the function itself, which is really just eight lines long. Also, it has a huge number of arguments, five of which are references that are updated by the function. This function wouldn’t win any awards for good design, as it has too many arguments (wide coupling), but it does have high cohesion (does just one thing), and the coupling is at least ‘data’ coupling only.

Once this function was implemented, the calling function (in this case ‘SpinTurn()’ looks like this:

In the above code, the lines dealing with ‘TIMSK5’ are there to disable and then re-enable the TIMER5 interrupt I have set up to update external sensor values every 100 mSec. I’m not really sure that this HAS to be done, but once I learned how to do it I figured it wouldn’t hurt, either ☺

Now that I have this ‘PIDCalcs()’ function working properly, I plan to use it in several other places where I currently use the PID library; it’s just so much simpler now, and because all the relevant parameters are visible to the calling program, debugging is now a piece of cake where before it was just an opaque black box.

12 June 2021 Update:

After chasing down and eliminating a number of bugs and edge-case issues, I think I now have a pretty stable/working version of the ‘SpinTurn’ function, as shown below:

With this code in place, I made some 180º turns at 45 & 90 deg/sec, both on my benchtop and on carpet, as shown in the plots and video below:

Average turn rate = 41.8 deg/sec
Average turn rate = 86 deg/sec
Average turn rate = 44.8 deg/sec
Average turn rate = 90.1 deg/sec

Stay Tuned!

Frank

Turn Rate PID Tuning, Part III

1 Reply

In my previous post on this subject, I described my efforts to control the turn rate (in deg/sec) of my two-wheel robot, in preparation for doing the same thing on Wall-E2, four wheel drive autonomous wall following robot.

As noted previously, I have a TIMER5 Interrupt Service Routine (ISR) set up on my four wheel robot to provide updates to the various sensor values every 100 mSec, but was unable to figure out a robust way of synchronizing the PID library’s Compute() timing with the ISR timing. So, I decided to bag the PID library entirely, at least for turn rate control, and insert the PID algorithm directly into the turn rate control, and removing the extraneous stuff that caused divide-by-zero errors when the setSampleTime() function was modified to accept a zero value.

To facilitate more rapid test cycles, I created a new program that contained just enough code to initialize and read the MP6050 IMU module, and a routine called ‘SpinTurnForever() that accepts PID parameters and causes the robot to ‘spin’ turn forever (or at least until I stop it with a keyboard command. Here’s the entire program.

This program includes a function called ‘CheckForUserInput()’ that, curiously enough, monitors the serial port for user input, and uses a ‘switch’ statement to execute different commands. One of these commands (‘q’ or ‘Q’) causes ‘SpinTurnForever()’ to execute, which in turn accepts a 4-paremeter input that specifies the three PID parameters plus the desired turn rage, in deg/sec. This routine then starts and manages a CCW turn ‘forever’, in the ‘while()’ block shown below:

This routine mimics the PID library computations without suffering from library’s synchronization problems, and also allows me to fully instrument the contribution of each PID term to the output. This program also allows me to vary the computational interval independently of the rest of the program, bounded only by the ability of the MPU6050 to produce reliable readings.

After a number of trials, I started getting some reasonable results on my benchtop (hard surface with a thin electrostatic mat), as shown below:

Average turn rate = 89.6 deg/sec

As can be seen in the above plot, the turn rate is controlled pretty well around the 90 deg/sec turn rate, with an average turn rate of 89.6 deg/sec.

The plot below shows the same parameter set, but run on carpet rather than my bench.

Average turn rate = 88.2 deg/sec

Comparing these two plots it is obvious that a lot more motor current is required to make the robot turn on carpet, due to the much higher sideways friction on the wheels.

The next step was to see if the PID parameters for 90 deg/sec would also handle different turn rates. Here are the plots for 45 deg/sec on my benchtop and on carpet:

Average turn rate = 44.7 deg/sec
Average turn rate = 43.8 deg/sec

And then 30 deg/sec on benchtop and carpet

Average turn rate = 29.8 deg/sec
Average turn rate 28.8 deg/sec

It is clear from the above plots that the PID values (5,0.8,0.1) do fairly well for the four wheel robot, both on hard surfaces and carpet.

Having this kind of control over turn rate is pretty nice. I might even be able to do turns by setting the turn rate appropriately and just timing the turn, or even vary the turn rate during the turn. For a long turn (say 180 deg) I could do the first 90-120 at 90 deg/sec, and then do the last 90-60 at 30 deg/sec; might make for a much more precise turn.

All of the above tests were done with a 20 mSec time interval, which is 5x smaller than the current 100mSec time interval used for the master timer in Wall-E2. So, my next set of tests will keep the turn rate constant and slowly increase the time interval to see if I can get back to 100 mSec without any major sacrifice in performance.

28 May 2021 Update:

I went back through the tests using a 100 mSec interval instead of 20 mSec, and was gratified to see that there was very little degradation in performance. The turn performance was a bit more ‘jerky’ than with a 20 mSec interval, but still quite acceptable, and very well controlled, both on the benchtop and carpet surfaces – Yay! Here are some plots to show the performance.

Average turn rate = 29.7 deg/sec
Average turn rate = 28.4 deg/sec
Average turn rate = 44.4 deg/sec
Average turn rate = 43.0 deg/sec
Average turn rate = 89.7 deg/sec
Average turn rate = 86.6 deg/sec

31 May 2021 Update:

I made some additional runs on benchtop and carpet, thinking I might be able to reduce the turn-rate oscillations a bit. I found that by reducing the time interval back to 20 mSec and increase the ‘D’ (differential) parameter. After some tweaking back and forth, I wound up with a PID set of (5, 0.8, 3). Using these parameters, I got the following performance plots.

Average turn rate = 87.3 deg/sec
PID = (5,0.8,3), 20mSec interval, 90 deg/sec

As can be seen in the Excel plot and the movie, the turn performance is much smoother – yay!

Stay tuned!

Frank

Turn Rate PID Tuning, Part II

1 Reply

Posted 14 May 2021,

In my previous post on this topic, I described my efforts to use the Arduino PID library to manage turns with Wall-E2, my autonomous wall following robot. This post talks about a problem I encountered with the PID library when used in a system that uses an external timing source, like the TIMER5 ISR in my system and a PID input that depends on accurate timing, such as my turn-rate input.

In my autonomous wall-following robot project, I use TIMER5 on the Arduino Mega 2560 to generate an interrupt ever 100 mSec, and update all time-sensitive parameters in the ISR. These include results from all seven VL53L0X ToF distance sensors, the front-mounted LIDAR, and heading information from a MP6050 IMU. This simplifies the software immensely, as now the latest information is available throughout the code, and encapsulates all sensor-related calls to a single routine.

In my initial efforts at turn-rate tuning using the Arduino PID library, I computed the turn rate in the ISR by simply using

This actually worked because, the ISR frequency and the PID::Compute() frequency were more or less the same. However, since the two time intervals are independent of each other there could be a phase shift, which might drift slowly over time. Also, if either timer interval is changed sometime down the road, the system behavior could change dramatically. I thought I had figured out how to handle this issue by moving the turn-rate computation inside the PID::Compute() function block, as shown below

In a typical PID use case, you see code like the following:

After making the above change, I started getting really weird behavior, and all my efforts at PID tuning failed miserably. After a LOT of troubleshooting and head-scratching, I finally figured out what was happening. In the above code configuration, the PID generates a new output value BEFORE the new turn rate is computed, so the PID is always operating on information that is at least 100mSec old – not a good way to run a railroad!

Some of the PID documentation I researched said (or at least implied) that by setting the PID’s sample time to zero using PID::SetSampleTime(0), that Compute() would actually produce a new output value every time it was called. This meant that I could do something like the following:

Great idea, but it didn’t work! After some more troubleshooting and head-scratching, I finally realized that the PID::SetSampleTime() function specifically disallows a value of zero, as it would cause the ‘D’ term to go to infinity – oops! Here’s the relevant code

As can be seen from the above, an argument of zero is simply ignored, and the sample time remains unchanged. When I pointed this out to the developer, he said this was by design, as the ‘ratio’ calculation above would be undefined for an input argument of zero. This is certainly a valid point, but makes it impossible to synch the PID to an external master clock – bummer!

After some more thought, I modified my copy of PID.cpp as follows:

By moving the SampleTime = (unsigned long)NewSampleTime; line out of the ‘if’ block, I can now set the sample time to zero without causing problems with the value of ‘ratio’. Now PID::Compute() will generate a new output value every time it is called, which synchs the PID engine with the program’s master timing source – yay!

I tried out a slightly modified version of this technique on my small 2-wheel robot. The two-wheeler uses an Arduino Uno instead of a Mega, so I didn’t use a TIMER interrupt. Instead I used the ‘elapsedMillisecond’ library and set up an elapsed time of 100 mSec, and also modified the program to turn indefinitely at the desired turn rate in deg/sec.

I experimented with two different methods for controlling the turn rate – a ‘PWM’ method where the wheel motors are pulsed at full speed for a variable pulse width, and a ‘direct’ method where the wheel motor speeds are varied directly to achieve the desired turn rate. I thought the PWM method might work better on a heavier robot for smaller angle turns as there is quite a bit of inertia to overcome, but the ‘direct’ method might be more accurate.

Here’s the code for the ‘direct’ method, where the wheel speeds are varied with

Here’s the code for the PWM method: the only difference is that is the duration of the pulse that is varied, not the wheel speed.

Here’s a short video showing the two-wheel robot doing a spin turn using the PWM technique with a desired turn rate of 90 deg/sec, using PID = (1,0.5,0).

The average turn rate for the entire run was about 85 deg/sec.

Here’s another run, this time on carpet:

Average turn rate for the entire run was about 85 deg/sec

Here’s some data from the ‘direct’ method, on hard flooring

Average turn rate was ~ 85 deg/sec

And on carpet

Average turn rate ~83 deg/sec

So, it appears that either the PWM or ‘direct’ methods are effective in controlling the turn rate, and I don’t really see any huge difference between them. I guess the PWM method might be a little more effective with the 4-wheel robot caused by the wheels having to slide sideways while turning.

Stay Tuned!

Frank

Wall Parallel Find PID Tuning

1 Reply

Posted 10 April 2021

In addition to using PID for homing to its charging station and for turn rate control, Wall-E2 also uses PID for finding the parallel orientation to a nearby wall. After successfully tuning the turn rate and IR Homing PID controllers using the Ziegler-Nichols method for PID tuning, I decided to see what I could do with the PID controller for parallel orientation finding

Wall-E2 uses two 3-element VL53L0X Time-of-Flight distance sensors for parallel orientation finding. The idea is that when all three sensors report the same distance, then the robot must be oriented parallel to the wall. The Teensy 3.5 Array Controller MCU calculates a ‘steering value’ using the expression (shown for the left side array):

This value is fed to the PID engine, which drives the motors to zero it out – thus arriving at a parallel orientation. Originally I just basically ‘winged it’ in choosing PID Kp, Ki & Kd values, arriving emperically at Kp = 200, Ki = 50, Kd = 0. However, after going through the K-N process with Wall-E2’s other two PID control setups, I decided to try it with this one as well.

The first step is to determine Kc, the Kp value for which the system oscillates in a reasonably stable fashion. To accomplish this I started with Kp = 20 and worked my way up in stages, plotting the ‘steering value’ each time. The last three trials (as shown in the following plots) were for Kp = 400, Kp = 500 and Kp = 600:

Looking at the above plots, it looks like Kp = 600 will work for Kc. Using the K-N formula, we get

Using the above values for the Parallel Find PID, we get the following plot:

Which is not exactly what I thought it would be – it looks like my guess for Kc must be off. Trying again with a Kc = 400 –> PID = 200,180,240, we get:

which, to my eye at least, seems a bit better.

To test how this worked with ‘real’ parallel finding, I incorporated these parameter values into my ‘RotateToParallelOrientation()’ routine and ran a couple of tests. Here’s one where Wall-E2 starts in the ‘toed-out’ position:

And here’s the Excel plot from this same run

As can be seen, the robot takes less than two seconds to converge on a pretty decent parallel orientation, starting from a 30-40º angle to the near wall.

Here’s another run where the robot starts in the ‘toed-in’ orientation.

And here’s the Excel plot for the run

Again, the robot gets to a pretty decent parallel orientation within 2 seconds of the start of the run. The only concern I have with this run is that it winds up pretty close to the wall.

Turn Rate PID Tuning

1 Reply

Posted 05 April 2021

Wall-E2, my autonomous wall-following robot, does a lot of turns to follow walls. Originally Wall-E2 used a simple timing algorithm to make turns, but this wasn’t very accurate. On a hard surface a 5-second turn at half motor speed could result in a 360º turn, while the same 5 seconds on carpet my only cover 90º. After installing the MPU6050 IMU about 18 months ago, turns could be controlled much more accurately, but the turn rate still varied widely on carpet vs hard flooring. Some time ago, I revised Wall-E2’s program to use a PID engine for turn rate control, but this resulted in a low-frequency ‘motorboating’ movement as the robot ramped up motor current until the angle started changing, followed by ramping the motor current down again because the turn rate target had been exceeded.

After having some success with improving the robot’s performance in homing to the charging station by utilizing the Zeigler-Nichols tuning method, I decided to try using it to improve turn rate control.

The method starts with setting the PID variables to (Kp, 0, 0) and then varying the Kp values to determine Kc, the value at which the setpoint variable (in this case, the turn rate in deg/sec) exhibits a steady oscillation. The value of Kc is then used to calculate all three PID parameters using

The existing setting for Kp, Ki, and Kd was Kp = 5, Ki = 0, Kd = 10, and this resulted in the following plot for a single 270º turn.

To start the process of determining Kc, I first zeroed out the Kd factor, resulting in the following plot:

So the system is clearly exhibiting a ‘constant amplitude oscillation’, but Kc is the minimum Kp value that produces oscillation. So, I started reducing Kp looking for the point at which the oscillation stopped, producing the following plots:

Comparing the above plots, it seems the value of Kc is probably around 0.1. Using the Z-N formula above, I get

These values are almost two orders of magnitude smaller than the values I had been using – ouch! Looking back on the original work, I had declared the Kp, Ki, & Kd variables as ‘const int’, which means the lowest positive value I could use was ‘1’, which might explain why I never tried anything smaller. Of course, I could have also done what I did with the home-to-charger PID engine and arranged the turn rate calculation so that instead of Kc = 0.1, it would have been more like 100, resulting in (Kp,Ki,Kd) values of (50,45,60).

Anyway, using values of (0.05, 0.045, 0.06) results in the following plot

And here is a short video showing the robot executing the 270º turn plotted above

I was quite impressed by the difference between what I had before and the current performance after implementing the Z-N tuning method; the turn rate was an almost constant 40º/sec (an average of 42.9º according to Excel). And, now that I have a semi-constant rate to look at, it appears to me that I should probably crank up the turn rate to something more like 90º/sec.

With the turn rate cranked up to 90º/sec and using the same values for Kp, Ki, Kd, I get the following plot and video.

The plot of turn rate vs time shows considerably more variation with a 90º/sec turn rate, as compared to 45º/sec; maybe Kc is different due to the different physical dynamics of the robot? The average turn rate from the Excel data is 80º/sec; not the 90º/sec I was looking for, but still not bad. Even so, this result is much better than I had before, with extreme motorboating between 0º/sec and something much higher. I may or may not try to re-determine Kc, but in the meantime I think I’ll run with this for a while.

10 April 2021 Update:

Some of the above data were collected at a pretty low charge level. When I had the opportunity to recharge Wall-E2 I re-took the 90º/sec run with the following results:

As the above plot shows, the turn rate was held almost constant (average of 87.9º) throughout the turn – very nice!

Here’s another run, this time on carpet with a fully charged battery. As expected, the robot has a harder time getting started on carpet due to the added sideways friction on the wheels. However, once the turn gets started, it stabilizes fairly well on the 90º turn rate target

Stay tuned,

Frank

Another Try at Charging Station Homing PID Tuning

Leave a reply

Posted 04 April 2021

Lately I have been working on improving the performance of Wall-E2, my autonomous wall-following robot, when homing in and connecting to it’s charging station. The robot uses the PID (Proportional-Integral-Derivative) library to drive the motors to home in on an IR beacon, and this ‘mostly’ works, but still occasionally hangs up on the lead-in rails. I have made several attempts to get this right (see this post and earlier work), but have never really gotten it zeroed in. After yet another web search for tuning help, I ran across this post dealing with the Ziegler-Nichols method for PID tuning. Basically the method starts by setting the proportional (Kp), integral (Ki) and derivative (Kd) terms to zero, and then slowly increasing the proportional (Kp) term until a ‘stable oscillation condition’ is achieved (Kp = Kc). Then the Ki & Kd terms can be calculated using the following relationships:

Getting to the ‘Kc’ (Kp-critical) value for my setup is a bit more difficult than normal, as the PID engine only operates for a few seconds, from the time the IR homing beacon is detected, to the time the robot actually connects (or doesn’t) to the charging probe. Here’s a short video showing a typical run (Kd = 150 in this case), and an Excel plot of the steering value from the same run.

As can be seen from the above, there really isn’t much of an ‘oscillation’ to go on – there is basically only one full cycle from about 10.5 sec to around 12.0 sec.

Here’s another run, this time with Kd set to 200. As can be seen, this is much more like what I was expecting to see, with several full cycles of oscillation. The amplitude trails off a bit toward the end, but this may have been due to a low battery level – I’ll have to repeat this experiment after getting a full charge into the robot.

Kp = 200, Kd = Ki = 0. Period is approximately 1.3 sec

However, using the above data with Kc = 200, we get

I revised my program to incorporate the Z-N numbers from the above calculations, and this resulted in the homing runs shown below; in the first one, Wall-E2 was oriented directly at the charging station beacon, and the robot’s track was pretty much direct, with no side-side oscillation at all. In the second one I oriented the robot a bit off-axis to excite a more active homing response. In both runs, the LEDs on the rear of the robot show the current relative wheel speed commands – LED’s to the left of center indicate higher wheel speed on the left, and vice versa. In the first run, the LEDs show that there is some oscillation of wheel speed commands, but it is relatively small, leading to an almost serene homing performance. In the second run the initial orientation offset forces the robot to more actively manage the wheel speeds to stay ‘on the beam’.

Stay tuned,

Frank

Back to the future with Wall-E2. Wall-following Part III

2 Replies

Posted 24 March 2019,

In my previous post on this subject, I described some initial wall-following tests using a PID controller, and concluded that I would have to use some sort of two-stage approach/capture arrangement to make things work properly.  In addition, I needed some more ‘field’ (i.e., my hallway) testing to determine the best PID values for wall-following.

I started by causing the distance input to vary in a square wave fashion with an amplitude of about 20cm around the 50cm target value.  The resulting speed variations are shown in the following Excel plot.  This gave me some confidence that the basic PID mechanism was working properly.

Square wave response of PID = 1,0,0

After verifying basic operation, I started field testing with the most basic values possible – PID = 1,0,0:  This resulted in a very slow oscillation, as shown in the following video and Excel plot:

PID = 1,0,0, initial offset = target distance = 50cm

Then I moved on to the PID value I had obtained from previous field testing, i.e. PID = 10,0,0. This resulted in the behavior shown in the following video and Excel plot

PID = 10,0,0, initial offset = target distance = 50cm

For completeness, I also tested the PID = 10,2,0 case, but as can be seen in the following video and Excel plot, this did not appreciably change wall-tracking performance, at least not for the offset = target case.

PID = 10,2,0, initial offset = target distance = 50cm

A comparison of all three PID values is shown in the following Excel plot

Next I tried the PID = 1,0,0 case with an initial offset of 25cm and a target of 50cm, to gauge how the PID algorithm performs with an initially large error term.

PID = 1,0,0, initial offset = 25cm, target distance = 50cm

Back to the future with Wall-E2. Wall-following Part II

Leave a reply

Posted 09 February 2019

A long time ago in a galaxy far, far away, I set up a control algorithm for my autonomous wall-following robot Wall-E2.  After a lot of tuning, I wound up with basically a bang-bang system using a motor speed step function of about 50, where the full range of motor speeds is 0-255.  This works, but as you can see in the following chart & Excel diagram, it’s pretty clunky.  The algorithm is shown below, along with an Excel chart of motor speeds taken during a hallway run, and a video of the run.

for left wall tracking

for right wall tracking

 

Run 1, using homebrew algorithm

Note the row of LEDs on the rear. They display (very roughly) the turn direction and rate.

Since the time I set this up, I started using a PID algorithm for the code that homes the robot in on its charging station using a modulated IR beam, and it seems to work pretty well with a PID value of (Kp,Ki,Kd) = (200,0,0).  I’d like to use the knowledge gained for the IR homing subsystem to make Wall-E2 a bit more sophisticated and smooth during wall-following operations (which, after all, will be what Wall-E2 is doing most of the time).

In past work, I have not bothered to set a fixed distance from the wall being followed; I was just happy that Wall-E2 was following the wall at all, much less at a precise distance. Besides, I really didn’t know if having a preferred distance was a good idea.  However, with the experience gained so far, I now believe a 20-30 cm offset would probably work very well in our home.

So, my plan is to re-purpose the PID object used for IR homing whenever it isn’t actually in the IR homing mode, but with the PID values appropriate for wall-following rather than beam-riding.

PID Parameters:

For the beam-riding application I used a setpoint of zero, meaning the algorithm adjusts the control value (motor speed adjustment value) to drive the input value (offset from IR beam center) to zero.  This works very nicely as can be seen in the videos.  However, for the wall-following application I am going to use a setpoint of about 20-30cm, so that the algorithm will (hopefully) drive the motors to achieve this offset.  The Kp, Ki, & Kd values will be determined by experimentation.

 

 

13 February 2019 Update:

I got the PID controller working with a target offset of 25cm and Kp,Ki,Kd = 2,0,0 and ran some tests in my hallway.  In the first test I started with Wall-E2 approximately 25cm away from the wall. As can be seen in the following video, this worked quite well, and I thought “I’m a genius!”  Then I ran another test with Wall-E2 starting about 50cm away from the wall, and as can be seen in the second video, Wall-E2 promptly dived nose-first right into the wall, and I thought “I’m an idiot!”

 

 

The problem, of course, is the PID algorithm correctly turns Wall-E2 toward the wall to reduce the offset to the target value, but in doing so it changes the orientation of the ping sensor with respect to the wall, and the measured distance goes up instead of down.  The PID response is to turn Wall-E2 more, making the problem even worse, ending with Wall-E3 colliding nose-first with the wall it’s supposed to be following – oops!

So, it appears that I’ll need some sort of two stage approach the the constant-offset wall following problem, with an ‘approach’ stage and a ‘capture’ stage.  If the measured distance is outside a predefined capture window (say +/- 2cm or so), then either the PID algorithm needs to be disabled entirely in favor of a constant-angle approach, or the PID parameters need to change to something more like Kp,Ki,Kd = 0,1,1 or something.  More experimentation required.

Stay tuned,

Frank