Monthly Archives: April 2021

Wall Parallel Find PID Tuning

1 Reply

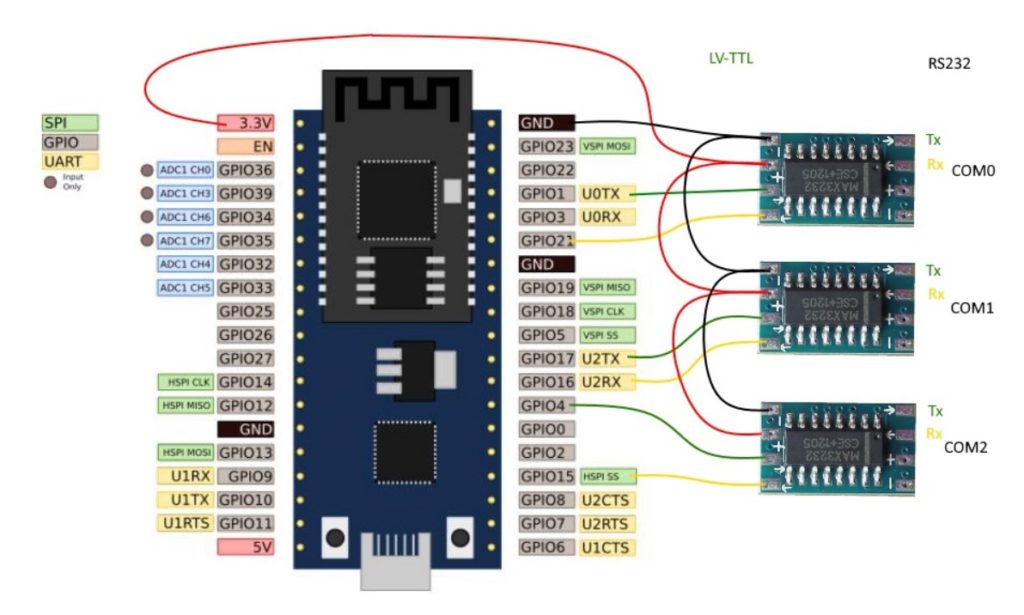
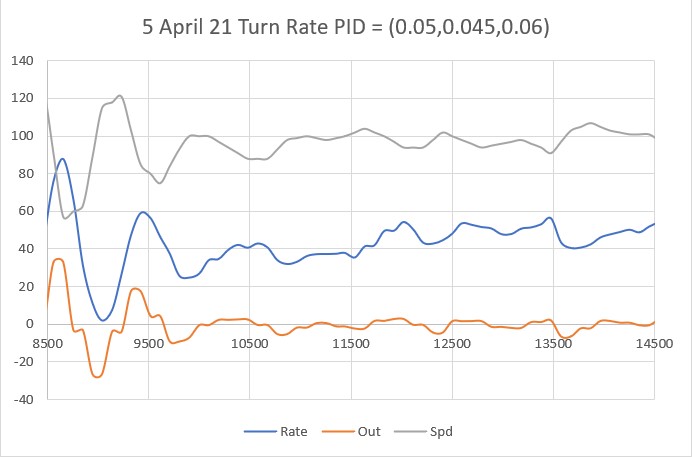
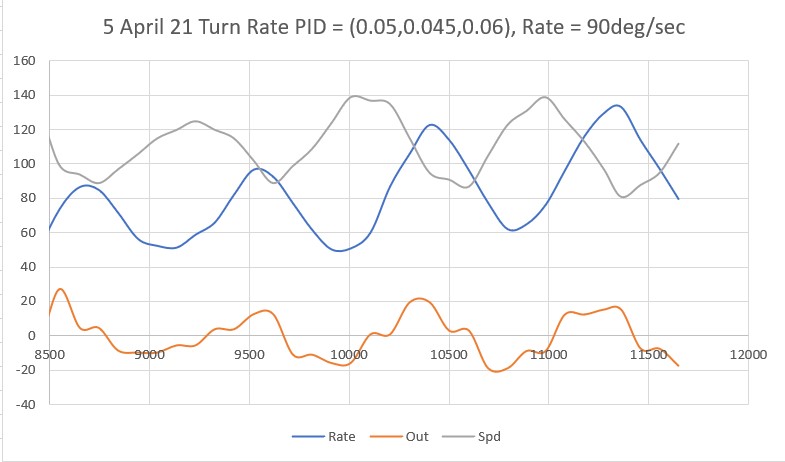
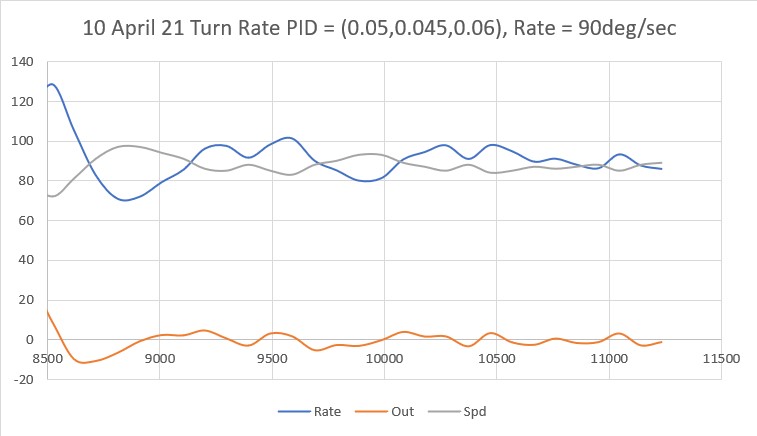
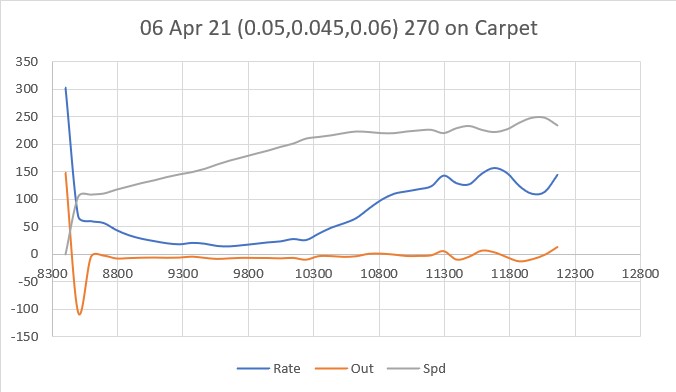
Posted 10 April 2021

In addition to using PID for homing to its charging station and for turn rate control, Wall-E2 also uses PID for finding the parallel orientation to a nearby wall. After successfully tuning the turn rate and IR Homing PID controllers using the Ziegler-Nichols method for PID tuning, I decided to see what I could do with the PID controller for parallel orientation finding

Wall-E2 uses two 3-element VL53L0X Time-of-Flight distance sensors for parallel orientation finding. The idea is that when all three sensors report the same distance, then the robot must be oriented parallel to the wall. The Teensy 3.5 Array Controller MCU calculates a ‘steering value’ using the expression (shown for the left side array):

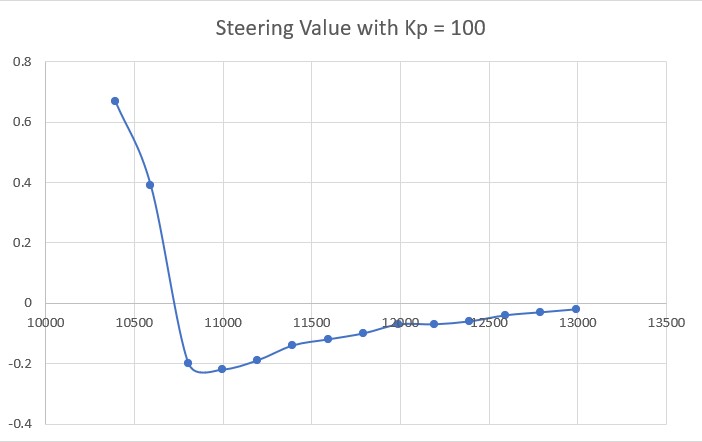
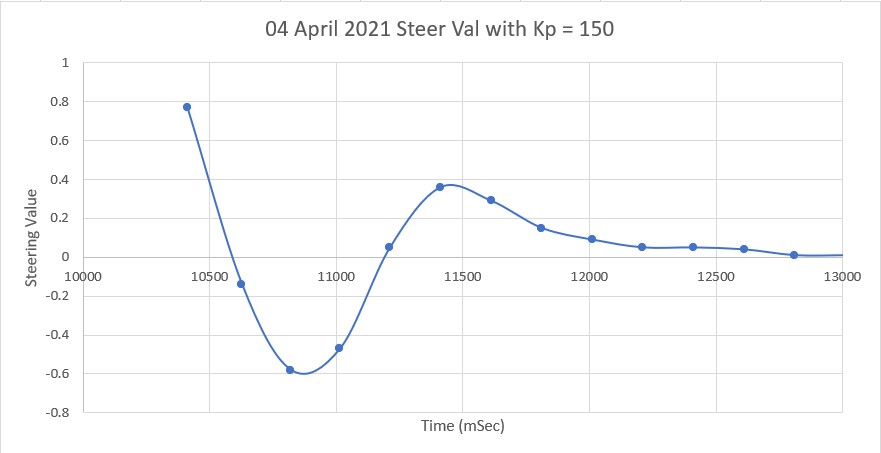
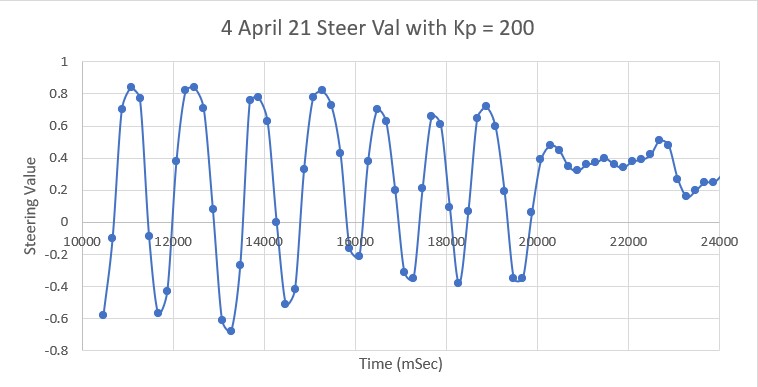
This value is fed to the PID engine, which drives the motors to zero it out – thus arriving at a parallel orientation. Originally I just basically ‘winged it’ in choosing PID Kp, Ki & Kd values, arriving emperically at Kp = 200, Ki = 50, Kd = 0. However, after going through the K-N process with Wall-E2’s other two PID control setups, I decided to try it with this one as well.

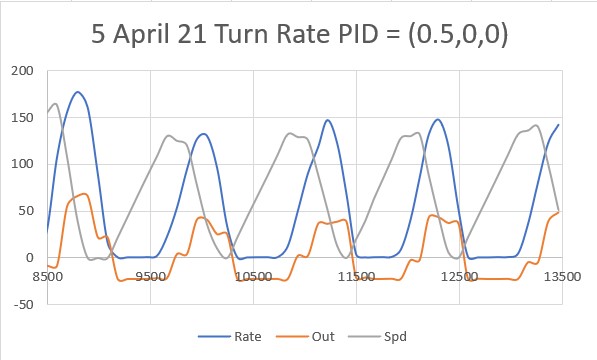
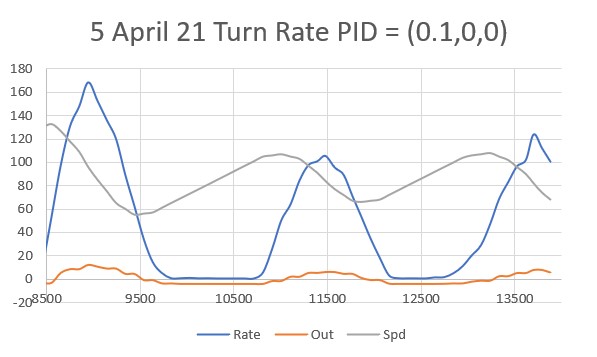
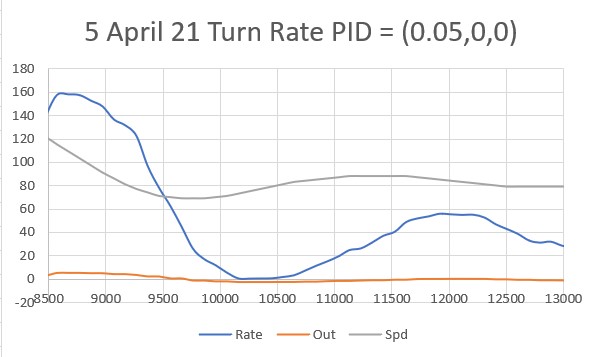
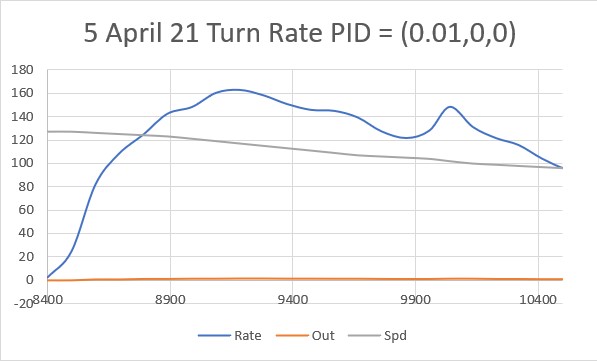
The first step is to determine Kc, the Kp value for which the system oscillates in a reasonably stable fashion. To accomplish this I started with Kp = 20 and worked my way up in stages, plotting the ‘steering value’ each time. The last three trials (as shown in the following plots) were for Kp = 400, Kp = 500 and Kp = 600:

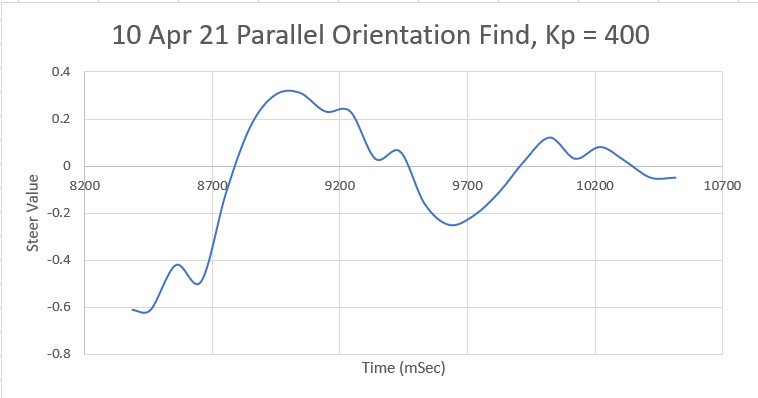
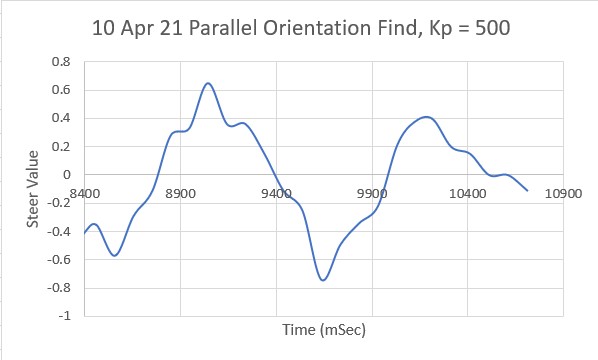
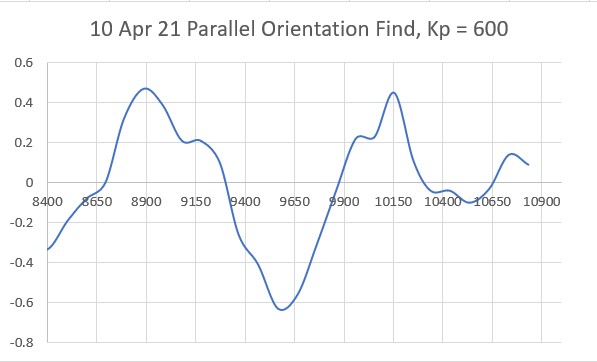
Looking at the above plots, it looks like Kp = 600 will work for Kc. Using the K-N formula, we get

Using the above values for the Parallel Find PID, we get the following plot:

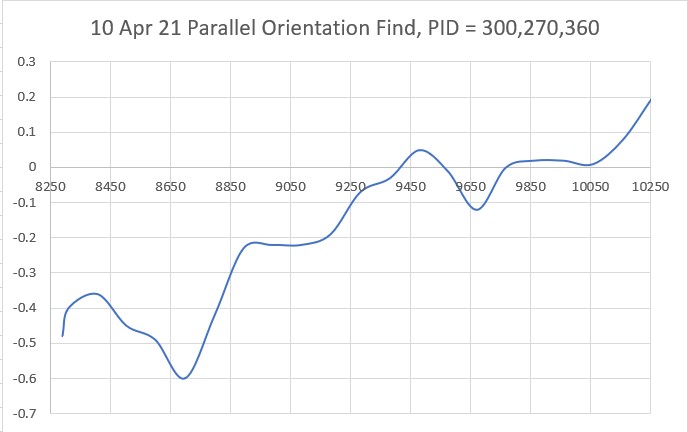
Which is not exactly what I thought it would be – it looks like my guess for Kc must be off. Trying again with a Kc = 400 –> PID = 200,180,240, we get:

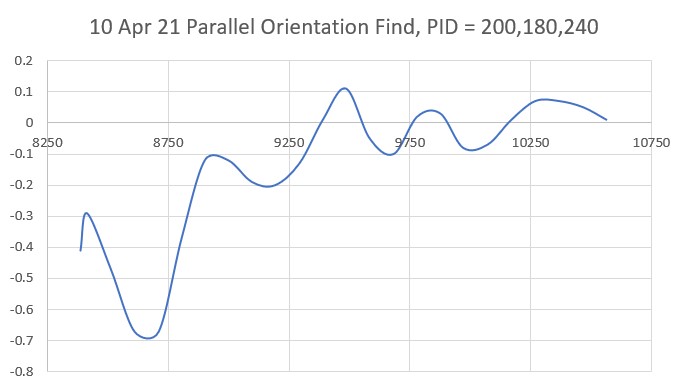
which, to my eye at least, seems a bit better.

To test how this worked with ‘real’ parallel finding, I incorporated these parameter values into my ‘RotateToParallelOrientation()’ routine and ran a couple of tests. Here’s one where Wall-E2 starts in the ‘toed-out’ position:

And here’s the Excel plot from this same run

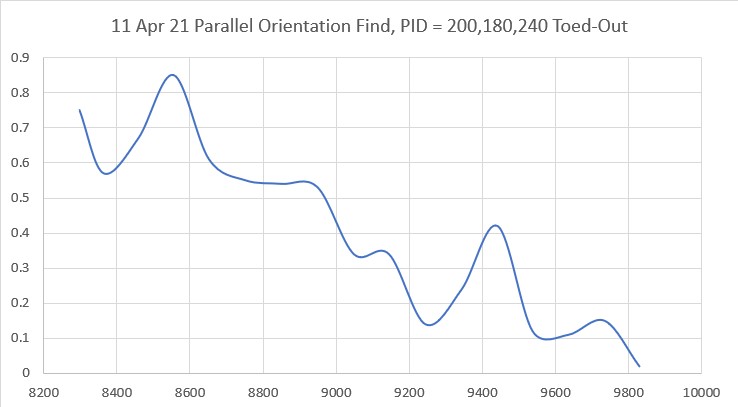
As can be seen, the robot takes less than two seconds to converge on a pretty decent parallel orientation, starting from a 30-40º angle to the near wall.

Here’s another run where the robot starts in the ‘toed-in’ orientation.

And here’s the Excel plot for the run

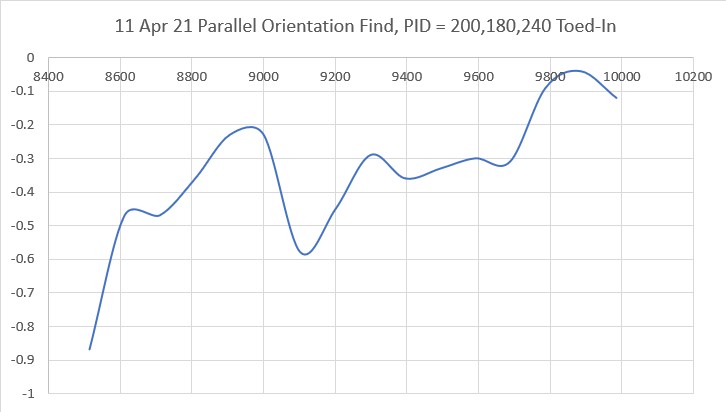
Again, the robot gets to a pretty decent parallel orientation within 2 seconds of the start of the run. The only concern I have with this run is that it winds up pretty close to the wall.

Serial Bridge over WiFi using ESP32 DevKitC

3 Replies

Posted 09 April 2021

I have been wanting to upgrade my robot’s brains from the old Arduino Mega 2560 to a more modern Teensy 3.x or 4.x MCU for some time now, but have been stymied by the lack of Over-The-Air (OTA) programming support. My current Mega-based setup uses a pair of Pololu Wixels to form a transparent wireless bi-directional serial link between my PC and the robot. My Microsoft Visual Studio IDE sees the link as just another COM port, and the Mega thinks it’s Tx/Rx0 lines are connected directly to the PC; couldn’t be simpler and more effective. The range of the Wixel connection is on the order of a few tens of meters, but that’s all I need for managing my autonomous wall-following robot.

Unfortunately, the Teensy world seems a bit short on effective wireless OTA solutions, or at least my searches have come up mostly dry. Some users report they have been able to use a Raspberry Pi Zero-W for this purpose, but that seems like a major overkill

After yet another Google search, I started seeing some posts about the ability to form a wireless serial data bridge using an ESP32 wireless-enabled development module, and I since I happened to have a ESP32 DevKitC hanging around Idecided to try my hand at that, maybe as a first step to achieving OTA nirvana with a Teensy 3/4.x.

The starting point for this project was this tutorial (the bottom ‘Serial Bridge Using ESP8266 (Simpler)’ part), based on this module sold on the AliExpress site. The AliExpress module wasn’t exactly the same as the DevKitC I had on hand, but it was close enough and AFAICT the pinouts are identical.

The first step was getting the Arduino/VS2019 IDE to recognize the ESP32 hardware. This was a semi-major PITA, but I eventually found some posts showing how the board information could be added to the system.

The next step was getting PuTTY downloaded and installed on my Win10 system. This went fairly easily.

Next I downloaded the ESP32 serial bridge software from the GitHub site and set it up as a project in my VS2019/Visual Micro IDE. This all seemed to work, and I was able to upload the program to my DevKitC module

I also happened to have an old CKdevices FTDI module, so I was able to connect to the required serial lines on the ESP32 module. However, I discovered that the tutorial didn’t use the standard Tx/Rx lines shown in the DevKitC pinout diagram; evidently they had to be moved to allow all three UART/USB modules to be connected at the same time. The actual pinouts used by the tutorial are:

After some fumbling around, I finally realized that the ‘GPIOxx’ labels in the above pinout list is the same as the numbers printed on the actual module, i.e. ‘GPIO21′ <==> ’21’ on the module PCB (the lone exception to this is ‘GPIO1’, which corresponds to ‘TX’ on the module). Here’s a picture from the GitHub documentation showing the actual layout expected by the sofware.

After working my way though these problems, here’s the physical setup I wound up with:

CkDevices FTDI UART/USB connected to COM5 on USB side, Tx2/Rx2 on ESP32 side
Detail showing the pin connections to ESP32 module. Yellow is connected to ESP32 Rx2, Green to Tx2

With the above hardware setup, I was able to pass serial data from one PuTTY terminal connected to the 192.168.4.1/8882 port, and another connected to COM5 on the PC (corresponding to COM2 on the ESP32).

Having accomplished this, I’m still unsure how to go about using this capability to program a Teensy 3/4.x using the wireless link. More study required!

Frank

Turn Rate PID Tuning

1 Reply

Posted 05 April 2021

Wall-E2, my autonomous wall-following robot, does a lot of turns to follow walls. Originally Wall-E2 used a simple timing algorithm to make turns, but this wasn’t very accurate. On a hard surface a 5-second turn at half motor speed could result in a 360º turn, while the same 5 seconds on carpet my only cover 90º. After installing the MPU6050 IMU about 18 months ago, turns could be controlled much more accurately, but the turn rate still varied widely on carpet vs hard flooring. Some time ago, I revised Wall-E2’s program to use a PID engine for turn rate control, but this resulted in a low-frequency ‘motorboating’ movement as the robot ramped up motor current until the angle started changing, followed by ramping the motor current down again because the turn rate target had been exceeded.

After having some success with improving the robot’s performance in homing to the charging station by utilizing the Zeigler-Nichols tuning method, I decided to try using it to improve turn rate control.

The method starts with setting the PID variables to (Kp, 0, 0) and then varying the Kp values to determine Kc, the value at which the setpoint variable (in this case, the turn rate in deg/sec) exhibits a steady oscillation. The value of Kc is then used to calculate all three PID parameters using

The existing setting for Kp, Ki, and Kd was Kp = 5, Ki = 0, Kd = 10, and this resulted in the following plot for a single 270º turn.

To start the process of determining Kc, I first zeroed out the Kd factor, resulting in the following plot:

So the system is clearly exhibiting a ‘constant amplitude oscillation’, but Kc is the minimum Kp value that produces oscillation. So, I started reducing Kp looking for the point at which the oscillation stopped, producing the following plots:

Comparing the above plots, it seems the value of Kc is probably around 0.1. Using the Z-N formula above, I get

These values are almost two orders of magnitude smaller than the values I had been using – ouch! Looking back on the original work, I had declared the Kp, Ki, & Kd variables as ‘const int’, which means the lowest positive value I could use was ‘1’, which might explain why I never tried anything smaller. Of course, I could have also done what I did with the home-to-charger PID engine and arranged the turn rate calculation so that instead of Kc = 0.1, it would have been more like 100, resulting in (Kp,Ki,Kd) values of (50,45,60).

Anyway, using values of (0.05, 0.045, 0.06) results in the following plot

And here is a short video showing the robot executing the 270º turn plotted above

I was quite impressed by the difference between what I had before and the current performance after implementing the Z-N tuning method; the turn rate was an almost constant 40º/sec (an average of 42.9º according to Excel). And, now that I have a semi-constant rate to look at, it appears to me that I should probably crank up the turn rate to something more like 90º/sec.

With the turn rate cranked up to 90º/sec and using the same values for Kp, Ki, Kd, I get the following plot and video.

The plot of turn rate vs time shows considerably more variation with a 90º/sec turn rate, as compared to 45º/sec; maybe Kc is different due to the different physical dynamics of the robot? The average turn rate from the Excel data is 80º/sec; not the 90º/sec I was looking for, but still not bad. Even so, this result is much better than I had before, with extreme motorboating between 0º/sec and something much higher. I may or may not try to re-determine Kc, but in the meantime I think I’ll run with this for a while.

10 April 2021 Update:

Some of the above data were collected at a pretty low charge level. When I had the opportunity to recharge Wall-E2 I re-took the 90º/sec run with the following results:

As the above plot shows, the turn rate was held almost constant (average of 87.9º) throughout the turn – very nice!

Here’s another run, this time on carpet with a fully charged battery. As expected, the robot has a harder time getting started on carpet due to the added sideways friction on the wheels. However, once the turn gets started, it stabilizes fairly well on the 90º turn rate target

Stay tuned,

Frank

Another Try at Charging Station Homing PID Tuning

Leave a reply

Posted 04 April 2021

Lately I have been working on improving the performance of Wall-E2, my autonomous wall-following robot, when homing in and connecting to it’s charging station. The robot uses the PID (Proportional-Integral-Derivative) library to drive the motors to home in on an IR beacon, and this ‘mostly’ works, but still occasionally hangs up on the lead-in rails. I have made several attempts to get this right (see this post and earlier work), but have never really gotten it zeroed in. After yet another web search for tuning help, I ran across this post dealing with the Ziegler-Nichols method for PID tuning. Basically the method starts by setting the proportional (Kp), integral (Ki) and derivative (Kd) terms to zero, and then slowly increasing the proportional (Kp) term until a ‘stable oscillation condition’ is achieved (Kp = Kc). Then the Ki & Kd terms can be calculated using the following relationships:

Getting to the ‘Kc’ (Kp-critical) value for my setup is a bit more difficult than normal, as the PID engine only operates for a few seconds, from the time the IR homing beacon is detected, to the time the robot actually connects (or doesn’t) to the charging probe. Here’s a short video showing a typical run (Kd = 150 in this case), and an Excel plot of the steering value from the same run.

As can be seen from the above, there really isn’t much of an ‘oscillation’ to go on – there is basically only one full cycle from about 10.5 sec to around 12.0 sec.

Here’s another run, this time with Kd set to 200. As can be seen, this is much more like what I was expecting to see, with several full cycles of oscillation. The amplitude trails off a bit toward the end, but this may have been due to a low battery level – I’ll have to repeat this experiment after getting a full charge into the robot.

Kp = 200, Kd = Ki = 0. Period is approximately 1.3 sec

However, using the above data with Kc = 200, we get

I revised my program to incorporate the Z-N numbers from the above calculations, and this resulted in the homing runs shown below; in the first one, Wall-E2 was oriented directly at the charging station beacon, and the robot’s track was pretty much direct, with no side-side oscillation at all. In the second one I oriented the robot a bit off-axis to excite a more active homing response. In both runs, the LEDs on the rear of the robot show the current relative wheel speed commands – LED’s to the left of center indicate higher wheel speed on the left, and vice versa. In the first run, the LEDs show that there is some oscillation of wheel speed commands, but it is relatively small, leading to an almost serene homing performance. In the second run the initial orientation offset forces the robot to more actively manage the wheel speeds to stay ‘on the beam’.

Stay tuned,

Frank