Posted 09 June, 2017
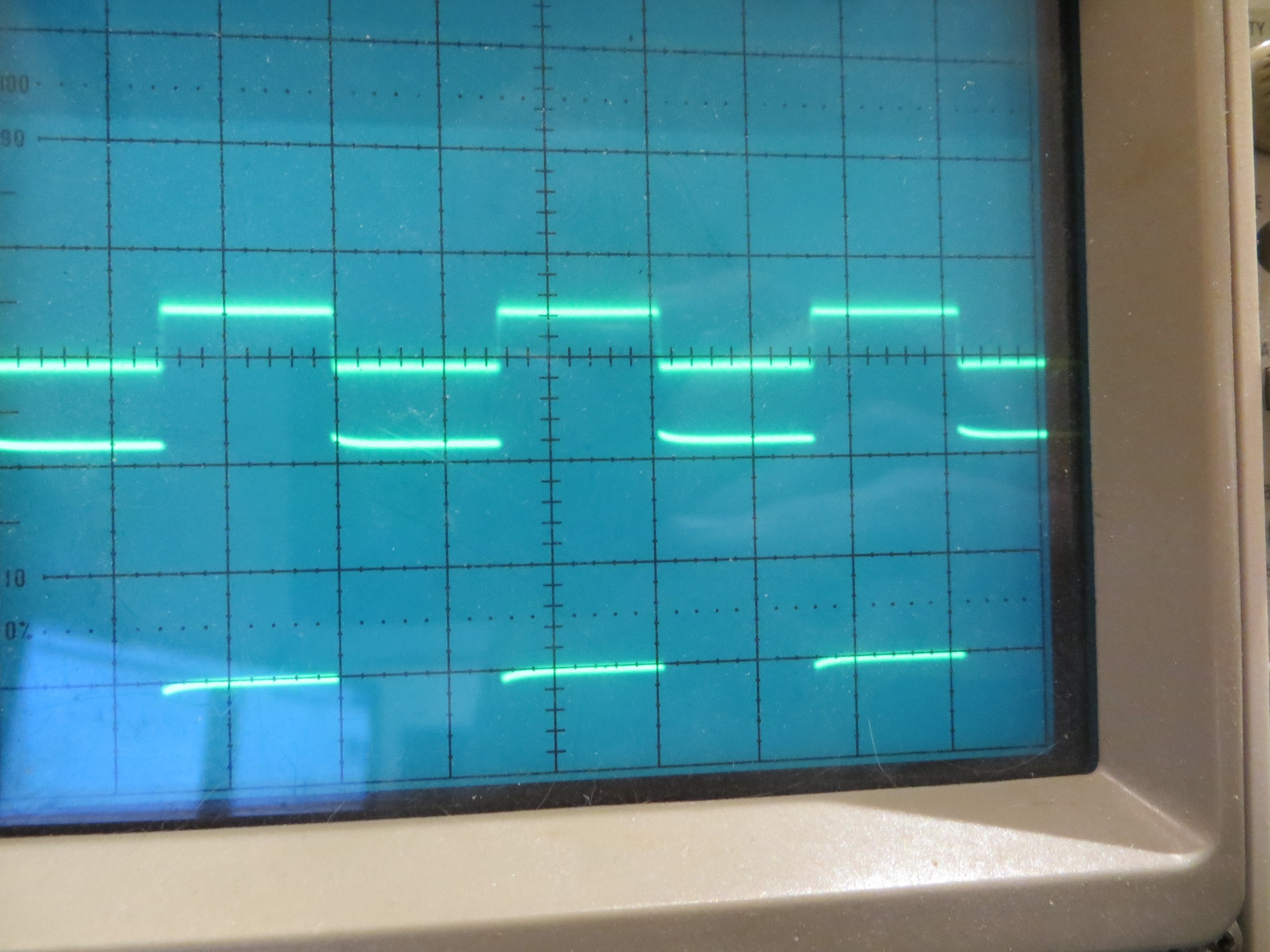
In getting the Arduino code working on my Uno/Trinket test setup (shown below), I have been having some trouble getting the delays right. It finally occurred to me that I should run some basic timing experiments, so here goes:
Sample Group Acquisition Loop:
this is the loop that acquires analog samples from the IR detector, and sums 1/4 cycle’s worth into a single ‘sample group’. To measure this time, I ran the following code:
int startusec = micros();
int sum = 0;
for (int i = 0; i < 1000; i++)
{
int samp = analogRead(SQWAVE_INPUT_PIN1);
sum += samp;
}
int endusec = micros();
Serial.print("time required for 1000 analog read/sum cycles = "); Serial.println(endusec - startusec);
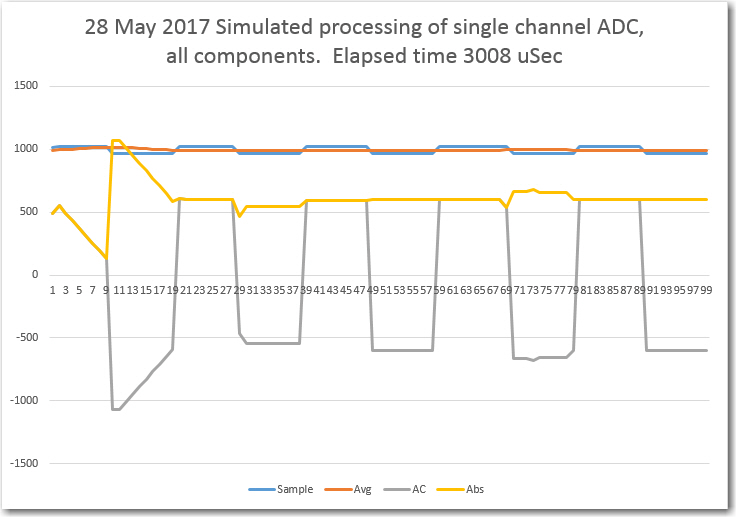
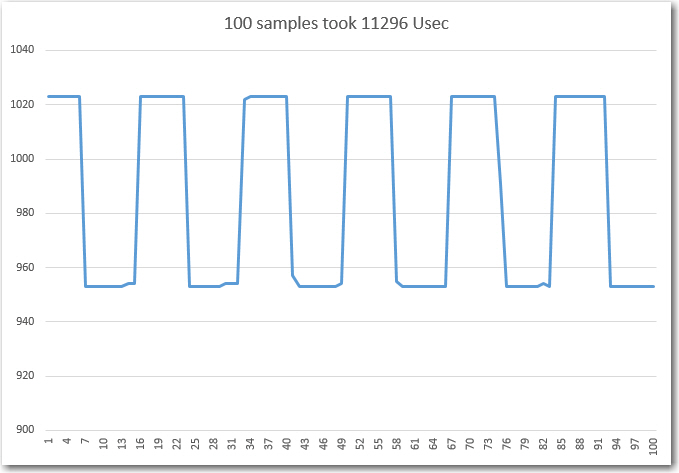
The time required for 1000 cycles was 15064 uSec, meaning that one pass through the loop takes an average of just over 15 uSec. Adding a 85 uSec delay to the loop should result in a loop time of exactly 100 uSec, and a 1000 pass loop time of 100,000 uSec or 0.1sec. The actual result was 99504, or about 99.5 uSec/cycle – pretty close!
Next, I replaced the summation with a write to a 500-element array (couldn’t do 1000 and still fit within the Uno’s 2K memory limit), and verified that this did not materially change the loop timing. The time required for 500 loops was 49788; twice that time would be 99576, or almost exactly the same as the 99504 time for the summation version.
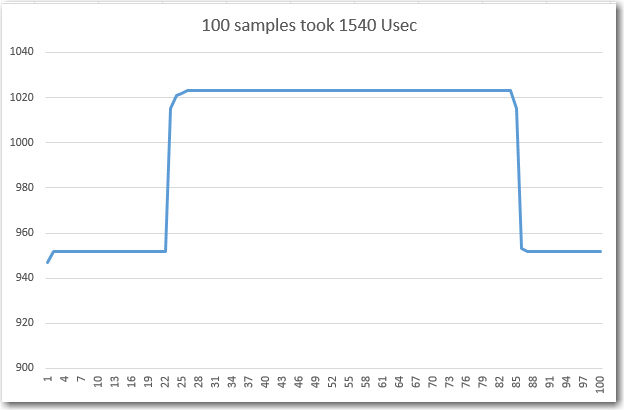
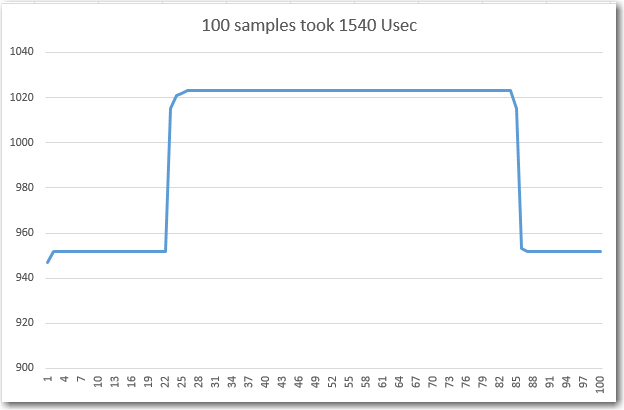
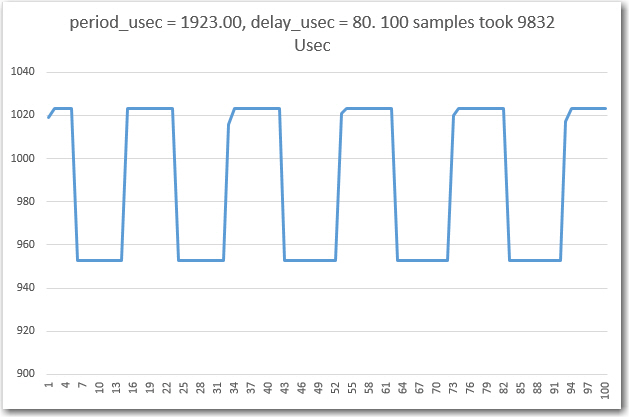
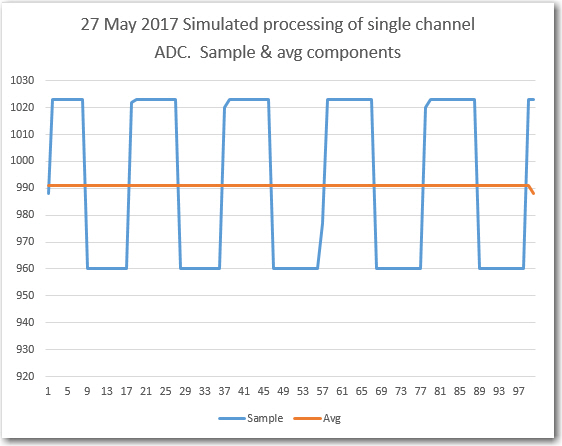
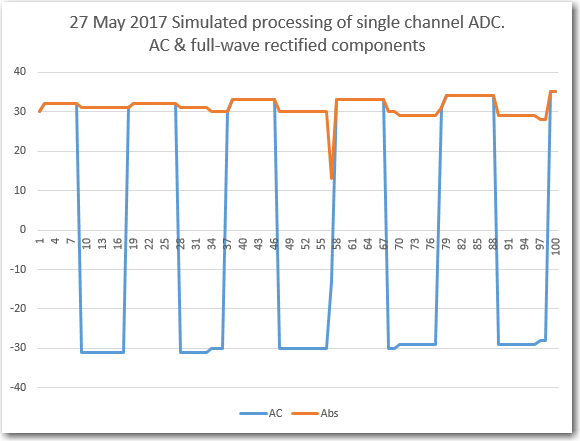
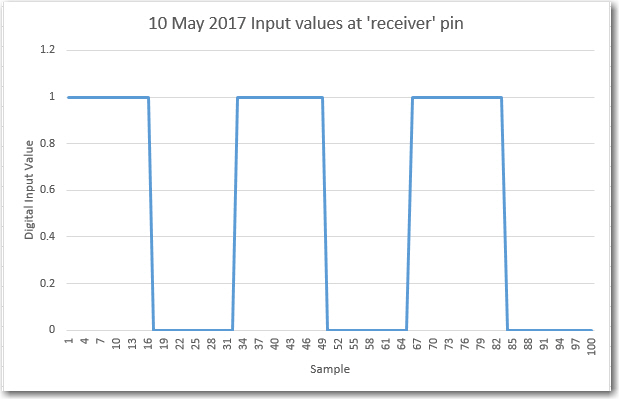
Then I tweaked the delay to achieve as close to 25 complete cycles as possible, as shown in the Excel plot below. With an 82uSec loop delay, the total time for 500 loop iterations was 48272, or about 96.544 uSec per loop iteration.
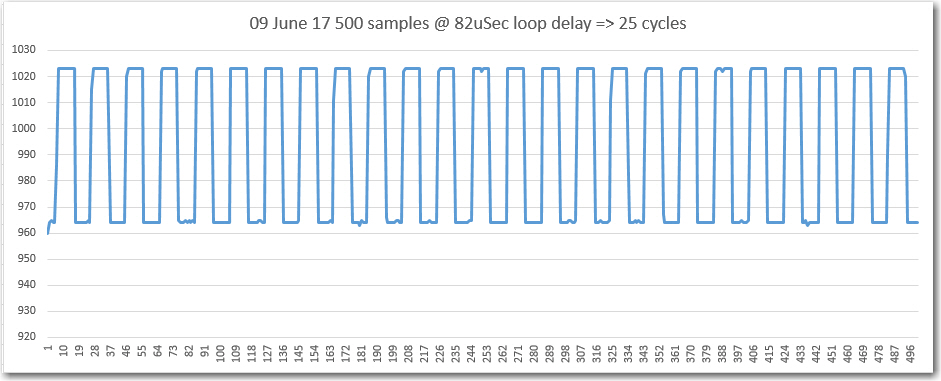
96.544 uSec per loop iteration, and 20 loop iterations per cycle gives 20*96.544 = 1930.88 uSec per cycle or 518 Hz. This is very close to the 525Hz value I got from my O’scope frequency readout when I first fabricated my little test setup.
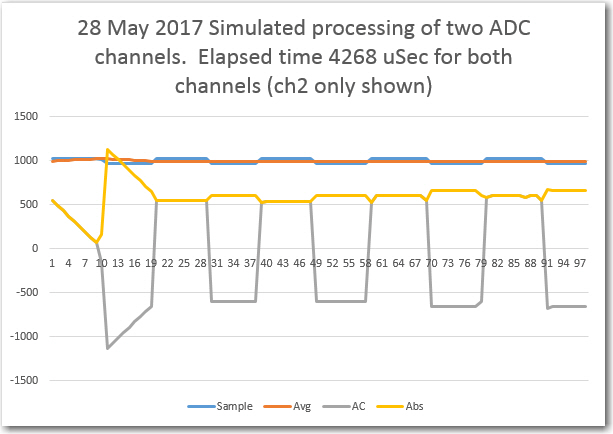
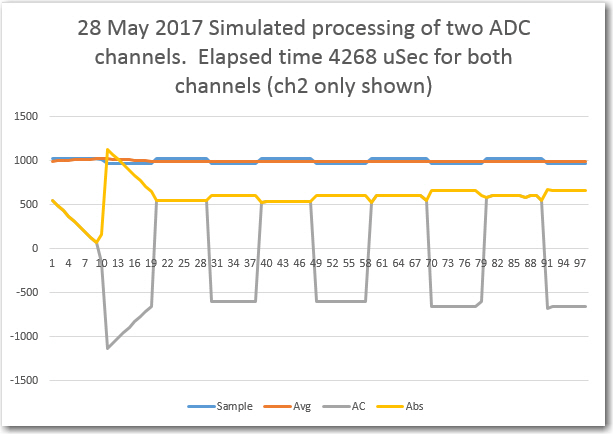
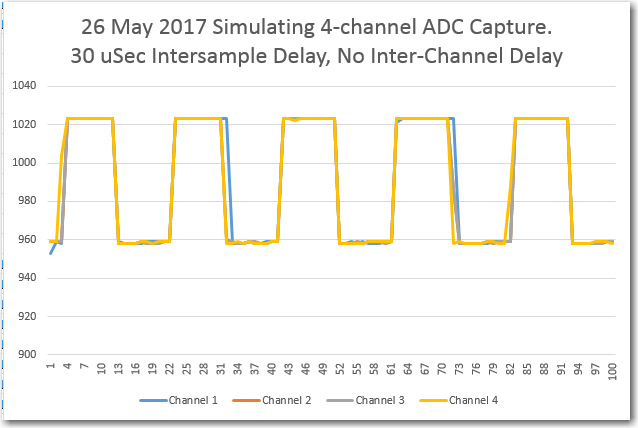
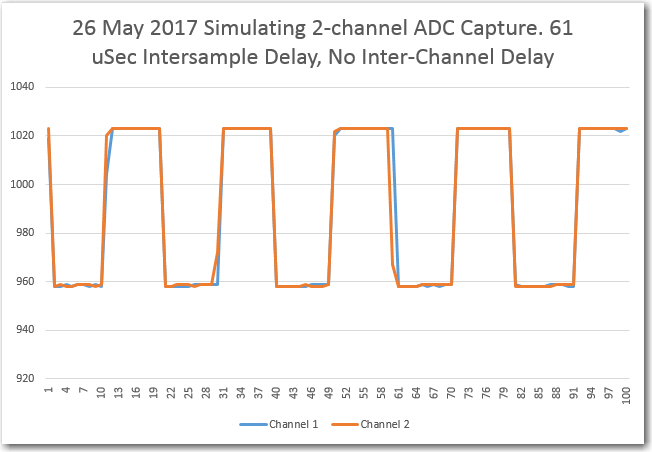
Next, I coded 500 iterations of a two-detector capture/sum operation, and got: “time required for 2-detector 500 analog read/store cycles = 15520”. So, about 31 uSec/iteration, or almost exactly twice the one-detector setup. A four-detector setup yielded a time of 30352 uSec for 500 iterations, or about 60.15 uSec/iteration. So, a 4-detector setup is possible, assuming the Uno 2KB memory constraint issue can be addressed successfully.
In summary:
- It takes about 15 uSec to read each sensor’s A/D value and either sum it or store it in an array
- A four-sensor setup can probably be accommodated, but only if the required summing arrays fit into available memory (not possible for Uno, but maybe for others.
- A loop delay value of 82 uSec results in almost exactly 20 samples/cycle.
Stay tuned
Frank