Posted 22 July 2017
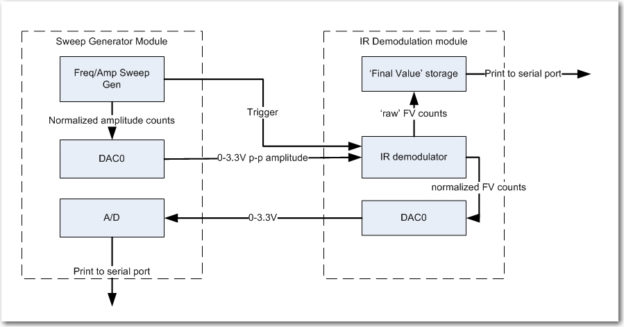
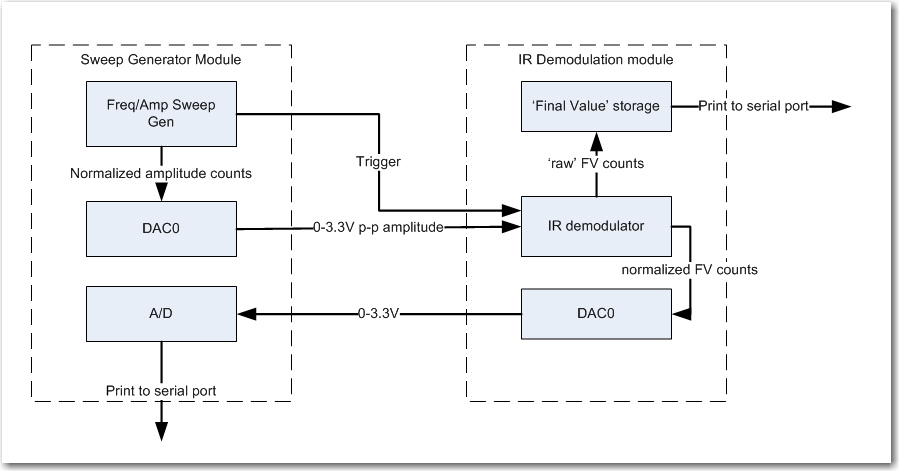
After getting the good news about the performance of my N-path filter for homing in on a 520Hz square-wave modulated IR beam, I still had two more significant tasks to accomplish; I still needed to extend the work to multiple (at least two) sensor channels for homing operation, and I needed to fully characterize the filter for frequency and amplitude response, and verify proper operation in the presence of ambient interference.
Second sensor channel:
As it turned out, add a second channel to the demodulator/filter algorithm was a piece of cake, as I didn’t have to bother with ‘array-izing’ everything – I just added a second set of input & output pins for the second channel, and a second set of variables. Basically it involved doing a global replace of ‘variable_name’ with ‘variable_name1’, and then copying ‘variable_name1’ to ‘variable_name2′ wherever it occurred. As an added bonus, the Teensy 3.5 has two DAC channels, so I could route the final value for channel2 to the second DAC pin for ’round-trip’ measurements with the sweep generator – nice
Frequency/Amplitude/Interference characterization:
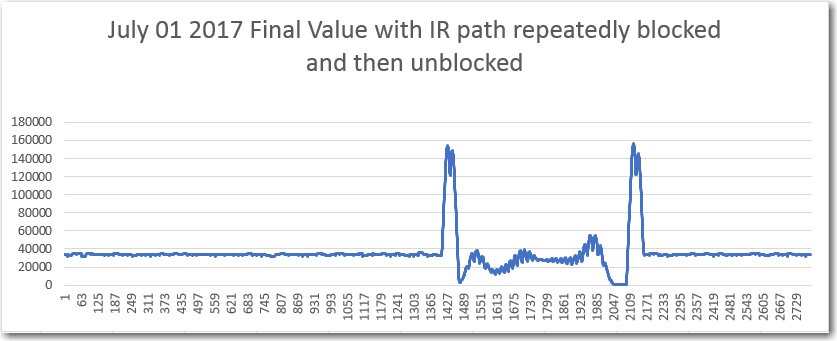
In wrapping my long and arduous journey toward a working 520Hz multi-sensor square-wave detector filter, I wanted to make a series of amplitude and frequency response plots for both banpass filter channels, and also figure out how to test for rejection of 60Hz & 60Hz harmonics.
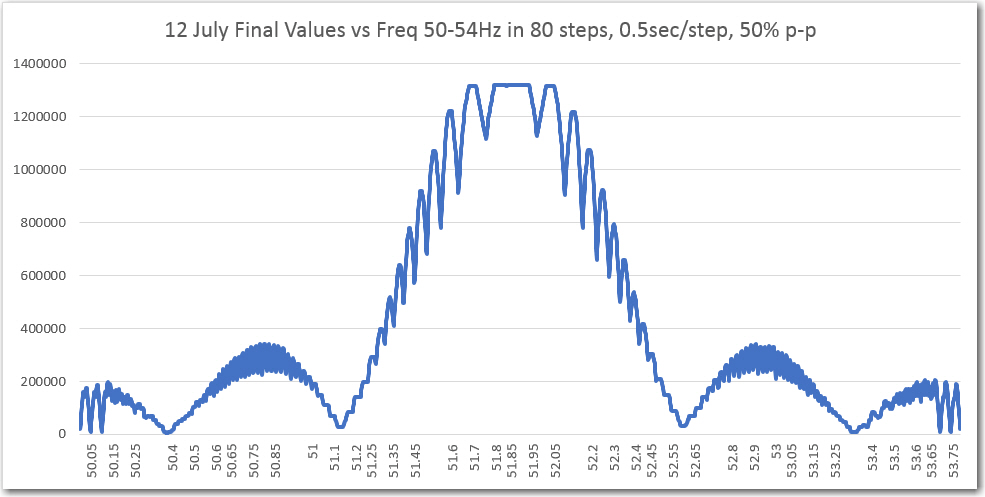
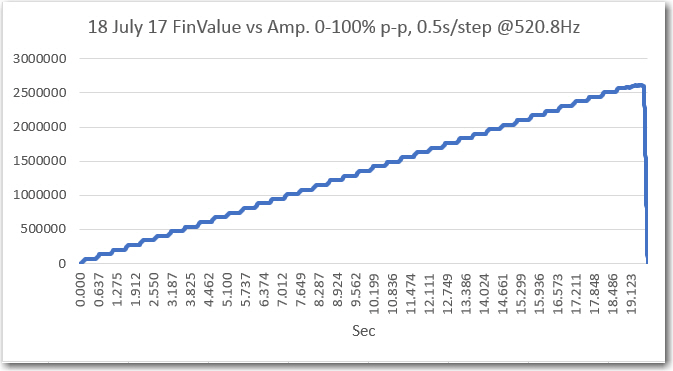
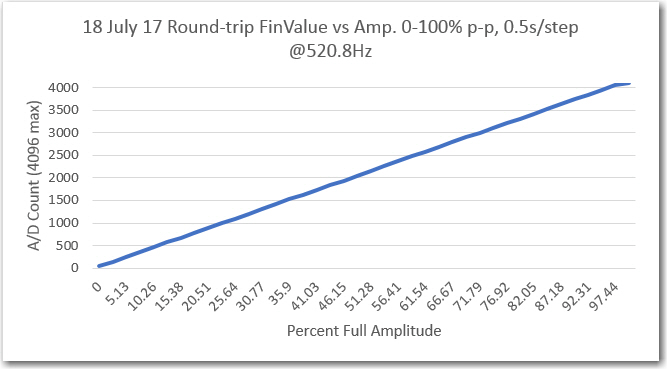
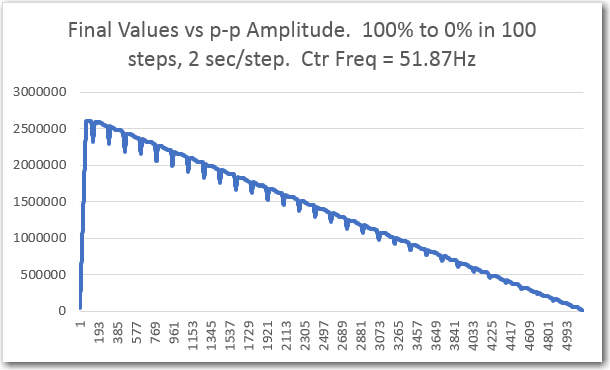
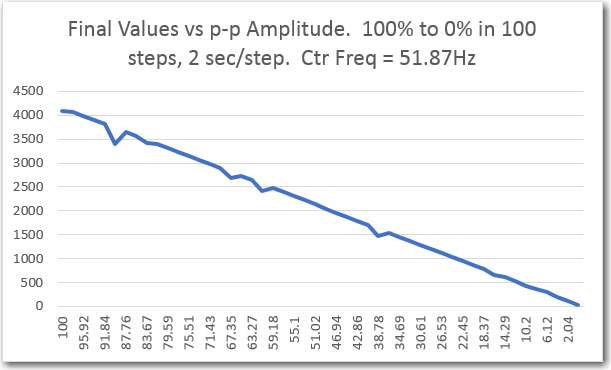
My initial amplitude sweep testing for channel 1 (original single channel) was very positive, as shown in the following plots:
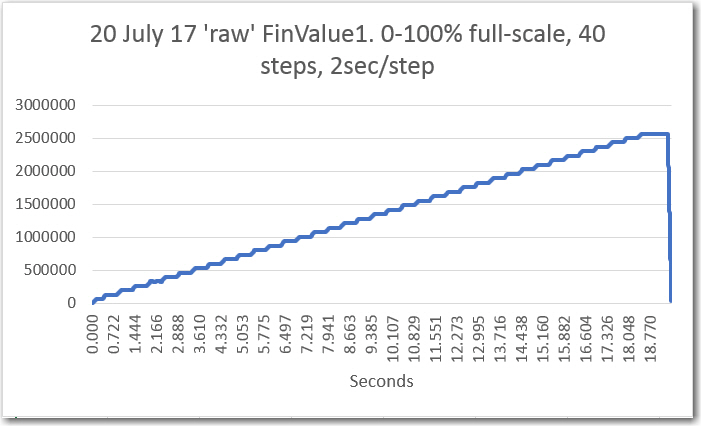
Channel 1 ‘raw’ amplitude response vs time
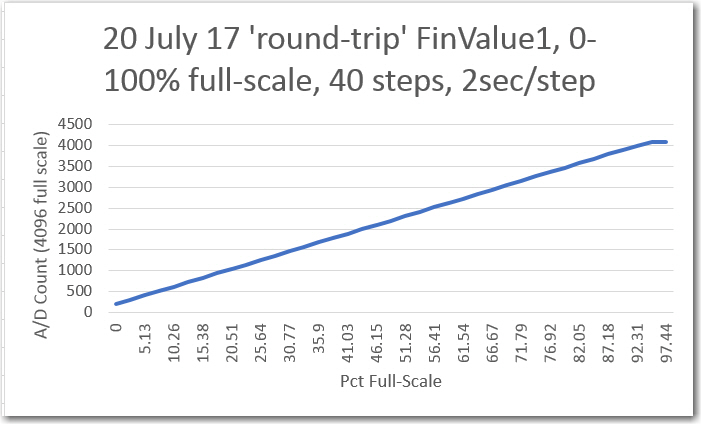
’round-trip (sweep gen -> IR Demod -> sweep gen) Channel 1 amplitude response vs input amplitude
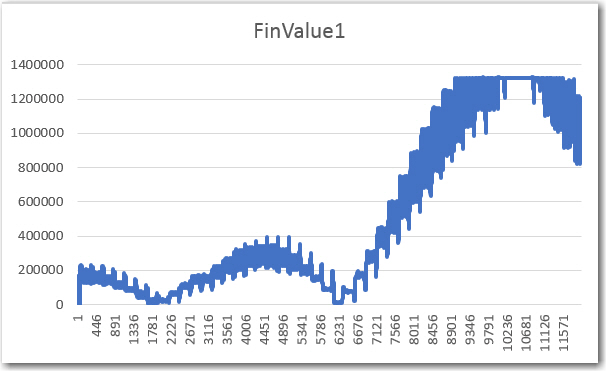
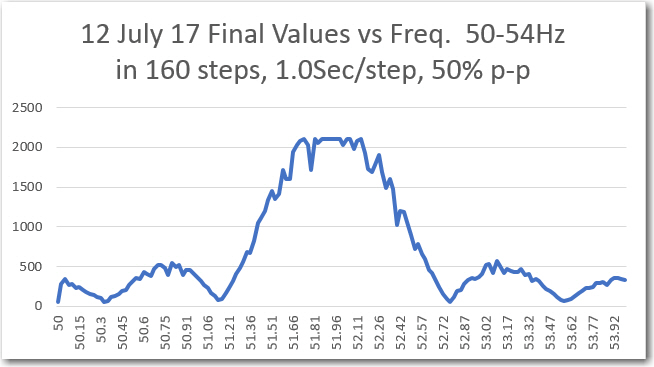
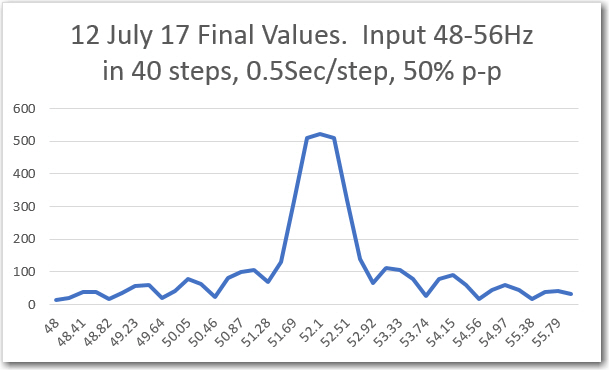
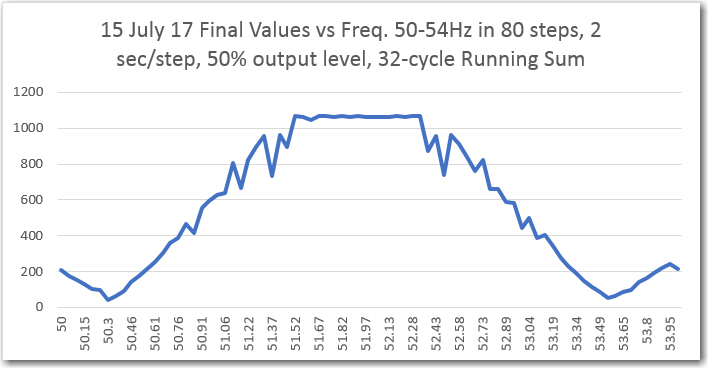
Channel1 Freq response
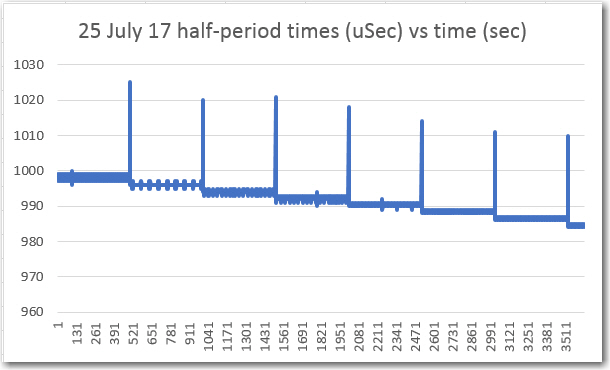
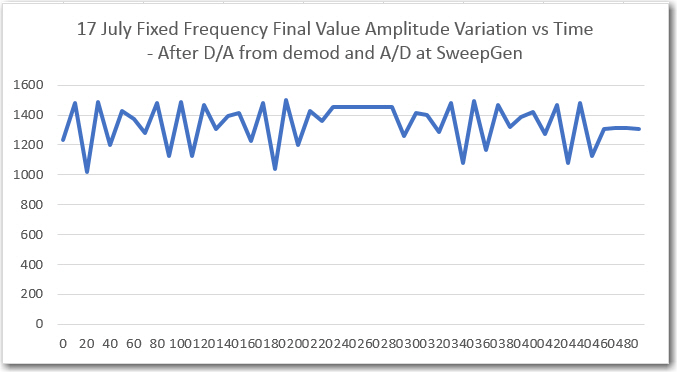
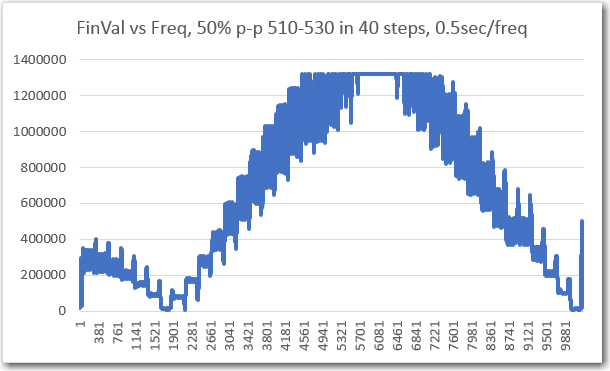
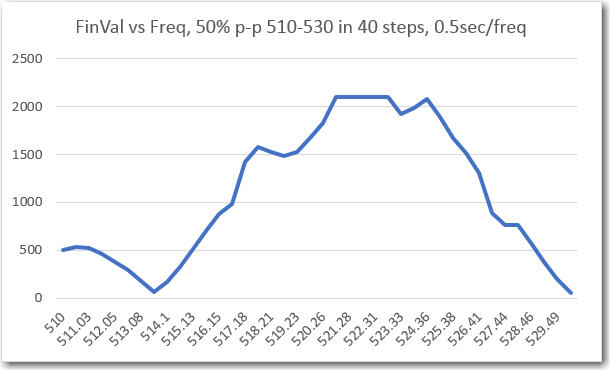
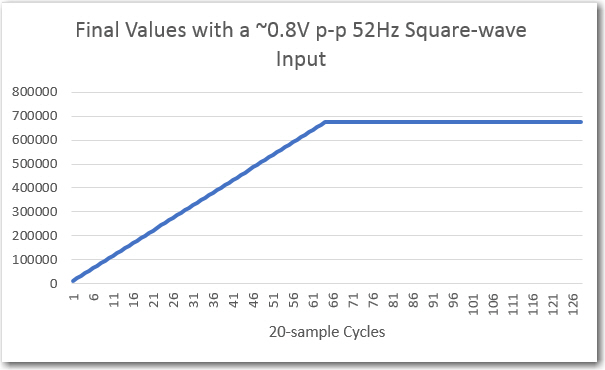
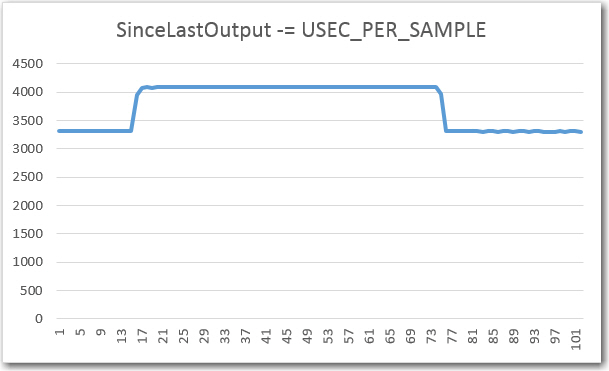
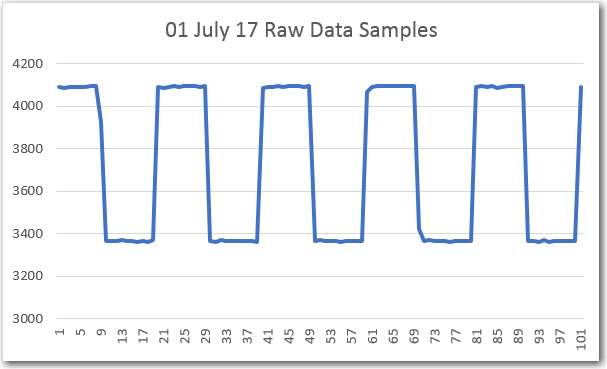
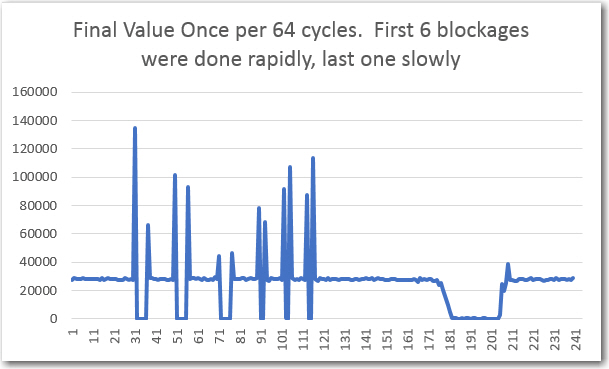
However, when I tried to run the frequency response curves, I ran into trouble (again!). As shown above, the plot was shifted significantly to the right, as if the demodulator’s frequency response had somehow shifted up in frequency. However, I knew from previous work that the demodulator center freq is 520.8Hz, so that couldn’t be the answer. The other possibility was that the sweep generator wasn’t producing the frequencies that I thought it was. Once I started thinking of this possibility, I remembered that a couple of days ago when I ran the very first fixed-amplitude response curves on the new-improved 520Hz demodulator, that I had been forced to tweak the sweep gen output freq to get the flat-line curve I was expecting. For convenience, I have repeated these plots below:
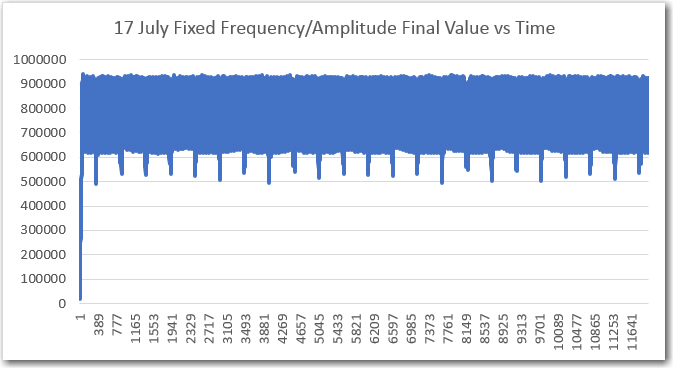
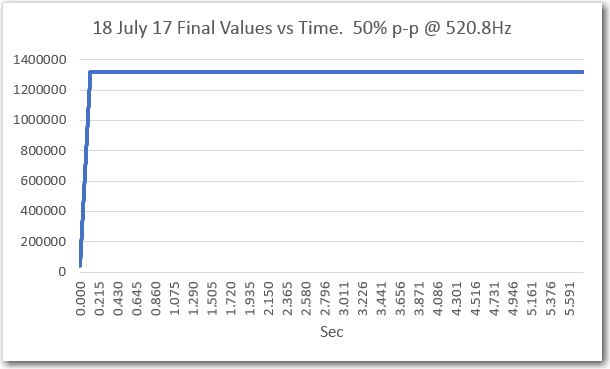
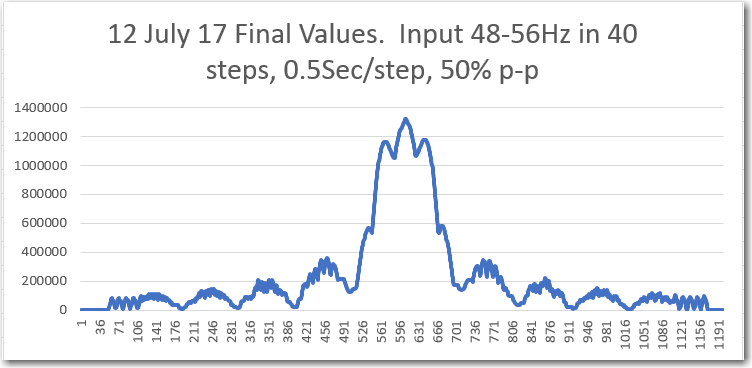
‘raw’ Final Values vs time, with fixed frequency, 50% p-p
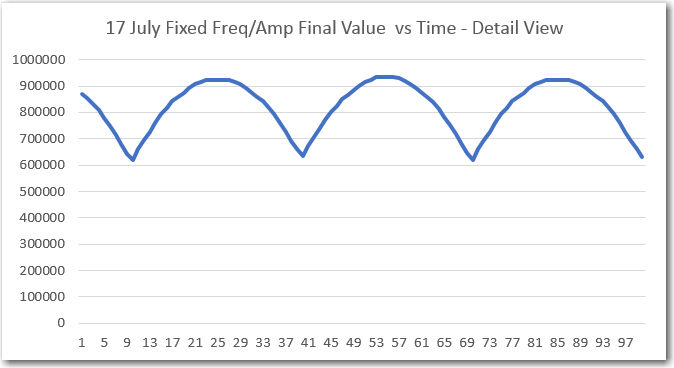
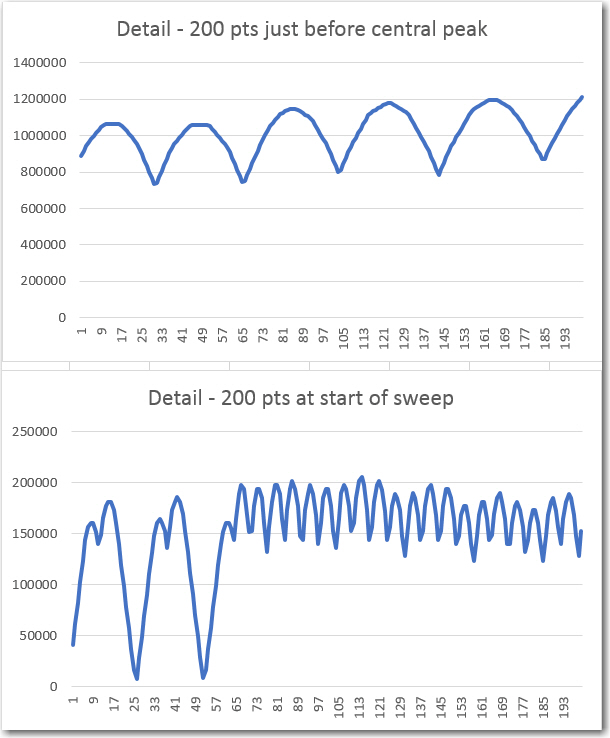
detail of ‘raw’ plot
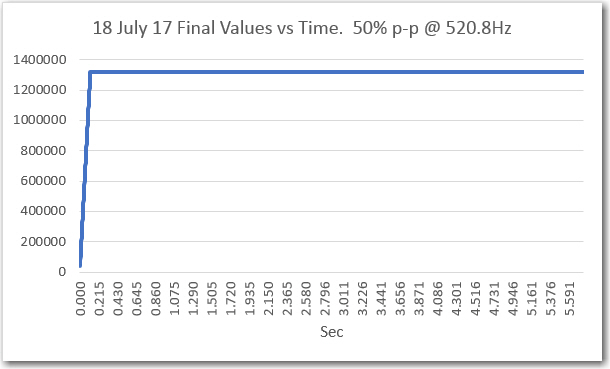
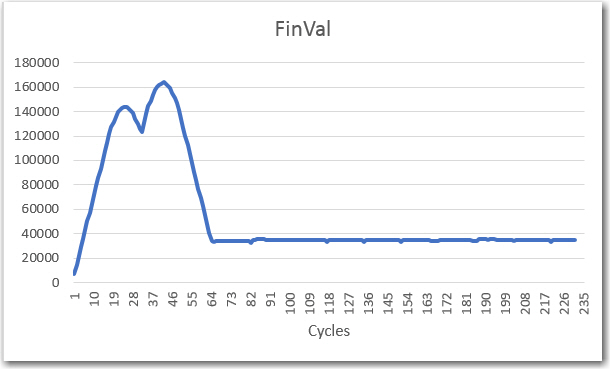
‘raw’ final values vs time after synching Tx & Rx frequencies
When I looked back into the sweep generator code, I found that its output frequency was set to 521.1Hz to produce a 520.8Hz output. At the time I didn’t think that was particularly egregious, but apparently is was a warning that I missed – oops!
So, now I embarked on yet another tangential project – this time to correct the frequency accuracy problems with the sweep generator module (which you might recall, was being used to test the IR demodulator, which in itself was a tangential project associated with the charging station project, which (you guessed it) was a tangential project in support of my Wall-E2 wall-following robot project. Talk about recursive! ;-).
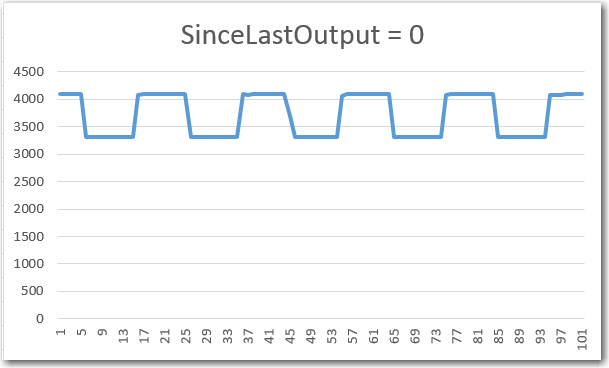
Anyway, my first attempt at a swept-frequency generation algorithm wasn’t all that brilliant – just using ‘delayMicros()’ calls to create the square-wave as shown below:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
{ float freqHz = FreqStart + i*freqstepHz; //Serial.print("Step "); Serial.print(i + 1); Serial.print(" Freq = "); Serial.println(freqHz); //compute required elapsed time for square wave transitions sinceLastTransition = 0.5e6 / freqHz; //output a square wave for the specified number of seconds long startMsec = millis(); long stopMsec = millis(); while (stopMsec - startMsec < 1000* SecPerFreqStep) { digitalWrite(SQWAVE_PIN, HIGH); analogWriteDAC0(DACoutHigh); digitalWrite(LED_PIN, HIGH); delayMicroseconds((int)sinceLastTransition); digitalWrite(SQWAVE_PIN, LOW); analogWriteDAC0(DACoutLow); digitalWrite(LED_PIN, LOW); delayMicroseconds((int)sinceLastTransition); stopMsec = millis(); //update the stop timer } |
In retrospect it was clear that this was never going to produce frequency-accurate square-waves because of the additional time taken by the read/write statements. Without compensating for this additional delay, the output freq would always be below the nominal value, which is what I was experiencing.
Next, I modified the algorithm to use Teensy’s ‘elapsedMicros’ data type, as shown below, and ran a series of tests to determine its frequency accuracy.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
if (sinceLastTransition >= HalfCycleMicroSec) { if (transNum < SINCELAST_ARRAY_LENGTH) { aSinceLast[transNum] = sinceLastTransition; //stored for later analysis } else { Serial.println("Sweep terminated early - aSinceLast overflow!"); DoSweepEnd(); //cleanup, offer to print, etc } sinceLastTransition -= HalfCycleMicroSec; //for most accurate timing transNum++; if (digitalRead(SQWAVE_PIN) == HIGH) { digitalWrite(SQWAVE_PIN, LOW); analogWriteDAC0(DACoutHigh * (1 - AmpPct / 100)); //level for this amp step digitalWrite(LED_PIN, LOW); } else { digitalWrite(SQWAVE_PIN, HIGH); //invert the output analogWriteDAC0(DACoutHigh); //level for this amp step digitalWrite(LED_PIN, HIGH); } //check for end of this step if (transNum >= numTransPerStep) { if (bIsFreqSweep) //change sqwv half-period { float curFreq = FreqStart + curStepNum*FreqStepVal; float nextFreq = curFreq + FreqStepVal; HalfCycleMicroSec = 5e5 / nextFreq; //print out Freq, Rx value Serial.print(curFreq);Serial.print("\t"); Serial.print(HalfCycleMicroSec, 6);Serial.print("\t"); Serial.print(analogRead(DEMOD_VALUE_READ_PIN)); Serial.println(); } else //change amplitude { AmpPct += AmpStepValPct; //stepVal = AmpPct; //print out amp val, Rx value Serial.print(AmpPct);Serial.print("\t"); Serial.print(analogRead(DEMOD_VALUE_READ_PIN)); Serial.println(); } transNum = 0; //start a new count curStepNum++; //increment the step count } //check for end of sweep //Serial.print("curstep/numsteps"); Serial.print(curStepNum); Serial.print("/"); Serial.println(numSteps); if (curStepNum > numSteps) { Serial.println("Sweep ended successfully..."); DoSweepEnd(); //cleanup, offer to print, etc } } }//loop() |
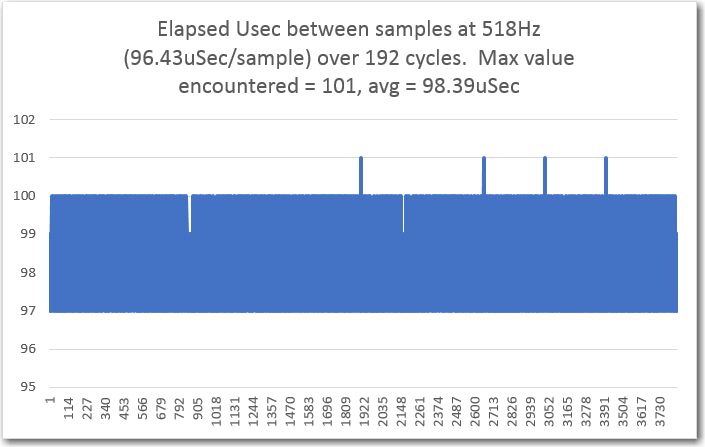
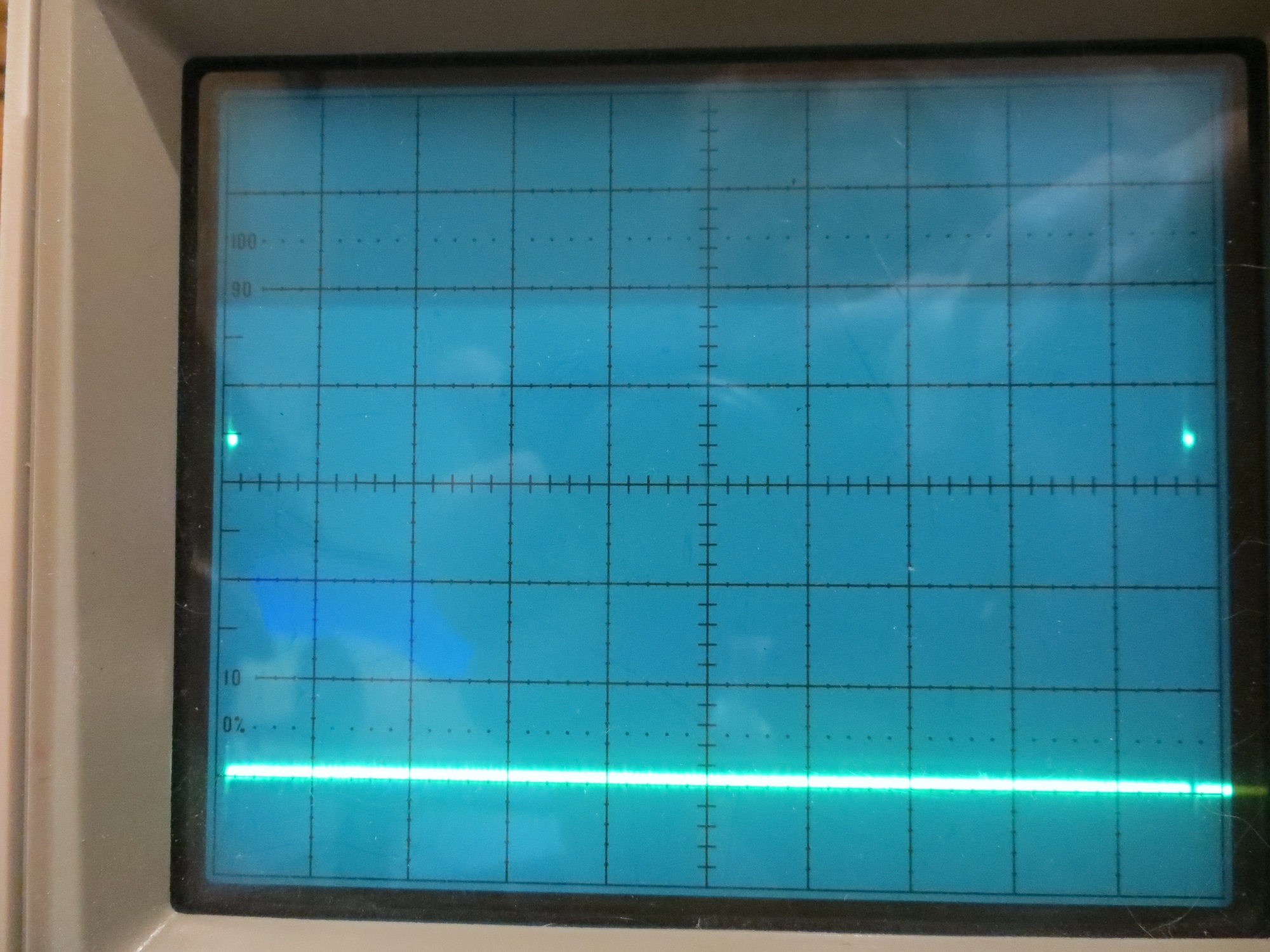
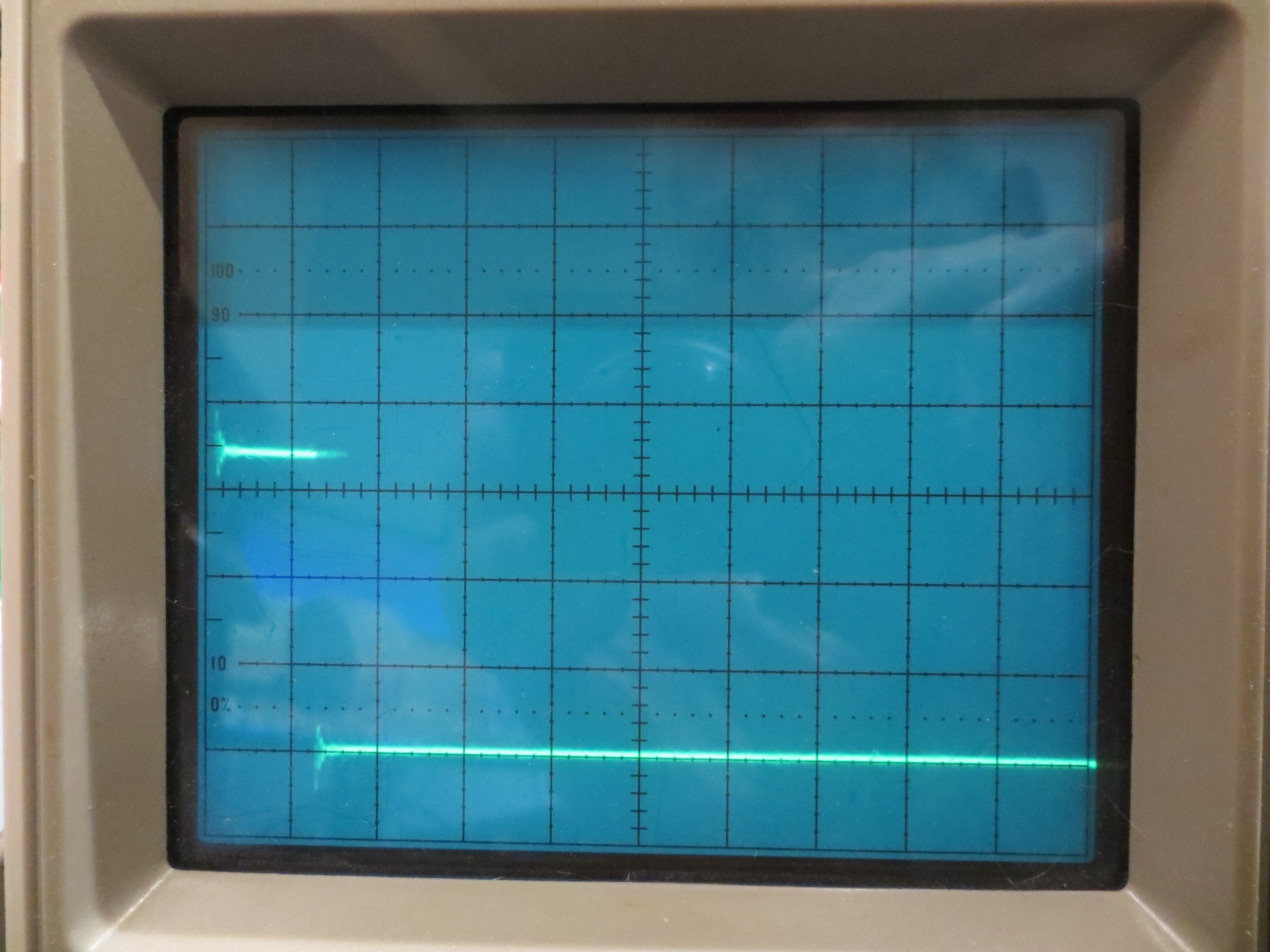
To test for frequency accuracy, I set the sweep generator to sweep from 501 to 531Hz with 50% output level and 5 sec/step. Then I measured the actual output frequency using my trusty Tektronix 2236 ‘scope with its built-in digital frequency readout. The results are shown below:
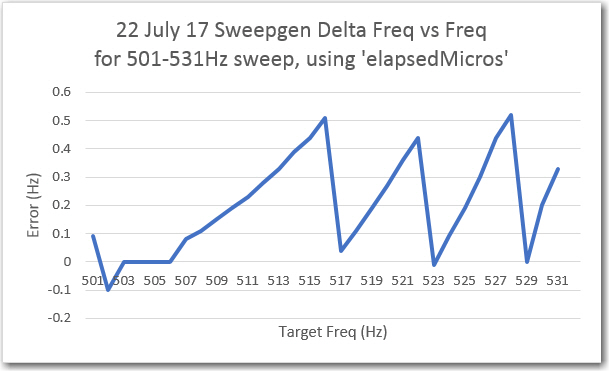
Frequency accuracy using the ‘elapsedMicros’ algorithm
This was OK, but not great, as it showed that the output frequency could be as much as 0.5Hz off from the expected value. After some web research (mostly on Paul Stoffregen’s wonderful Teensy forum), I decided to try the FrequencyTimer2 library described here. After implementing this in a separate test program, I ran the same frequency accuracy test as above, with the following results.
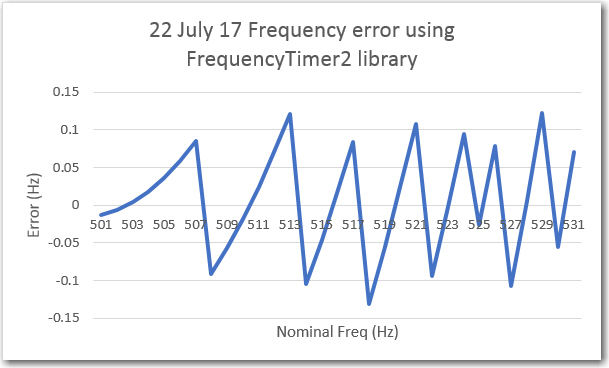
Frequency accuracy using the ‘FrequencyTimer2’ library
This was much better than the ‘elapsedMicros’ algorithm, but still not great; still greater than +/-0.1Hz deviation for some target frequencies.
Back to the web for more research, where I found the ‘IntervalTimer’ object described on this page. After modifying my test program to utilize this technique, I got the following results.
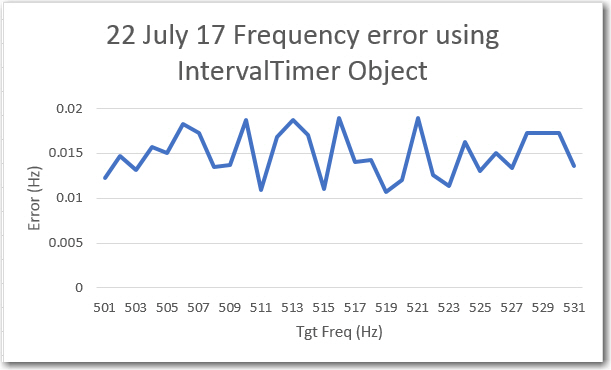
Frequency accuracy using the ‘IntervalTimer’ object
Wow! a lot better! Not only is the absolute error almost an order of magnitude less, the measured output frequency appears to be a constant 0.015Hz below (positive error) the target frequency. This leads me to believe that the frequency is probably right on the mark, and the error is in the measurement, not the timing. In any case, this technique is more than good enough for my puny little sweep generator! The complete test program used to generate these results is included below:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 |
// Create an IntervalTimer object IntervalTimer myTimer; const int ledPin = LED_BUILTIN; // the pin with a LED const int OUTPUT_PIN = 33; void setup(void) { pinMode(ledPin, OUTPUT); pinMode(OUTPUT_PIN, OUTPUT); Serial.begin(115200); Serial.println("Freq\tTimerVal"); for (size_t i = 501; i <= 531; i++) { float period = 1e6 / i; Serial.println(i);Serial.print("\t"); Serial.println(period); myTimer.begin(blinkLED, period/2); delay(5000); myTimer.end(); } //myTimer.begin(blinkLED, 150000); // blinkLED to run every 0.15 seconds } // The interrupt will blink the LED, and keep // track of how many times it has blinked. int ledState = LOW; volatile unsigned long blinkCount = 0; // use volatile for shared variables // functions called by IntervalTimer should be short, run as quickly as // possible, and should avoid calling other functions if possible. void blinkLED(void) { if (ledState == LOW) { ledState = HIGH; //blinkCount = blinkCount + 1; // increase when LED turns on } else { ledState = LOW; } digitalWrite(ledPin, ledState); digitalWrite(OUTPUT_PIN, ledState); } // The main program will print the blink count // to the Arduino Serial Monitor void loop(void) { //unsigned long blinkCopy; // holds a copy of the blinkCount // to read a variable which the interrupt code writes, we // must temporarily disable interrupts, to be sure it will // not change while we are reading. To minimize the time // with interrupts off, just quickly make a copy, and then // use the copy while allowing the interrupt to keep working. //noInterrupts(); //blinkCopy = blinkCount; //interrupts(); //Serial.print("blinkCount = "); //Serial.println(blinkCopy); //delay(100); } |
Before implementing the ‘IntervalTimer’ technique in my mainline sweep generator program, I re-ran the frequency sweep from 501 to 531Hz, with the following results.
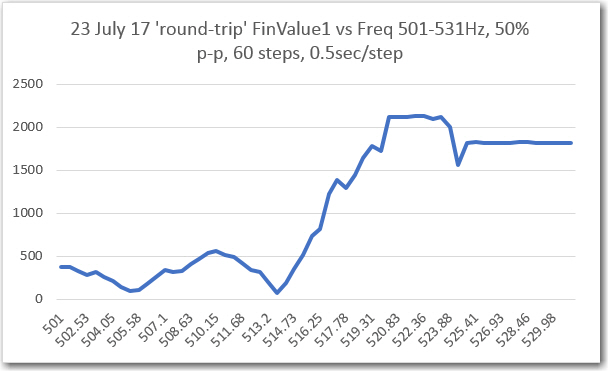
’round-trip’ freq sweep results before implementing the ‘IntervalTimer’ technique
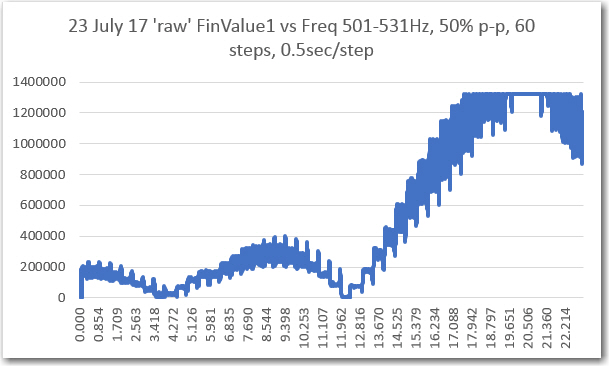
‘raw’ freq sweep results before implementing the ‘IntervalTimer’ technique
After implementing the new ‘IntervalTimer’ technique, I ran the sweeps again with nothing else changed, with the following results.
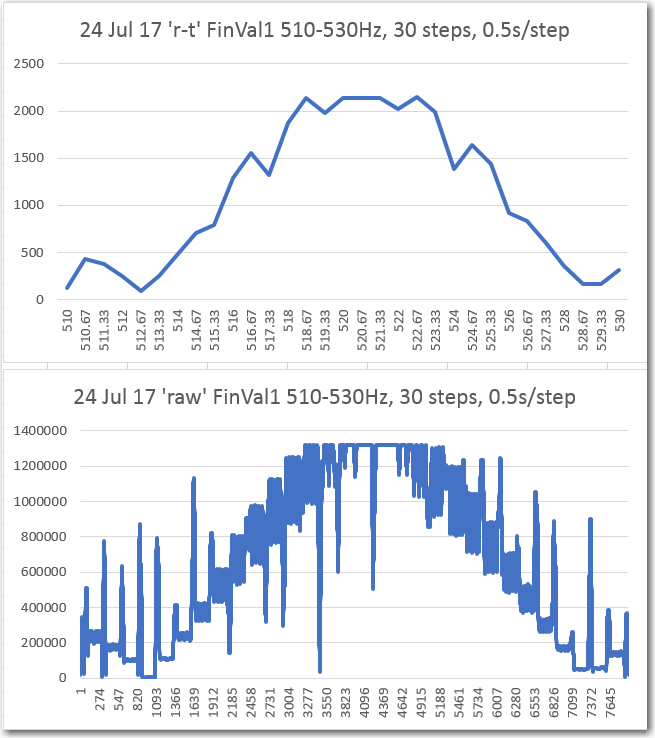
‘Round-trip’ and ‘raw’ FinalValue vs Frequency, with IntervalTimer technique
As can be seen from the above plots, they are nicely centered vs frequency, but the ‘raw’ plot has a lot of clearly ‘bad’ data – huge positive and negative excursions from the expected value.
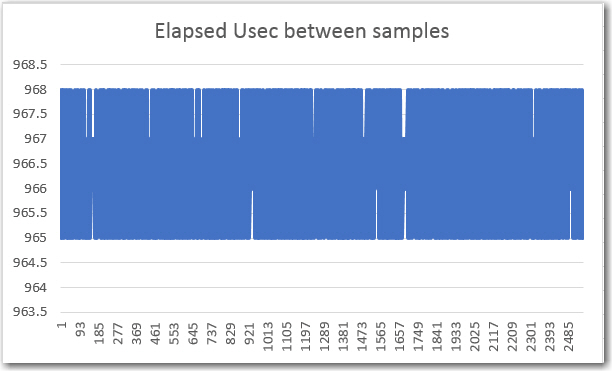
This situation led me down yet another rabbit-hole – what is causing these erroneous results? It appears that the bad data occurs at the beginning and the end of each 0.5 second frequency step – what could be causing that? After some thought, I decided to instrument the Interrupt Service Routine (ISR) that generates the square-wave transitions. As the following plot shows, there is a clear ‘glitch’ at the beginning of the first transition for each frequency step.
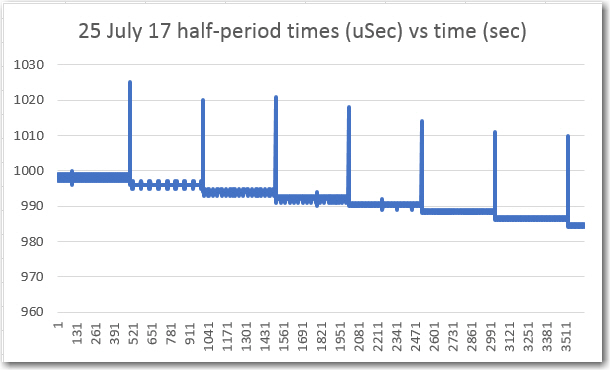
Square-wave transition times vs time using the IntervalTimer technique
Looking at the code that generates the sweep (shown below), it appears that the problem occurs because the IntervalTimer object must be destroyed (with ‘myTimer.end()’ and then re-created (with ‘myTimer.begin()’) with the new transition time. This inevitably causes the first transition of the next frequency step to be considerably off from nominal, and I don’t think there is anything I can do about it – bummer! 🙁
|
1 2 3 4 5 6 7 8 9 10 11 |
for (int i = 0; i <= FreqSteps; i++) { float freqHz = FreqStart + i*freqstepHz; //Serial.print("Step "); Serial.print(i + 1); Serial.print(" Freq = "); Serial.println(freqHz); //compute required elapsed time for square wave transitions HalfCycleMicroSec = 0.5e6 / freqHz; myTimer.begin(SqwvGen, HalfCycleMicroSec); delay(SecPerFreqStep*1000); myTimer.end(); } |
So, it appears that my choices for accurate frequency generation are:
- Use the ‘elapsedMicros()’ feature, with it’s inherent 0.5Hz max frequency error (due to rounding – this might be tweakable)
- Use the ‘FrequencyTimer2’ library. This results in about 0.1Hz max error (again, possibly tweakable). Unfortunately, this technique requires that the output occur on a specific pin, which means I can’t output different levels without external hardware
- Use the ‘IntervalTimer’ interrupt technique, which is very fast and very accurate. Unfortunately, as noted above, it also produces artifacts in the output spectra.
As I mentioned at the start of this post, this entire project is about three or four levels deep in the ‘tangential’ stack. The very last thing I wanted was yet another tangential project to learn the strengths/weaknesses of the various timing methods so I can implement the one with the best strength/weakness ratio, but yet here I am – arghhhh!
Stay tuned!
Frank